江苏省泰州医药高新区2020年数学中考二模试卷
试卷更新日期:2020-08-18 类型:中考模拟
一、选择题
-
1. 的值等于( )A、3 B、-3 C、±3 D、2. 如果3x=4y(y≠0),那么下列比例式中正确的是( )A、 B、 C、 D、3. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 4. 若点 , 在一次函数 的图象上,则代数式 的值为( )A、1 B、2 C、4 D、55. 某几何体的三视图如图,则该几何体是( )
4. 若点 , 在一次函数 的图象上,则代数式 的值为( )A、1 B、2 C、4 D、55. 某几何体的三视图如图,则该几何体是( ) A、长方体 B、圆柱 C、球 D、正三棱柱6. 如图,点A,B,C,D在⊙O上,弦AD的延长线与弦BC的延长线相交于点E.用①AB是⊙O的直径,②CB=CE,③AB=AE中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
A、长方体 B、圆柱 C、球 D、正三棱柱6. 如图,点A,B,C,D在⊙O上,弦AD的延长线与弦BC的延长线相交于点E.用①AB是⊙O的直径,②CB=CE,③AB=AE中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( ) A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
7. 4的算术平方根是 , 9的平方根是 , ﹣27的立方根是 .8. 若多边形的内角和是外角和的2倍,则该多边形是边形.9. 人体血液中,红细胞的直径约为0.000 007 7m.用科学记数法表示0.000 007 7m是.10. 已知关于 的方程 有两个不相等的实数根,则 的取值范围是 .11. 圆锥的底面半径长为5,将其侧面展开后得到一个半圆,则该半圆的半径长是 .12. 如图,身高1.8米的小石从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为米.
 13. 用一组a,b的值说明命题“如果 ,那么 ”是错误的,这组值可以是.14. 一张三角形纸片ABC,其中∠C=90?,AC=6,BC=8.小静同学将纸片做两次折叠:第一次使点A落在C处,折痕记为m;然后将纸片展平做第二次折叠,使点A落在B处,折痕记为n.则m,n的大小关系是.15. 如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为.
13. 用一组a,b的值说明命题“如果 ,那么 ”是错误的,这组值可以是.14. 一张三角形纸片ABC,其中∠C=90?,AC=6,BC=8.小静同学将纸片做两次折叠:第一次使点A落在C处,折痕记为m;然后将纸片展平做第二次折叠,使点A落在B处,折痕记为n.则m,n的大小关系是.15. 如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为.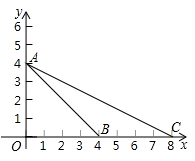 16. 如图,在正方形 中, , 、 是对角线 上的两个动点(点 靠近点 ),且 , 是正方形四边上的任意一点.若 是等边三角形,则 AE的长为 .
16. 如图,在正方形 中, , 、 是对角线 上的两个动点(点 靠近点 ),且 , 是正方形四边上的任意一点.若 是等边三角形,则 AE的长为 .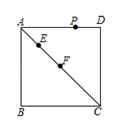
三、解答题
-
17.(1)、计算: ;(2)、计算(x+y)2-y(2x+y).18. 已知 , 且 ,求代数式 的值.19. 已知⊙O及⊙O上一点P,过点P作⊙O的切线.
小明设计了如下尺规作法:
①连接OP,以点P为圆心,OP长为半径画弧交⊙O于点A;
②连接OA,延长OA到B,使AB=OA,作直线PB.则直线即为所求作.
(1)、请证明小明作法的正确性;(2)、请你自己再设计一种尺规作图方法(保留痕迹,不要证明). 20. 一只不透明的袋子中装有3个白球、1个红球,这些球除颜色外都相同,搅匀后从中任意摸出2个球.请通过列表或画树状图的方法计算下列事件的概率:(1)、摸出的2个球都是白球;(2)、摸出的2球是一个红球和一个白球.21. 2020年新冠肺炎疫情发生以来,我市广大在职党员积极参与社区防疫工作,助力社区坚决打赢疫情防控阻击战.其中,A社区有500名在职党员,为了解本社区2月—3月期间在职党员参加应急执勤的情况,A社区针对执勤的次数随机抽取50名在职党员进行调查,并对数据进行了整理、描述和分析,下面给出了部分信息.
20. 一只不透明的袋子中装有3个白球、1个红球,这些球除颜色外都相同,搅匀后从中任意摸出2个球.请通过列表或画树状图的方法计算下列事件的概率:(1)、摸出的2个球都是白球;(2)、摸出的2球是一个红球和一个白球.21. 2020年新冠肺炎疫情发生以来,我市广大在职党员积极参与社区防疫工作,助力社区坚决打赢疫情防控阻击战.其中,A社区有500名在职党员,为了解本社区2月—3月期间在职党员参加应急执勤的情况,A社区针对执勤的次数随机抽取50名在职党员进行调查,并对数据进行了整理、描述和分析,下面给出了部分信息.次数x/次
频数
频率
0 ≤x< 10
8
0.16
10≤x< 20
10
0.20
20≤x< 30
16
b
30≤x< 40
a
0.24
x≥ 40
4
0.08
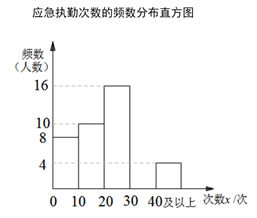
其中,应急执勤次数在20≤x< 30这一组的数据是:
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
请根据所给信息,解答下列问题:
(1)、 = , =;(2)、请补全频数分布直方图;(3)、随机抽取的50名在职党员参加应急执勤次数的中位数是;(4)、请估计2月—3月期间A社区在职党员参加应急执勤的次数不低于30次的约有__人.22. 某市水果批发欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时,其它主要参考数据如下:运输工具
途中平均速度(千米/时)
运费(元/千米)
装卸费用(元)
火车
100
15
2000
汽车
80
20
900
(1)、如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.(总支出包含损耗、运费和装卸费用)(2)、如果A市与B市之间的距离为S千米,你若是A市水果批发部门的经理,要想将这种水果运往B市销售,试分析以上两种运输工具中选择哪种运输方式比较合算呢?23. 如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为48°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i= ,且D、M、E、C、N、B、A在同一平面内,M、E、C、N在同一条直线上.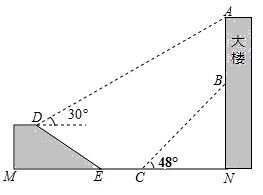
(参考数据:sin48°≈ ,tan48°≈ )
(1)、求BN的长度;(2)、求条幅AB的长度(结果保留根号).24. 如图,直线 与函数 的图象交于点 ,与 轴交于点 .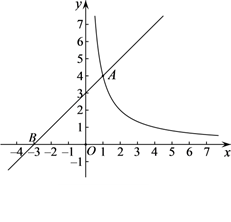 (1)、求 , 的值;(2)、过动点 作平行于 轴的直线,交函数 的图象于点 ,交直线 于点 .
(1)、求 , 的值;(2)、过动点 作平行于 轴的直线,交函数 的图象于点 ,交直线 于点 .①当 时,求线段 的长;
②若 ,结合函数的图象,直接写出 的取值范围.
25. 如图,在矩形ABCD中,AB=3,BC=4,点E在AD上,BE与AC交于点F. (1)、若AC⊥BE,求AE的长 ;(2)、设△DEF和△DCF的面积分别为S1和S2 , 当AE=m时,求S1:S2;(3)、当AE的长是多少时,△DCF是等腰三角形?26. 二次函数 的图象经过点 (0,-4)和 (-2,2).
(1)、若AC⊥BE,求AE的长 ;(2)、设△DEF和△DCF的面积分别为S1和S2 , 当AE=m时,求S1:S2;(3)、当AE的长是多少时,△DCF是等腰三角形?26. 二次函数 的图象经过点 (0,-4)和 (-2,2).
 (1)、求 的值,并用含 的式子表示 ;(2)、求证:此抛物线与 轴有两个不同交点;(3)、当 时,若二次函数满足 随 的增大而减小,求 的取值范围;(4)、直线 上有一点 ( ,5),将点 向右平移4个单位长度,得到点 ,若抛物线与线段 只有一个公共点,求 的取值范围.
(1)、求 的值,并用含 的式子表示 ;(2)、求证:此抛物线与 轴有两个不同交点;(3)、当 时,若二次函数满足 随 的增大而减小,求 的取值范围;(4)、直线 上有一点 ( ,5),将点 向右平移4个单位长度,得到点 ,若抛物线与线段 只有一个公共点,求 的取值范围.