湖北省武汉市武昌区2020年数学中考模拟试卷
试卷更新日期:2020-08-18 类型:中考模拟
一、选择题
-
1. 2的相反数是( )A、 B、 C、2 D、2. 若式子 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、3. 下列说法正确的是( )A、打开电视机,它正在播广告是必然事件 B、“明天降水概率80%”,是指明天有80%的时间在下雨 C、方差越大数据的波动越大,方差越小数据的波动越小 D、在抽样调查过程中,样本容量越小,对总体的估计就越准确4. 下列四个图案中,轴对称图形的个数是( )个
 A、1 B、2 C、3 D、45. 如图是由五个完全相同的小正方体组成的几何体,这个几何体的俯视图是( )
A、1 B、2 C、3 D、45. 如图是由五个完全相同的小正方体组成的几何体,这个几何体的俯视图是( )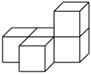 A、
A、 B、
B、 C、
C、 D、
D、 6. 公元前 世纪,古希腊数学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即“阻力 阻力臂 动力 动力臂”.若现在已知某一杠杆的阻力和阻力臂分别为 和 ,则动力 (单位: )关于动力臂 (单位: )的函数图象大致是( )
6. 公元前 世纪,古希腊数学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即“阻力 阻力臂 动力 动力臂”.若现在已知某一杠杆的阻力和阻力臂分别为 和 ,则动力 (单位: )关于动力臂 (单位: )的函数图象大致是( ) A、
A、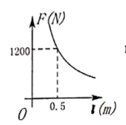 B、
B、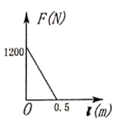 C、
C、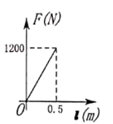 D、
D、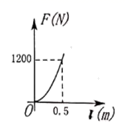 7. 小明投掷一次骰子,向上一面的点数记为 ,再投掷一次骰子,向上一面的点数记为 ,这样就确定点 的一个坐标 ,那么点 落在双曲线 上的概率为( )A、 B、 C、 D、8. 如图,反比例函数 的图象分别与矩形 的边 , 相交于点 , ,与对角线 交于点 ,以下结论:
7. 小明投掷一次骰子,向上一面的点数记为 ,再投掷一次骰子,向上一面的点数记为 ,这样就确定点 的一个坐标 ,那么点 落在双曲线 上的概率为( )A、 B、 C、 D、8. 如图,反比例函数 的图象分别与矩形 的边 , 相交于点 , ,与对角线 交于点 ,以下结论: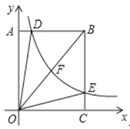
①若 与 的面积和为2,则 ;
②若 点坐标为 , ,则 ;
③图中一定有 ;
④若点 是 的中点,且 ,则四边形 的面积为18.
其中一定正确个数是( )
A、1 B、2 C、3 D、49. 如图,正方形 的边长为1,点 是 边上的一点,将 沿着 折叠得 .若 , 恰好都与正方形 的中心 为圆心的 相切,则折痕 的长为( )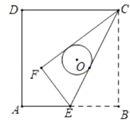 A、 B、 C、 D、10. 如图所示,将形状、大小完全相同的“ ”和线段按照一定规律摆成下列图形,第1幅图形中“ ”的个数为 ,第2幅图形中“ ”的个数为 ,第3幅图形中“ ”的个数为 , ,以此类推,则 的值为( )
A、 B、 C、 D、10. 如图所示,将形状、大小完全相同的“ ”和线段按照一定规律摆成下列图形,第1幅图形中“ ”的个数为 ,第2幅图形中“ ”的个数为 ,第3幅图形中“ ”的个数为 , ,以此类推,则 的值为( )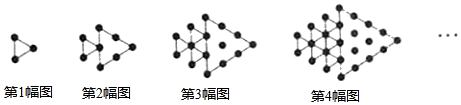 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
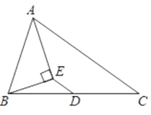
11. 计算 的结果是.12. 在一次考试中,某小组8名同学的成绩(单位:分)分别是:7,10,8,8,10,7,9,7,则这组数据的中位数是.13. 化简: 的结果是.14. 如图, 平分 , 于 , , ,那么 的度数为.
 15. 我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形 ,正方形 ,正方形 的面积分别为 , , ,若 ,则 的值是.
15. 我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形 ,正方形 ,正方形 的面积分别为 , , ,若 ,则 的值是.
三、解答题
-
16. 计算: .17. 如图, , ,求证: .
 18. 某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
18. 某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:成绩 (分)
频数
频率
20
16
0.08
0.15

请你根据以上的信息,回答下列问题:
(1)、 , ;(2)、在扇形统计图中,“成绩 满足 ”对应扇形的圆心角的度数是;(3)、若将得分转化为等级,规定: 评为 , 评为 , 评为 , 评为 .这次全校参加竞赛的学生约有人参赛成绩被评为“ ”.19. 定义:顶点都在网格点上的四边形叫做格点四边形,端点都在网格点上的线段叫做格点线.如图1,在正方形网格中,格点线DE、CE将格点四边形ABCD分割成三个彼此相似的三角形.请你在图2、图3中分别画出格点线,将阴影四边形分割成三个彼此相似的三角形. 20. 如图, 的直径 ,直线 与 相切于点 ,连接 ,过点 作 于点 , 交 于点 , .
20. 如图, 的直径 ,直线 与 相切于点 ,连接 ,过点 作 于点 , 交 于点 , .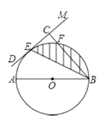 (1)、求线段 的长;(2)、求图中阴影部分的面积.21. 某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如下表:
(1)、求线段 的长;(2)、求图中阴影部分的面积.21. 某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如下表:售价(元/件)
200
210
220
230
…
月销量(件)
200
180
160
140
…
已知该运动服的进价为每件150元.
(1)、售价为 元,月销量为 件;①求 关于 的函数关系式;
②若销售该运动服的月利润为 元,求 关于 的函数关系式,并求月利润最大时的售价;
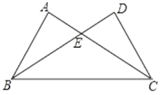
(2)、由于运动服进价降低了 元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则 的值是多少?22. 中, 是 的中点,点 在 上(点 不与 重合),过点 的直线交 于 ,交射线 于点 ,设 , .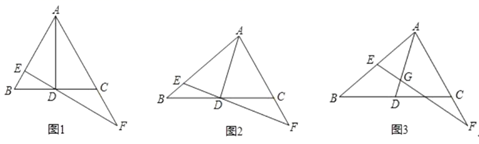 (1)、如图1,若 为等边三角形,点 与 重合, ,求证: ;(2)、如图2,若点 与 重合,求证: ;(3)、如图3,若 , , ,直接写出 的值.23. 已知抛物线的顶点 ,经过点 ,与 轴分别交于 , 两点.
(1)、如图1,若 为等边三角形,点 与 重合, ,求证: ;(2)、如图2,若点 与 重合,求证: ;(3)、如图3,若 , , ,直接写出 的值.23. 已知抛物线的顶点 ,经过点 ,与 轴分别交于 , 两点.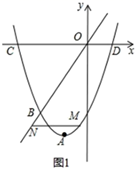
 (1)、求该抛物线的解析式;(2)、如图1,点 是抛物线上的一个动点,且在直线 的下方,过点 作 轴的平行线与直线 交于点 ,当 取最大值时,求点 的坐标;(3)、如图2, 轴交 轴于点 ,点 是抛物线上 , 之间的一个动点,直线 , 与 分别交于 , ,当点 运动时.
(1)、求该抛物线的解析式;(2)、如图1,点 是抛物线上的一个动点,且在直线 的下方,过点 作 轴的平行线与直线 交于点 ,当 取最大值时,求点 的坐标;(3)、如图2, 轴交 轴于点 ,点 是抛物线上 , 之间的一个动点,直线 , 与 分别交于 , ,当点 运动时.①直接写出 的值;
②直接写出 的值.