河南省南召县2020年数学中考二模试卷

试卷更新日期：2020-08-18 类型：中考模拟

进入出卷网下载

一、选择题

1. $- \frac{1}{2}$ 的绝对值是（）

A、-2 B、 $- \frac{1}{2}$ C、2 D、 $\frac{1}{2}$

查看试题解析
2. 下列图形中，是轴对称图形，但不是中心对称图形的是（）

A、 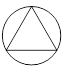B、 C、 D、

查看试题解析
3. 下列各式计算正确的是（）

A、2a²＋3a²＝5a⁴ B、(－2ab)³＝－6ab³ C、(3a＋b)(3a－b)＝9a²－b² D、a³·(－2a)＝－2a³

查看试题解析
4. 如图，一个圆柱体在正方体上沿虚线从左向右平移，平移过程中不变的是（）

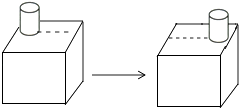A、主视图 B、左视图 C、俯视图 D、主视图和俯视图

查看试题解析
5. 学校团委组织“抗疫情，献爱心”网上捐款活动，九年级一班学生捐款情况如下表：

捐款金额（元）

5

10

20

50

人数（人）

10

13

12

15

则学生捐款金额的中位数、众数分别是（）

A、13、15 B、10、20 C、15、50 D、20、50

查看试题解析
6. 关于x的一元二次方程x²+ax﹣1=0的根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
7. 如图，在△AEF中，尺规作图如下：分别以点E，点F为圆心，大于 $\frac{1}{2}$ EF的长为半径作弧，两弧相交于G，H两点，作直线GH，交EF于点O，连接AO，则下列结论正确的是（　　）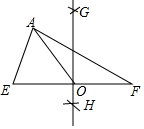

A、AO平分∠EAF B、AO垂直平分EF C、GH垂直平分EF D、GH平分AF

查看试题解析
8. 甲盒子中装有3个乒乓球，分别标号为1，2，3；乙盒子中装有2个乒乓球，分别标号为1，2.现从每个盒子中随机取出1个球，则取出的两球标号之和为4的概率是（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
9. 如图，AB是半圆O的直径，半径OC⊥AB于点O，点D是 $\overset{⌢}{B C}$ 的中点，连接CD，OD，BD，下列四个结论：①AC∥OD；②CD＝BD；③△ODE∽△CAE；④∠ADC＝∠BOD.其中正确结论的序号是（）

A、①②③④ B、①②④ C、②③ D、①④

查看试题解析
10. 如图（1），直线l的解析式为y＝－x＋b，且与x轴，y轴分别交于点A，B，平行于直线l的直线m从原点O出发，沿x轴的正方向以每秒1个单位长度的速度运动，与x轴，y轴分别交于点C，D，运动时间为t秒（0≤t≤b），将△OCD沿着直线m翻折得到△ECD.若△ECD和△OAB的重合部分的面积为S（设t＝0或b时，S＝0），且S与t之间的函数关系的图象如图（2）所示，则图象中的最高点P的坐标是（）

A、（ $\frac{8}{3}$ ，3） B、（3，3） C、（ $\frac{8}{3}$ ， $\frac{8}{3}$ ） D、（3， $\frac{8}{3}$ ）

查看试题解析

二、填空题

11. 计算： ${(- 2020)}^{0} + {(- 2 + 1)}^{- 2} =$ .

查看试题解析
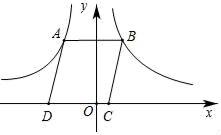
12. 不等式组 ${\begin{array}{l} 2 x - 1 \leq 1 \\ - \frac{1}{2} x < 1 \end{array}$ 的整数解的为.

查看试题解析
13. 如图，点B是反比例函数y＝ $\frac{2}{x}$ （x＞0）的图象上任意一点，AB∥x轴并交反比例函数y＝﹣ $\frac{3}{x}$ （x＜0）的图象于点A，以AB为边作平行四边形ABCD，其中C、D在x轴上，则平行四边形ABCD的面积为.

查看试题解析
14. 已知如图，扇形AOB的圆心角∠AOB＝90°，OA＝4，点C、点E分别是OB、OA的中点，CD⊥OB，EF⊥OA，则阴影部分面积为.

查看试题解析
15. 如图，在矩形ABCD中，AD＝6，AB＝4，以AD为直径在矩形内作半圆，点E为半圆上的一动点（不与A、D重合），连接DE、CE，当△DEC为等腰三角形时，DE的长为.

查看试题解析

三、解答题

16. 先化简，再求值： $\frac{a}{a^{2} - 4} \div \frac{a^{2} - 3 a}{a + 2} - \frac{1}{2 - a}$ ，其中a与2，3构成 $Δ A B C$ 的三边，且a为整数.

查看试题解析
17. “停课不停学，学习不延期！”某市教育局为了解初中学生疫情期间在家学习时对一些学习方式的喜好情况，通过微信采用电子问卷的方式随机调查了部分学生（电子调查表如图所示），并根据调查结果绘制了如下尚不完整的统计图，

根据以上统计图，解答下列问题：

(1)、本次接受调查的学生共有人；

(2)、补全条形统计图；

(3)、扇形统计图中，扇形B的圆心角的度数是度；

(4)、若该市约有16万初中生，请估计喜欢自学（选择选项C和D）的学生人数.

查看试题解析
18. 如图（1）是小明家购买的一款台灯，现忽略支架的粗细，得到它的侧面简化示意图如图（2）所示.支架AB与桌面的夹角为80°，支架AB与支架BC的夹角为100°，CD平行于桌面，支架AB，BC的长度均为20cm.求灯泡顶端D到桌面的距离DE.（结果精确到1cm.参考数据：sin80°≈0.98，cos80°≈0.17，tan80°≈5.67，sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）

查看试题解析
19. 如图，AB为⊙O的直径，点D是AB下方圆上的一点，点C是优弧AD的中点，过点B作⊙O的切线BE交AC的延长线于点E，连接OC，OD，CB，BD.

(1)、求证：BD∥OC；

(2)、当AB＝6时，完成填空：
①当BE＝时，四边形ODBC是菱形；

②当BE＝时，S_△_BCE＝ $\frac{1}{4}$ S_△_ABC.

查看试题解析

20. 某数学兴趣小组对函数

y = | \frac{2}{3} x^{2} - \frac{4}{3} x - 2 |

的图象和性质进行了研究，探究过程如下.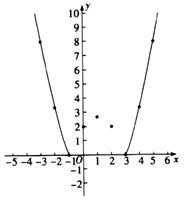

(1)、自变量x的取值范围是全体实数，x与y的几组对应值列表如下.

x	…	-3	-2	-1	0	1	2	3	4	5	…
y	…	8	m	0	2	n	2	0	$\frac{10}{3}$	8	…

其中，m= ， n=；

(2)、根据上表数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请补全函数图象的剩余部分；

(3)、进一步探究函数图象发现：

①函数图象与x轴有个交点；

②方程 $| \frac{2}{3} x^{2} - \frac{4}{3} x - 2 | = 1$ 有个实数根；

③当关于x的方程 $| \frac{2}{3} x^{2} - \frac{4}{3} x - 2 | = p$ 有3个实数根时，p的值是.

查看试题解析

21. 为响应国家“垃圾分类进校园”的号召，某校准备购买新的分类垃圾箱进行更换，已知购买5个A类垃圾箱和4个B类垃圾箱需花费1600元，购买3个A类垃圾箱的费用恰好等于购买4个B类垃圾箱的费用.

(1)、求购买一个A类垃圾箱和一个B类垃圾箱各需多少元；

(2)、该校计划用不超过9000元的经费购买A类和B类垃圾箱共50个，其中A类垃圾箱的数量不低于25个，则本次可以选择的方案有几种；

(3)、在(2)的条件下哪种方案的费用最低，最低费用是多少元.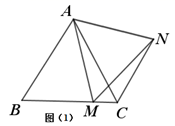

查看试题解析
22.

(1)、问题提出
如图（1），在等边三角形ABC中，点M是BC上的任意一点（不含端点B、C），连接AM，以AM为边作等边三角形AMN，连接CN，则∠ACN＝°.

(2)、类比探究
如图（2），在等边三角形ABC中，点M是BC延长线上的任意一点（不含端点C），其他条件不变，（1）中的结论还成立吗？请说明理由.

(3)、拓展延伸
如图（3），在等腰三角形ABC中，BA＝BC，点M是BC上的任意一点（不含端点B、C），连接AM，以AM为边作等腰三角形AMN，使AM＝MN，连接CN.添加一个条件，使得∠ABC＝∠ACN仍成立，写出你所添加的条件，并说明理由.

查看试题解析
23. 如图，抛物线y＝x²＋bx＋c与x轴交于A（－1，0），与y轴交于C（0，－2）；直线 $y = \frac{3}{4} x + \frac{3}{4}$ 经过点A且与抛物线交于另一点B $(\frac{11}{4} ， \frac{45}{16})$ .
（

(1)、直接写出抛物线的解析式；

(2)、如图（1），点M是抛物线上A，B两点间的任一动点，MN⊥AB于点N，试求出MN的最大值，并求出MN最大时点M的坐标；

(3)、如图（2），连接AC，已知点P的坐标为（2，1），点Q为对称轴左侧的抛物线上的一动点，过点Q作QF⊥x轴于点F，是否存在这样的点Q，使得∠FQP＝∠CAO.若存在，请直接写出点Q的坐标；若不存在，请说明理由.

查看试题解析

捐款金额（元）	5	10	20	50
人数（人）	10	13	12	15