上海市虹口区2019-2020学年高二下学期数学期末考试试卷
试卷更新日期:2020-08-18 类型:期末考试
一、单选题
-
1. 设 , 是两个不同的平面,m是直线且 .“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件2. 设 、 分别是椭圆 ( )的左、右焦点,过 的直线 与椭圆E相交于A、B两点,且 ,则 的长为( )A、 B、1 C、 D、3. 方程为 的曲线,给出下列四个结论:
① 关于 轴对称;② 关于坐标原点对称;③ 关于y轴对称; ④ , ;
以上结论正确的个数是( )
A、1 B、2 C、3 D、44. 如图,正方体 的棱长为1,P为 的中点,Q为线段 上的动点,过点A、P、Q的平面截该正方体所得的截面记为S,给出下列三个结论:
① 当 时,S为四边形;
② 当 时,S为等腰梯形;
③ 当 时,S的面积为 ;
以上结论正确的个数是( )
A、0 B、1 C、2 D、35. 正方体 的棱长为1,P为 的中点,Q为线段 上的动点,三棱锥 的体积记为 ,三棱锥 的体积记为 ,则以下结论正确的是( )A、 B、 C、 D、 与 的大小关系不能确定二、填空题
-
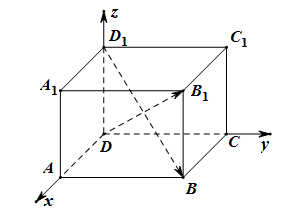
6. 若 ( 是虚数单位)是关于x的实系数方程 的一个根,则 等于.7. 已知直线 , ,若 ∥ ,则实数a的值等于.8. 在平面直角坐标系中, , ,若 ,则P点的轨迹方程为.9. 在长方体 中, , ,则直线 与 所成的角的大小等于.10. 过抛物线 的焦点且与对称轴垂直的弦长为 .11. 如图,以长方体 的顶点 为坐标原点,过D的三条棱所在的直线为坐标轴,建立空间直角坐标系,若 的坐标为 ,则 的坐标为.
 12. 一个袋中装有9个形状大小完全相同的球,球的编号为1,2, ,9,随机摸出两个球,则两个球编号之和为奇数的概率是.(结果用分数表示)13. 已知 ,则 的值为.14. 棱长为a的正方体 的顶点A到截面 的距离等于.15. 在平面直角坐标系 中,直线 ( 为参数)与圆 ( 为参数)相切,则实数a的值为.16. 我们知道:用平行于圆锥母线的平面(不过顶点)截圆锥,则平面与圆锥侧面的交线是抛物线一部分,如图,在底面半径和高均为2的圆锥中, 、 是底面圆O的两条互相垂直的直径,E是母线 的中点,已知过 与 的平面与圆锥侧面的交线是以W为顶点的圆锥曲线的一部分,则该圆锥曲线的焦点到其准线的距离等于.
12. 一个袋中装有9个形状大小完全相同的球,球的编号为1,2, ,9,随机摸出两个球,则两个球编号之和为奇数的概率是.(结果用分数表示)13. 已知 ,则 的值为.14. 棱长为a的正方体 的顶点A到截面 的距离等于.15. 在平面直角坐标系 中,直线 ( 为参数)与圆 ( 为参数)相切,则实数a的值为.16. 我们知道:用平行于圆锥母线的平面(不过顶点)截圆锥,则平面与圆锥侧面的交线是抛物线一部分,如图,在底面半径和高均为2的圆锥中, 、 是底面圆O的两条互相垂直的直径,E是母线 的中点,已知过 与 的平面与圆锥侧面的交线是以W为顶点的圆锥曲线的一部分,则该圆锥曲线的焦点到其准线的距离等于.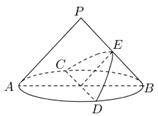 17. 已知点 ,圆 上的两个点 、 满足 ( ),则 的最大值为.18. 抛物线 的焦点到准线的距离等于.19. 求圆 上的点到直线 的距离的最大值.
17. 已知点 ,圆 上的两个点 、 满足 ( ),则 的最大值为.18. 抛物线 的焦点到准线的距离等于.19. 求圆 上的点到直线 的距离的最大值.三、解答题
-
20. 已知i是虚数单位,复数 满足方程 ( ),求实数a、b的值.21. 已知双曲线 ( ),直线l与 交于P、Q两点.(1)、若点 是双曲线 的一个焦点,求 的渐近线方程;(2)、若点P的坐标为 ,直线 的斜率等于1,且 ,求双曲线 的渐近线方程.22. 已知三棱锥 (如图一)的平面展开图(如图二)中, 为边长等于 的正方形,△ 和△ 均为正三角形,在三棱锥 中,
 (1)、求证: ;(2)、求 与平面 所成的角的大小;(3)、求二面角 的大小.23. 焦距为 的椭圆 ( ),如果满足“ ”,则称此椭圆为“等差椭圆”.(1)、如果椭圆 ( )是“等差椭圆”,求 的值;(2)、如果椭圆 ( )是“等差椭圆”,过 作直线 与此“等差椭圆”只有一个公共点,求此直线的斜率;(3)、椭圆 ( )是“等差椭圆”,如果焦距为12,求此“等差椭圆”的方程;(4)、对于焦距为12的“等差椭圆”,点A为椭圆短轴的上顶点,P为椭圆上异于A点的任一点,Q为P关于原点O的对称点(Q也异于A),直线 、 分别与x轴交于M、N两点,判断以线段 为直径的圆是否过定点?说明理由.24. 定义空间点到几何图形的距离为:这一点到这个几何图形上各点距离中最短距离.(1)、在空间,求与定点O距离等于1的点所围成的几何体的体积和表面积;(2)、在空间,线段 (包括端点)的长等于1,求到线段 的距离等于1的点所围成的几何体的体积和表面积;(3)、在空间,记边长为1的正方形 区域(包括边界及内部的点)为 ,求到 距离等于1的点所围成的几何体的体积和表面积.
(1)、求证: ;(2)、求 与平面 所成的角的大小;(3)、求二面角 的大小.23. 焦距为 的椭圆 ( ),如果满足“ ”,则称此椭圆为“等差椭圆”.(1)、如果椭圆 ( )是“等差椭圆”,求 的值;(2)、如果椭圆 ( )是“等差椭圆”,过 作直线 与此“等差椭圆”只有一个公共点,求此直线的斜率;(3)、椭圆 ( )是“等差椭圆”,如果焦距为12,求此“等差椭圆”的方程;(4)、对于焦距为12的“等差椭圆”,点A为椭圆短轴的上顶点,P为椭圆上异于A点的任一点,Q为P关于原点O的对称点(Q也异于A),直线 、 分别与x轴交于M、N两点,判断以线段 为直径的圆是否过定点?说明理由.24. 定义空间点到几何图形的距离为:这一点到这个几何图形上各点距离中最短距离.(1)、在空间,求与定点O距离等于1的点所围成的几何体的体积和表面积;(2)、在空间,线段 (包括端点)的长等于1,求到线段 的距离等于1的点所围成的几何体的体积和表面积;(3)、在空间,记边长为1的正方形 区域(包括边界及内部的点)为 ,求到 距离等于1的点所围成的几何体的体积和表面积.