河南省南阳市新野县2020年数学中考一模试卷
试卷更新日期:2020-08-18 类型:中考模拟
一、选择题
-
1. 我国能制造芯片的最小工艺水平是16纳米,已知1纳米 米,用科学记数法将16纳米表示为( )A、 B、 C、 D、2. 直线 ,一块含 角的直角三角板,如图放置, ,则 等于( )
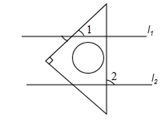 A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 一个几何体的三视图如图所示,则这个几何体是( )
A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 一个几何体的三视图如图所示,则这个几何体是( ) A、
A、 B、
B、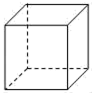 C、
C、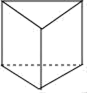 D、
D、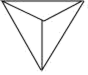 5. 一元二次方程 根的情况是( )A、有两个相等实根 B、有两个不相等实根 C、无实根 D、无法判定6. 根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( )
5. 一元二次方程 根的情况是( )A、有两个相等实根 B、有两个不相等实根 C、无实根 D、无法判定6. 根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( ) A、扇形统计图能反映各部分在总体中所占的百分比 B、每天阅读30分钟以上的居民家庭孩子超过50% C、每天阅读1小时以上的居民家庭孩子占20% D、每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°7. 如图,平行四边形 中, , .以点 为圆心,适当长为半径面弧,交 于点 ,交 于点 ,再分别以点 、 为圆心,大于 的长为半径面弧,两弧相交于点 ,射线 交 的延长线于点 ,则 的长是( )
A、扇形统计图能反映各部分在总体中所占的百分比 B、每天阅读30分钟以上的居民家庭孩子超过50% C、每天阅读1小时以上的居民家庭孩子占20% D、每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°7. 如图,平行四边形 中, , .以点 为圆心,适当长为半径面弧,交 于点 ,交 于点 ,再分别以点 、 为圆心,大于 的长为半径面弧,两弧相交于点 ,射线 交 的延长线于点 ,则 的长是( )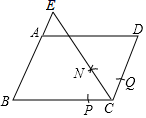 A、 B、 C、1 D、28. 已知二次函数 ,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是( )A、有最大值﹣1,有最小值﹣2 B、有最大值0,有最小值﹣1 C、有最大值7,有最小值﹣1 D、有最大值7,有最小值﹣29. 在平面直角坐标系中,将边长为1的正方形 绕点 顺时针旋转 后得到正方形 ,依此方式,绕点 连续旋转 次得到正方形 ,那么点 的坐标是( )
A、 B、 C、1 D、28. 已知二次函数 ,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是( )A、有最大值﹣1,有最小值﹣2 B、有最大值0,有最小值﹣1 C、有最大值7,有最小值﹣1 D、有最大值7,有最小值﹣29. 在平面直角坐标系中,将边长为1的正方形 绕点 顺时针旋转 后得到正方形 ,依此方式,绕点 连续旋转 次得到正方形 ,那么点 的坐标是( )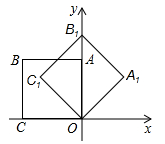 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 计算: .11. 不等式组 的最小正整数解为 .12. 某商场举办抽奖活动,规则如下:在不透明的袋子中有2个红球和2个黑球,这些球除颜色外都相同,顾客每次摸出一个球,若摸到红球,则获得1份奖品,若摸到黑球,则没有奖品,如果小芳有两次摸球机会(摸出后不放回),小芳获得2份奖品的概率为 .13. 如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为.
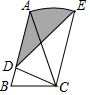 14. 如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为.
14. 如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为.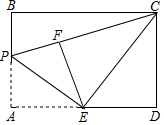
三、解答题
-
15. 先化简,再求值: ,从 中的整数中选一个作为 的值,求出这个代数式的值.16. 红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数
人数
班级
60
70
80
90
100
1班
0
1
6
2
1
2班
1
1
3
1
3班
1
1
4
2
2
分析数据:
平均数
中位数
众数
1班
83
80
80
2班
83
3班
80
80
根据以上信息回答下列问题:
(1)、请直接写出表格中 的值;(2)、比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;(3)、为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级新生共570人,试估计需要准备多少张奖状?17. 如图, 是 的直径,点 是 上一点,点 是 的中点,过点 作 的切线,与 、 的延长线分别交于点 、 ,连接 .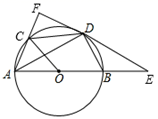 (1)、求证: ;(2)、直接回答:①已知 ,当 为何值时, ?
(1)、求证: ;(2)、直接回答:①已知 ,当 为何值时, ?②连接 、 、 ,当 等于多少度时,四边形 是菱形?
18. 某数学兴趣小组要测量实验大楼上的显示屏 的高度,如图①所示,在地面上的点 处测得大楼显示屏的顶端 点的仰角为 ,底端 点的仰角为 ,从 开始向前走20米到达 处,测得顶端 的仰角为 ,如图②所示, 、 、 在一条直线上,求显示屏 的高度约为多少米?(精确到1米)
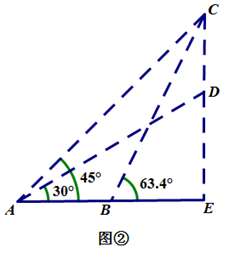
(参考数据: , , , , )
19. 开学前夕,某文具店准备购进A、B两种品牌的文具袋进行销售,若购进A品牌文具袋和B品牌文具袋各5个共花费125元,购进A品牌文具袋3个和B品牌文具袋各4个共花费90元.(1)、求购进A品牌文具袋和B品牌文具袋的单价;(2)、若该文具店购进了A,B两种品牌的文具袋共100个,其中A品牌文具袋售价为12元,B品牌文具袋售价为23元,设购进A品牌文具袋x个,获得总利润为y元.①求y关于x的函数关系式;
②要使销售文具袋的利润最大,且所获利润不超过进货价格的40%,请你帮该文具店设计一个进货方案,并求出其所获利润的最大值.
20. 某班数学兴趣小组对函数 的图象和性质将进行了探究,探究过程如下,请补充完整.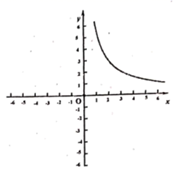 (1)、自变量 的取值范围是除0外的全体实数, 与 的几组对应值列表如下:
(1)、自变量 的取值范围是除0外的全体实数, 与 的几组对应值列表如下:…
1
2
3
6
…
…
1
2
6
1
3
2
1
…
其中, .
(2)、根据上表数据,在如图所示的平面直角坐标系中描点并画出了函数图象的一部分,请画出该函数图象的另一部分.(3)、观察函数图象,写出一条函数性质.(4)、进一步探究函数图象发现:①函数图象与 轴交点情况是 , 所以对应方程 的实数根的情况是.
②方程 有个实效根;
③关于 的方程 有2个实数根, 的取值范围是.
21.(1)、问题发现:如图1,在等边 中,点 为 边上一动点, 交 于点 ,将 绕点 顺时针旋转 得到 ,连接 .则 与 的数量关系是 , 的度数为.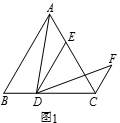 (2)、拓展探究:如图2,在 中, , ,点 为 边上一动点, 交 于点 ,当∠ADF=∠ACF=90°时,求 的值.
(2)、拓展探究:如图2,在 中, , ,点 为 边上一动点, 交 于点 ,当∠ADF=∠ACF=90°时,求 的值.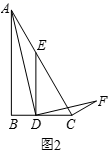 (3)、解决问题:如图3,在 中, ,点 为 的延长线上一点,过点 作 交 的延长线于点 ,直接写出当 时 的值.
(3)、解决问题:如图3,在 中, ,点 为 的延长线上一点,过点 作 交 的延长线于点 ,直接写出当 时 的值.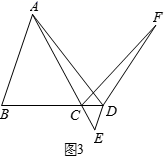 22. 如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
22. 如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.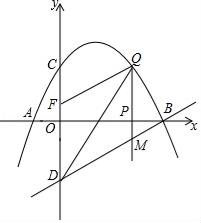 (1)、求该抛物线所表示的二次函数的表达式;(2)、已知点F(0, ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?(3)、点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、求该抛物线所表示的二次函数的表达式;(2)、已知点F(0, ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?(3)、点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.