江苏省泰兴市宁界2020年数学中考模拟试卷

试卷更新日期：2020-08-18 类型：中考模拟

进入出卷网下载

一、选择题

1. PM2.5是指大气中直径小于或等于2.5μm（0.0000025m）的颗粒物，含有大量有毒、有害物质，也称可入肺颗粒物．将0.0000025用科学记数法表示为（）

A、25×10^﹣⁷ B、2.5×10^﹣⁶ C、0.25×10^﹣⁵ D、2.5×10⁶

查看试题解析
2. 下列图形中既是轴对称图形，又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 下列方程中，没有实数根的是（　　）

A、2x+3＝0 B、x²﹣1＝0 C、 $\frac{2}{x + 1} = 1$ D、x²+x+1＝0

查看试题解析
4. 可能性是10%的事件在100试验中发生的次数为m，可能性是30%的事件在100试验中发生的次数为n，则（　　）

A、m>n B、m=n C、m<n D、无法比较m与n的大小

查看试题解析
5. 将点P（－2，3）向右平移3个单位得到点P₁ ，点P₂与点P₁关于原点对称，则P₂的坐标是（）

A、（－5，－3） B、（1，－3） C、（－1，－3） D、（5，－3）

查看试题解析
6. 如图，直线l与⊙O相切于点A，M是⊙O上的一个动点，MH⊥l，垂足为H.若⊙O的半径为1，则MA-MH的最大值为（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析

二、填空题

7. 若 $\frac{a}{2} = \frac{b}{3} = \frac{c}{4}$ ，则 $\frac{a + b}{b + 2 c}$ ＝.

查看试题解析
8. 因式分解：xy³－x³y＝.

查看试题解析
9. 如果一个正多边形的中心角为45°，那么这个正多边形的边数是.

查看试题解析
10. 二次函数y＝ax²+bx+2的图象经过点（-1，0），则代数式2a-2b的值.

查看试题解析
11. 一元二次方程x²+3x+1＝0的两根分别为x₁、x₂ ，则x₁+x₂+x₁x₂＝.

查看试题解析
12. 八年级某同学6次数学小测验的成绩分别为：80分，85分，95分，95分，95分，100分，则该同学这6次成绩的中位数是.

查看试题解析
13. 在平面直角坐标系xOy中，点A（m，n)在双曲线 $y = - \frac{2}{x}$ 上，点A关于y轴的对点B在 $y = \frac{k}{x}$ ，则k =.

查看试题解析
14. 如图，▱ABCD中，E是AB延长线上一点，DE交直线BC于点F，若BE∶AB＝2∶3，△BEF的面积为4，则△ADF的面积为.

查看试题解析
15. 如图，△ABC中，AC=BC=4，∠ACB=90°，D为边AB上一动点（不与A、B重合），⊙D与BC切于E点，E点关于CD的对称点F在△ABC的一边上，则BD=.

查看试题解析
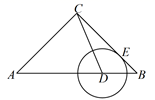16. 在平面直角坐标系xOy中，抛物线y = x² – 2 m x – 2m – 2与直线y =-x-2 交于C，D两点，将抛物线在C、D两点之间的部分(不含C、D）上恰有两个点的横坐标为整数，则m的取值范围为.

查看试题解析

三、解答题

17.

(1)、计算： ${(- 1)}^{2019} - \sqrt[3]{27} + {(π - 3.14)}^{0} + \tan 60 °$

(2)、解方程： $\frac{x - 3}{x} = \frac{x}{x + 1}$

查看试题解析
18. 某校用随机抽样的方法在九年级开展了“你是否喜欢网课”的调查，并将得到的数据整理成了以下统计图（不完整）.

(1)、此次共调查了名学生；

(2)、请将条形统计图补充完整；

(3)、若该学校九年级共有300名学生，请你估计其中“非常喜欢”网课的人数.

查看试题解析
19. 在一个不透明的口袋中有标号为1，2，3，4的四个小球，除数字不同外，小球没有任何区别，摸球前先搅拌均匀，每次摸一个球

(1)、摸出一个球，摸到标号为偶数的概率为．

(2)、从袋中不放回地摸两次，用列表或树状图求出两球标号数字为一奇一偶的概率．

查看试题解析
20. 如图，在△ABC中，AB=AC，D是BC延长线上一点，E是AD的一点，EC⊥BD.

(1)、若E是AD的中点，求证：BC＝2CD；

(2)、连接BE交AC与F，若BC=CD，AB＝2，求CF的长.

查看试题解析
21. 甲、乙两家某商品专卖店一月份销售额分别为10万元和15万元，三月份销售额甲店比乙店多10万元.已知甲店二、三月份销售额的月平均增长率是乙店二、三月份月平均增长率的2倍，求甲店、乙店这两个月的月平均增长率各是多少？

查看试题解析
22. 如图，∠ACB=90°，AC=BC，AB为水平边，D为AB边上一点.

(1)、只用圆规在B的正上方作一点E，使BE=AD；

(2)、在（1）的条件下，连接DE，若AC= $4 \sqrt{2}$ ，AD=3，求DE的长度.

查看试题解析
23.
某海域有A、B、C三艘船正在捕鱼作业，C船突然出现故障，向A、B两船发出紧急求救信号，此时B船位于A船的北偏西72°方向，距A船24海里的海域，C船位于A船的北偏东33°方向，同时又位于B船的北偏东78°方向．

(1)、求∠ABC的度数；

(2)、A船以每小时30海里的速度前去救援，问多长时间能到出事地点．（结果精确到0.01小时）．
（参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）

查看试题解析
24. 如图，在平面系中，一次函数 $y = a x - a + 6$ 的图像经过定点A，反比例函数 $y = \frac{k}{x}$ 的图像经过点A，且与一次函数 $y = a x - a + 6$ 的图像相交于点B（ $- 3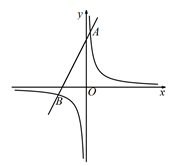$ ，m）.

(1)、求m、a的值；

(2)、设横坐标为n的点P在反比例函数图象的第三象限上，且在点B右侧，连接AP、BP，△ABP的面积为12，求代数式 $n^{2} - n$ 的值.

查看试题解析
25. 如图，AB＝4，C为射线BA上一动点，以BC为边向上作正三角形BCD，⊙O过A、C、D三点，E为⊙O上一点，满足AD＝ED，直线CE交直线AD于F.

(1)、求证：CE∥BD；

(2)、设CF=a，若C在线段AB上运动.
①求点E运动的路径长；

②求a的范围；

(3)、若AC＝1，求 tan∠DEC.

查看试题解析
26. 在平面直角坐标系xOy中，抛物线G： $y_{1} = a x^{2} - 2 a x - 3 a (a < 0)$ 与x轴交于A、B两点（点A在点B的左侧），与y轴交于C点；一次函数 $y_{2} = m x + n$ （ $m < 0$ ）的图像为直线 $l$ .

(1)、求A、B两点的坐标；

(2)、当1≤x≤2时， $- m$ ≤ $y_{1}$ ≤ $- n$ ，试说明：抛物线G的顶点不在直线 $l$ 上；

(3)、设 $a = - 3$ ，直线 $l$ 与线段AC交于D点，与y轴交于E点，与抛物线G的对称轴交于F 点，当A、C两点到直线 $l$ 距离相等时，是否存在整数n，使F点在直线BE的上方?若存在，求n的值；若不存在，请说明理由.

查看试题解析