河南省信阳市潢川县2020年数学中考一模试卷
试卷更新日期:2020-08-18 类型:中考模拟
一、选择题
-
1. 下列实数中的无理数是( )A、π B、 C、-0.7 D、2. 郑州已经正式被定为国家中心城市!作为郑州发展的核心,郑州机场2016年全年完成旅客吞吐量2076万次,同比增长20%,强数据2076万用科学记数法表示为( )A、2.076×108 B、2076×106 C、0.2076×108 D、2.076×1073. 下列四个几何体中,左视图为圆的是( )A、
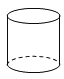 B、
B、 C、
C、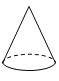 D、
D、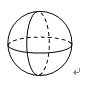 4. 已知a≠0,下列计算正确的是( )A、a2+a3=a5 B、a2•a3=a6 C、a3÷a2=a D、(a2)3=a55. 已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2的度数是( )
4. 已知a≠0,下列计算正确的是( )A、a2+a3=a5 B、a2•a3=a6 C、a3÷a2=a D、(a2)3=a55. 已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2的度数是( )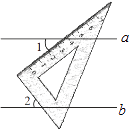 A、37° B、53° C、63° D、27°6. 上体育课时,小明5次投掷实心球的成绩如下表所示,则这组数据的众数与中位数分别是( )
A、37° B、53° C、63° D、27°6. 上体育课时,小明5次投掷实心球的成绩如下表所示,则这组数据的众数与中位数分别是( )1
2
3
4
5
成绩(m)
8.2
8.0
8.2
7.5
7.8
A、8.2,8.2 B、8.0,8.2 C、8.2,7.8 D、8.2,8.07. 如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是( )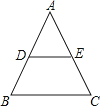 A、AD=AE B、DB=EC C、∠ADE=∠C D、DE=BC8. 如图,在平面直角坐标系系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y= 在第一象限内的图象交于点B,连接BO.若S△OBC=1,tan∠BOC= ,则k2的值是( )
A、AD=AE B、DB=EC C、∠ADE=∠C D、DE=BC8. 如图,在平面直角坐标系系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y= 在第一象限内的图象交于点B,连接BO.若S△OBC=1,tan∠BOC= ,则k2的值是( ) A、﹣3 B、1 C、2 D、39. 如图,在▱ABCD中,AB=6,BC=8,∠BCD的平分线交AD于点E,交BA的延长线于点F,则AE+AF的值等于( )
A、﹣3 B、1 C、2 D、39. 如图,在▱ABCD中,AB=6,BC=8,∠BCD的平分线交AD于点E,交BA的延长线于点F,则AE+AF的值等于( ) A、2 B、3 C、4 D、610. 如图,一根长为5米的竹竿AB斜立于墙MN的右侧,底端B与墙角N的距离为3米,当竹竿A下滑x米时,底端B便随着向右滑行y米,反映y与x变化关系的大致图象是( )
A、2 B、3 C、4 D、610. 如图,一根长为5米的竹竿AB斜立于墙MN的右侧,底端B与墙角N的距离为3米,当竹竿A下滑x米时,底端B便随着向右滑行y米,反映y与x变化关系的大致图象是( ) A、
A、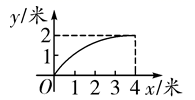 B、
B、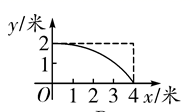 C、
C、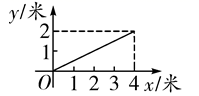 D、
D、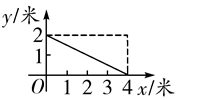
二、填空题
-
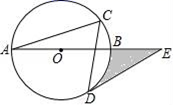
11. 计算 =.12. 已知关于x的方程3a﹣x=+3的解为2,则代数式a2﹣2a+1的值是13. 把三张形状、大小相同但画面不同的风景图片,都按同样的方式剪成相同的两片,然后堆放到一起混合洗匀,从这堆图片中随机抽出两张,这两张图片恰好能组成一张原风景图片的概率是 .14. 如图,⊙O的半径是4,圆周角∠C=60°,点E时直径AB延长线上一点,且∠DEB=30°,则图中阴影部分的面积为.
 15. 如图,△ABC中,AB= ,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为.
15. 如图,△ABC中,AB= ,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为.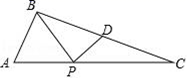
三、解答题
-
16. 先化简,再求值:( ﹣a)÷(1+ ),其中a是不等式﹣ <a< 的整数解.17. 小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图。请根据图中信息,解答下列问题:
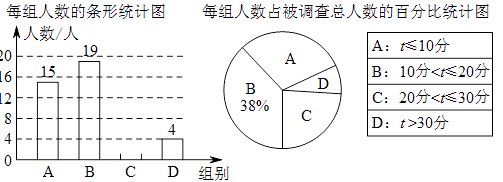 (1)、这次被调查的总人数是多少?(2)、试求表示A组的扇形圆心角的度数,并补全条形统计图;(3)、如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比。18. 如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.
(1)、这次被调查的总人数是多少?(2)、试求表示A组的扇形圆心角的度数,并补全条形统计图;(3)、如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比。18. 如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.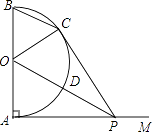 (1)、求证:△OAP≌△OCP;(2)、若半圆O的半径等于2,填空:
(1)、求证:△OAP≌△OCP;(2)、若半圆O的半径等于2,填空:①当AP=时,四边形OAPC是正方形;
②当AP=时,四边形BODC是菱形.
19.数学小组的两位同学准备测量两幢教学楼之间的距离,如图,两幢教学楼AB和CD之间有一景观池(AB⊥BD,CD⊥BD),一同学在A点测得池中喷泉处E点的俯角为42°,另一同学在C点测得E点的俯角为45°(点B,E,D在同一直线上),两个同学已经在学校资料室查出楼高AB=15m,CD=20m,求两幢教学楼之间的距离BD.
(结果精确到0.1m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
 20. 如图,函数 与 的图像在第一象限内交于点A,在求点A坐标时,小明由于看错了k,解得A(1 , 3);小华由于看错了m,解得A(1, ).
20. 如图,函数 与 的图像在第一象限内交于点A,在求点A坐标时,小明由于看错了k,解得A(1 , 3);小华由于看错了m,解得A(1, ). (1)、求这两个函数的关系式及点A的坐标;(2)、根据函数图象回答:若 ,请直接写出x的取值范围.21. “六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
(1)、求这两个函数的关系式及点A的坐标;(2)、根据函数图象回答:若 ,请直接写出x的取值范围.21. “六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表: (1)、小张如何进货,使进货款恰好为1300元?(2)、要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.22.(1)、已知:等边△ABC的边长为4,点P在线段AB上,点D在线段AC上,且△PDE为等边三角形,当点P与点B重合时(如图1),AD+AE的值为;
(1)、小张如何进货,使进货款恰好为1300元?(2)、要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.22.(1)、已知:等边△ABC的边长为4,点P在线段AB上,点D在线段AC上,且△PDE为等边三角形,当点P与点B重合时(如图1),AD+AE的值为;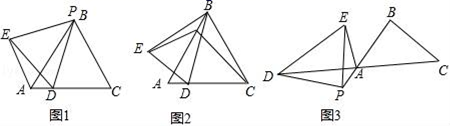 (2)、[类比探究]
(2)、[类比探究]在上面的问题中,如果把点P沿BA方向移动,使PB=1,其余条件不变(如图2),AD+AE的值是多少?请写出你的计算过程;
(3)、[拓展迁移]如图3,△ABC中,AB=BC,∠ABC=a,点P在线段BA延长线上,点D在线段CA延长线上,在△PDE中,PD=PE,∠DPE=a,设AP=m,则线段AD、AE有怎样的等量关系?请用含m,a的式子直接写出你的结论.
23. 如图,抛物线 与直线AB交于点A(-1,0),B(4, ).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.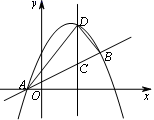 (1)、求抛物线的解析式;(2)、设点D的横坐标为m,则用m的代数式表示线段DC的长;(3)、在(2)的条件下,若△ADB的面积为S,求S关于m的函数关系式,并求出当S取最大值时的点C的坐标;(4)、当点D为抛物线的顶点时,若点P是抛物线上的动点,点Q是直线AB上的动点,判断有几个位置能使以点P,Q,C,D为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
(1)、求抛物线的解析式;(2)、设点D的横坐标为m,则用m的代数式表示线段DC的长;(3)、在(2)的条件下,若△ADB的面积为S,求S关于m的函数关系式,并求出当S取最大值时的点C的坐标;(4)、当点D为抛物线的顶点时,若点P是抛物线上的动点,点Q是直线AB上的动点,判断有几个位置能使以点P,Q,C,D为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.