广西玉林市玉州区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-18 类型:期末考试
一、选择题:本大题共12小题,每小题3分,共36分。
-
1. 下列四个点中,在函数 的图象上的是( )A、 B、 C、 D、2. 在平行四边形ABCD中,已知 , ,则它的周长为( )A、8 B、10 C、14 D、163. 如果某函数的图象如图所示,那么y随x的增大而( )
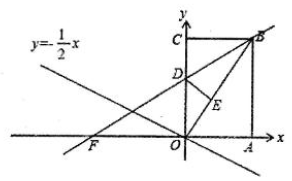
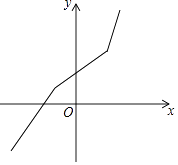 A、增大 B、减小 C、不变 D、有时增大有时减小4. 下列运算错误的是( )A、 B、 C、 D、5. 对于 的理解错误的是( )A、是实数 B、是最简二次根式 C、 D、能与 进行合并6. 如图,在平面直角坐标系中,点 在第一象限,若点A关于x轴的对称点B在直线 上,则m的值为( )
A、增大 B、减小 C、不变 D、有时增大有时减小4. 下列运算错误的是( )A、 B、 C、 D、5. 对于 的理解错误的是( )A、是实数 B、是最简二次根式 C、 D、能与 进行合并6. 如图,在平面直角坐标系中,点 在第一象限,若点A关于x轴的对称点B在直线 上,则m的值为( )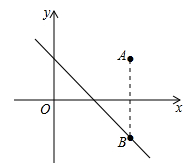 A、-1 B、1 C、2 D、37. 如图,描述了小勤同学某日的一段生活过程:他早上从家里跑步去书店,在书店买了一本书后,马上就去早餐店吃早餐,吃完早餐后,立即散步走回家.图象中的平面直角坐标系中的x表示时间,y表示小勤离家的距离.请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )
A、-1 B、1 C、2 D、37. 如图,描述了小勤同学某日的一段生活过程:他早上从家里跑步去书店,在书店买了一本书后,马上就去早餐店吃早餐,吃完早餐后,立即散步走回家.图象中的平面直角坐标系中的x表示时间,y表示小勤离家的距离.请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )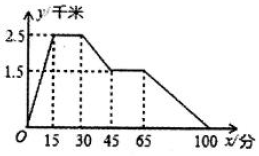 A、小勤从家到新华书店的平均速度是10千米/分钟 B、小勤买书花了15分钟 C、小勤吃早餐花了20分钟 D、从早餐店到小勤家的距离是1.5千米8. 如图,一次函数 与一次函数 的图象交于点 ,则关于x的不等式 的解集是( )
A、小勤从家到新华书店的平均速度是10千米/分钟 B、小勤买书花了15分钟 C、小勤吃早餐花了20分钟 D、从早餐店到小勤家的距离是1.5千米8. 如图,一次函数 与一次函数 的图象交于点 ,则关于x的不等式 的解集是( )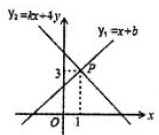 A、 B、 C、 D、9. 如图在正方形网格中,每个小正方形的边长均为1,则在 中(点A,B,C都在格点上),边长为无理数的边有( )
A、 B、 C、 D、9. 如图在正方形网格中,每个小正方形的边长均为1,则在 中(点A,B,C都在格点上),边长为无理数的边有( )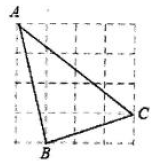 A、3条 B、2条 C、1条 D、0条10. 某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差 .后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )A、平均分不变,方差变大 B、平均分不变,方差变小 C、平均分和方差都不变 D、平均分和方差都改变11. 如图,正方形ABCD的面积为8,菱形AECF的面积为4,则EF的长是( )
A、3条 B、2条 C、1条 D、0条10. 某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差 .后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )A、平均分不变,方差变大 B、平均分不变,方差变小 C、平均分和方差都不变 D、平均分和方差都改变11. 如图,正方形ABCD的面积为8,菱形AECF的面积为4,则EF的长是( )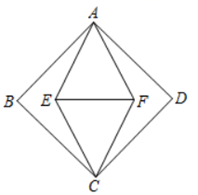 A、4 B、 C、2 D、112. 已知菱形 在平面直角坐标系的位置如图所示,顶点 , ,点P是对角线 上的一个动点 ,当 最短时,点P的坐标为( )
A、4 B、 C、2 D、112. 已知菱形 在平面直角坐标系的位置如图所示,顶点 , ,点P是对角线 上的一个动点 ,当 最短时,点P的坐标为( )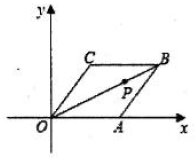 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本大题共6小题,每小题3分,共18分,
-
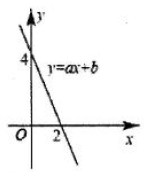
13. 计算: .14. 将直线 向上平移 个单位后得到的解析式为 .15. 小明用 计算一组数据的方差,那么 .16. 如图所示,一次函数 的图象与x轴交于点 ,与y轴相交于点 ,结合图象可知,关于x的方程 的解是 .
 17. 如图,在 的正方形网格中,每个小正方形边长为1,点A,B,C均为格点,以点A为圆心, 长为半径作弧,交格线于点D,则 的长为 .
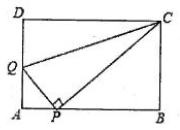
17. 如图,在 的正方形网格中,每个小正方形边长为1,点A,B,C均为格点,以点A为圆心, 长为半径作弧,交格线于点D,则 的长为 .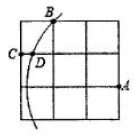 18. 如图,长方形纸片 中, , .点E是 边上一点,连接 并将 沿 折叠,得到 ,以C,E, 为顶点的三角形是直角三角形时, 的长为 .
18. 如图,长方形纸片 中, , .点E是 边上一点,连接 并将 沿 折叠,得到 ,以C,E, 为顶点的三角形是直角三角形时, 的长为 .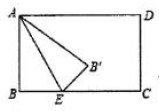
三、解答题:本大题共8小题,满分共66分。
-
19. 计算:(1)、 ;(2)、 .20. 已知一次函数 的图象经过点 .(1)、求该函数解析式,并在平面直角坐标系中画出该函数的图象;(2)、若点 在该函数图象的下方,求n的取值范围.21. 如图,某斜拉桥的主梁 垂直于桥面 于点D,主梁上两根拉索 、 长分别为13米、20米.
 (1)、若拉索 ,求固定点B、C之间的距离;(2)、若固定点B、C之间的距离为21米,求主梁 的高度.22. 上周六上午7点,小颖同爸爸妈妈一起从玉林出发去南宁看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离y(千米)与他们路途所用的时间x(时)之间的函数图象,请根据以上信息,解答下列问题:
(1)、若拉索 ,求固定点B、C之间的距离;(2)、若固定点B、C之间的距离为21米,求主梁 的高度.22. 上周六上午7点,小颖同爸爸妈妈一起从玉林出发去南宁看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离y(千米)与他们路途所用的时间x(时)之间的函数图象,请根据以上信息,解答下列问题: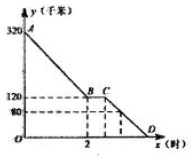 (1)、求直线 所对应的函数关系式;(2)、已知小颖一家出服务区后,行驶30分钟时,距姥姥家还有80千米,问小颖一家当天几点到达姥姥家?23. 为了推动我区教育教学发展,加快教师的成长,在某次研讨课活动中,为了分析某节复习课的教学效果,课前,陈老师让1801班每位同学做6道类似题目(与这节课内容相关),解题情况如图所示:课后,再让学生做6道类似的题目.结果如表所示.已知每位学生至少答对1题.
(1)、求直线 所对应的函数关系式;(2)、已知小颖一家出服务区后,行驶30分钟时,距姥姥家还有80千米,问小颖一家当天几点到达姥姥家?23. 为了推动我区教育教学发展,加快教师的成长,在某次研讨课活动中,为了分析某节复习课的教学效果,课前,陈老师让1801班每位同学做6道类似题目(与这节课内容相关),解题情况如图所示:课后,再让学生做6道类似的题目.结果如表所示.已知每位学生至少答对1题.
课后解题情况统计表
答对题数
频数(人)
1
2
2
3
3
3
4
a
5
9
6
13
合计
b
(1)、根据图表信息填空:a=;b= .(2)、该班课前解题时答对题数的众数是;课后答对题数的中位数是 .(3)、请选择适当的统计量,从两个不同的角度评价这节复习课的教学效果.24. 随着新冠病毒在全世界蔓延,疫情期间口罩成为紧缺物资,某市防控部门要求市民佩戴口罩出行,某药店购进甲种可有效预防新冠病毒的 型口罩和乙种普通口罩共400个,这两种口罩的进价和售价如表所示:甲
乙
进价(元/个)
18
6
售价(元/个)
22
9
该药店计划购进乙种普通口罩x个,两种口罩全部销售完后可获利润y元.
(1)、求出利润y与x的函数关系式;(2)、已知购进甲种口罩的数量不多于乙种口罩数量的3倍,利用函数性质,说明该药店怎样进货,使全部销售获得的利润最大?并求出最大利润.