浙江省仙居县2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2020-08-18 类型:期末考试
一、选择题:本大题共10个小题,每小题3分,共30分.
-
1. 下面四个图形中, 与 是对顶角的是( )A、
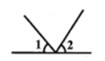 B、
B、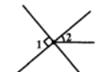 C、
C、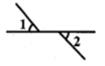 D、
D、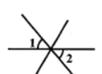 2. 下列方程组中是二元一次方程组的是( )A、 B、 C、 D、3. 下列问题最适合用抽样调查的是( ).A、调查春节联欢晚会的收视率. B、长征5B火箭发射前各零部件的检查. C、了解某班学生的身高情况 D、某企业招聘,对应试人员进行面试.4. 把方程 改写成用含x的式子表示y的形式,正确的是( )A、 B、 C、 D、5. 如图,不等式组 的解集在数轴上表示正确的是( )A、
2. 下列方程组中是二元一次方程组的是( )A、 B、 C、 D、3. 下列问题最适合用抽样调查的是( ).A、调查春节联欢晚会的收视率. B、长征5B火箭发射前各零部件的检查. C、了解某班学生的身高情况 D、某企业招聘,对应试人员进行面试.4. 把方程 改写成用含x的式子表示y的形式,正确的是( )A、 B、 C、 D、5. 如图,不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、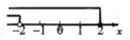 D、
D、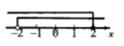 6. 下列命题中是真命题的是( )A、 B、若 ,则 C、垂线最短 D、同旁内角相等,两直线平行7. 如果点 在平面直角坐标系的 轴上,则m=( )A、-3 B、-2 C、-1 D、08. 篮球比赛中,每场比赛都要分出胜负,每队胜1场得3分,负一场扣1分,某队在8场比赛中得到12分,若设该队胜的场数为 ,负的场数为 ,则可列出方程组( )A、 B、 C、 D、9. 若 , ,且 ,则 的值为( )A、-9 B、-2 C、±9 D、110. 现有 四个正整数,将它们随机抽取两个并相加,所得的和都是 中的一个,并且 这4个数都能取到,那么 这四个正整数( )A、各不相等 B、有且只有两个数相等 C、有且只有三个数相等 D、全部相等
6. 下列命题中是真命题的是( )A、 B、若 ,则 C、垂线最短 D、同旁内角相等,两直线平行7. 如果点 在平面直角坐标系的 轴上,则m=( )A、-3 B、-2 C、-1 D、08. 篮球比赛中,每场比赛都要分出胜负,每队胜1场得3分,负一场扣1分,某队在8场比赛中得到12分,若设该队胜的场数为 ,负的场数为 ,则可列出方程组( )A、 B、 C、 D、9. 若 , ,且 ,则 的值为( )A、-9 B、-2 C、±9 D、110. 现有 四个正整数,将它们随机抽取两个并相加,所得的和都是 中的一个,并且 这4个数都能取到,那么 这四个正整数( )A、各不相等 B、有且只有两个数相等 C、有且只有三个数相等 D、全部相等二、填空题(本大题共6个小题,每小题3分,共18分)
-
11. 请用不等式表示“ 的2倍与3的和大于1”:.12. 请写出一个比2大且比4小的无理数:.13. 关于 的不等式 的最大正整数解是.14. 给出下列10个数据:63,62,67,69,66,64,65,68,64,65,对这些数据编制频数分布表,其中 这组的频数是.15. 在平面直角坐标系中, ,且 轴,若点A的坐标为 ,则点B的坐标为.16. 为防控新冠疫情,做好个人防护,小君去药店购买口罩,若买6个平面口罩和4个 口罩,则她所带的钱还剩下10元;若买4个平面口罩和6个 口罩,则她所带的钱还缺8元,若只买10个 口罩,则她所带的钱还缺元.
三、解答题:本大题共8题,第17题5分,第18题6分,第19题7分,第20-22题每题6分,第23-24题每题8分,满分52分.
-
17. 计算:18. 解方程组:19. 解不等式 ,并写出每一步的依据.20. 三角形ABC在平面直角坐标系中的位置如图所示(图中每个小方格边长均为1个单位长度).将三角形ABC先向左平移4个单位长度,再向下平移3个单位长度得到三角形 .
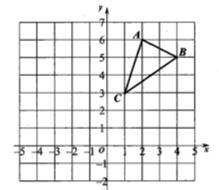 (1)、在图中画出三角形 ;(2)、求三角形ABC的面积.21. 某校七年级举行“数学计算能力“比赛,比赛结束后,随机抽查部分学生的成绩,根据抽查结果绘制成如下的统计图表.
(1)、在图中画出三角形 ;(2)、求三角形ABC的面积.21. 某校七年级举行“数学计算能力“比赛,比赛结束后,随机抽查部分学生的成绩,根据抽查结果绘制成如下的统计图表.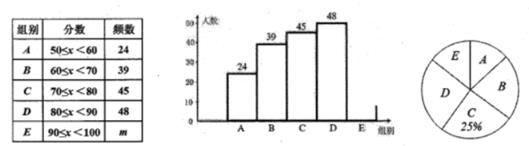
根据以上信息解答下列问题:
(1)、共抽查了名学生,统计图表中,m=:(2)、请补全直方图;(3)、若七年级共有800名学生,分数不低于80分为优良,请你估算本次比赛七年级分数优良的学生的人数.22. 如图,已知: , , .求证: .
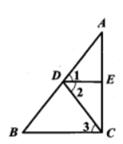
证明:∵ , (已知)
∴ (▲ )
∴ (▲ )
∴ ▲ (▲ )
▲ (▲ )
又∵ (已知)
∴ (等量代换)
23. 综合与实践:七年级下册第五章我们学习了平行线的性质与判定,今天我们继续探究:折纸中的数学—长方形纸条的折叠与平行线.
 (1)、知识初探
(1)、知识初探如图1,长方形纸条ABCD中, , , ,将长方形纸条沿直线EF折叠,点A落在 处,点D落在 处, 交CD于点G.
①若 ,求 的度数;
②若 ,则 ▲ (用含 的式子表示)
(2)、类比再探如图2,在图1的基础上将 对折,点C落在直线 上的 处,点B落在 处,得到折痕 ,则折痕EF与GH有怎样的位置关系?并说明理由.
24. 目前全球都在针对新冠疫情作积极防控,大型公共场所经常用到消毒产品消毒.某工厂计划生产A、B两种消毒产品共80箱,需购买甲、乙两种材料.已知生产一箱A产品需甲种材料3千克,乙种材料1千克;生产一箱B产品需甲、乙两种材料各2千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料3千克和乙种材料2千克共需资金140元.(1)、甲、乙两种材料的单价分别为每千克多少元?(2)、现工厂用于购买甲、乙两种材料的资金不超过8800元,且生产B产品不少于38箱,问符合生产条件的生产方案有哪几种?(3)、在(2)的条件下,若生产一箱A产品需加工费40元,若生产一箱B产品需加工费50元,应选择哪种生产方案,使生产这80箱产品的成本最低?(成本=材料费+加工费)