辽宁省大连市名校联盟2019-2020学年八年级上学期数学10月月考试卷
试卷更新日期：2020-08-17 类型：月考试卷
一、单选题。
-
1. 以下列各组线段为边，能组成三角形的是( )A、2cm，3cm，5cm B、3cm，3cm，6cm C、5cm，8cm，2cm D、4cm，5cm，6cm2. 一个三角形三个内角的度数之比为4：5：6，这个三角形一定是（ ）A、直角三角形 B、等腰三角形 C、锐角三角形 D、钝角三角形3. 如图，已知矩形 一条直线将该矩形 分割成两个多边形（含三角形），若这两个多边形的内角和分别为 和 则 不可能是（ ）.
A、 B、 C、 D、4. 如图，已知 ，则不一定能使 的条件是（ ）
A、 B、 C、 D、5. 已知等腰三角形的两边长是4和9，则等腰三角形的周长为（ ）A、17 B、17或22 C、22 D、166. 如图，在锐角△ABC中，CD，BE分别是AB，AC边上的高，CD，BE交于点P，∠A=50°，则∠PBC的度数是（ ）
A、150° B、130° C、120° D、100°7. 如图，高速公路上有A，B两点相距25km，C、D为两村庄，已知DA＝10km，CB＝15km.DA⊥AB于A，CB⊥AB于B，现要在AB上建一个服务站E，使得C、D两村庄到E站的距离相等，则AE的长是（ ）km.
A、5 B、10 C、15 D、258. 如图，在△ABC中，AB＝4，AC＝6，∠ABC和∠ACB的平分线交于O点，过点O作BC的平行线交AB于M点，交AC于N点，则△AMN的周长为（ ）
A、7 B、8 C、9 D、109. 如图，在△ABC中，AC=5，中线AD=7，则AB边的取值范围是（ ）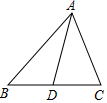
A、 B、 C、 D、10. 如图△ABC中，∠B＝∠C ， BD＝CF ， BE＝CD ， ∠EDF＝α ， 则下列结论正确的是（ ）
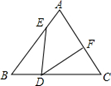A、α＋2∠A＝180° B、2α＋∠A＝180° C、α＋∠A＝90° D、α＋∠A＝180°二、填空题。
-
11. 一个n边形的每个内角都等于140°，则n＝.12. 在Rt△ABC中，∠C＝90°，∠A＝30°，AB＝6，则AC＝ ．13. 如图，已知△ABC中，∠C＝90°，AC＝BC，AB＝8m，BD平分∠ABC交AC于点D，过D作DE⊥AB于点E，则△ADE的周长为cm.
14. 如图，所示，在△ABC中，D在AC上，连结BD，且∠ABC=∠C=∠1，∠A=∠3，则∠A 的度数为.
15. 已知点A(0，1)，B(3，1)，C(4，3).如果在y轴的左侧存在一点D，使得△ABD与△ABC全等，那么点D的坐标为.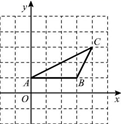
16. 如图，四边形ABCD中，AC＝BC＝BD，且AC⊥BD，若AB＝a，则△ABD的面积为.（用含a的式子表示）
三、解答题。
-
17. △ABC中，∠B＝∠C+10°，∠A＝∠B+10°，求△ABC的各内角的度数.18. 计算：如图，点B、F、C、E在一条直线上，FB=CE，AB∥ED，AC∥FD.求证：AC=DF.
19. 已知△ABC的面积为20cm2 ， AD为BC边上的高，且AD＝8cm，CD＝2cm，求BD的长度.20. 如图所示，在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）.
（ 1 ）求出△ABC的面积；
（ 2 ）在图形中作出△ABC关于x轴的对称图形△A1B1C1 ， 写出点A1 ， B1 ， C1的坐标；
（ 3 ）点P在y轴上，使PB+PC的长最小，请在y轴上标出点P的位置.
21. 已知：如图E在△ABC的边AC上，且∠AEB=∠ABC.
(1)、求证：∠ABE=∠C；(2)、若∠BAE的平分线AF交BE于F，FD∥BC交AC于D，设AB=5，AC=8，求DC的长.22. 如图，∠AOB=30°，点P是∠AOB内一点，PO=8，在∠AOB的两边分别有点R、Q（均不同于O），求△PQR周长的最小值．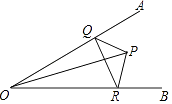
23. 如图(1)，Rt△ABC中，∠ACB=-90°，CD⊥AB，垂足为D.AF平分∠CAB，交CD于点E，交CB于点F
(1)、求证：CE=CF.(2)、将图（1）中的△ADE沿AB向右平移到△A’D’E’的位置，使点E’落在BC边上，其它条件不变，如图（2）所示.试猜想：BE'与CF有怎样的数量关系?请证明你的结论.24. 如图，在△ABC中，AB=AC，AH⊥BC，垂足为H，D为直线BC上一动点(不与点BC重合)，在AD的右侧作△ADE，使得AE=AD，∠DAE=∠BAC，连接CE.
(1)、当D在线段BC上时，求证：△BAD≌△CAE；(2)、当点D运动到何处时，AC⊥DE，并说明理由；(3)、当CE∥AB时，若△ABD中最小角为20°，试探究∠ADB的度数(直接写出结果，无需写出求解过程).25. 阅读下面材料，完成（1）-（3）题数学课上，老师出示了这样一道题：如图，△ABD和△ACE中，AB＝AD，AC＝AE，∠DAB＝∠CAE＝α，连接DC、BE交于点F，过A作AG⊥DC于点G，探究线段FG、FE、FC之间的数量关系，并证明.
同学们经过思考后，交流了自 己的想法：
小明：“通过观察和度量，发现线段BE与线段DC相等.”
小伟：“通过观察发现，∠AFE与α存在某种数量关系.”
老师：“通过构造全等三角形，从而可以探究出线段FG、FE、FC之间的数量关系.”
(1)、求证：BE＝CD；(2)、求∠AFE的度数（用含α的式子表示）；(3)、探究线段FG、FE、FC之间的数量关系，并证明.26. 如图，点A、B分别在x轴的负半轴和y轴的正半轴上，点C（2，﹣2），CA、CB分别交坐标轴于D、E，CA⊥AB，且CA＝AB
(1)、求点B的坐标；(2)、如图2，连接DE，求证：BD﹣AE＝DE；(3)、如图3，若点F为（4，0），点P在第一象限内，连接PF，过P作PM⊥PF交y轴于点M，在PM上截取PN＝PF，连接PO、BN，过P作∠OPG＝45°交BN于点G，求证：点G是BN的中点.