四川省雅安市2020年中考数学试卷
试卷更新日期:2020-08-17 类型:中考真卷
一、单选题
-
1. 2020的相反数是( )A、 2020 B、﹣2020 C、 D、2. 不等式组 的解集在数轴上表示正确的是( )A、
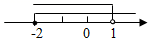 B、
B、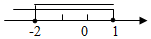 C、
C、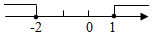 D、
D、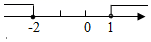 3. 一个几何体由若干大小相同的小正方体组成,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少为( )
3. 一个几何体由若干大小相同的小正方体组成,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少为( )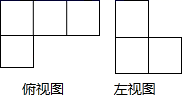 A、4 B、5 C、6 D、74. 下列式子运算正确的是( )A、 B、 C、 D、5. 下列四个选项中不是命题的是( )A、对顶角相等 B、过直线外一点作直线的平行线 C、三角形任意两边之和大于第三边 D、如果 ,那么6. 已知 ,则a+2b的值是( )A、4 B、6 C、8 D、107. 若分式 的值为0,则x的值为( )A、0 B、1 C、﹣1 D、±18. 在课外活动中,有10名同学进行了投篮比赛,限每人投10次,投中次数与人数如下表:
A、4 B、5 C、6 D、74. 下列式子运算正确的是( )A、 B、 C、 D、5. 下列四个选项中不是命题的是( )A、对顶角相等 B、过直线外一点作直线的平行线 C、三角形任意两边之和大于第三边 D、如果 ,那么6. 已知 ,则a+2b的值是( )A、4 B、6 C、8 D、107. 若分式 的值为0,则x的值为( )A、0 B、1 C、﹣1 D、±18. 在课外活动中,有10名同学进行了投篮比赛,限每人投10次,投中次数与人数如下表:投中次数
5
7
8
9
10
人数
2
3
3
1
1
则这10人投中次数的平均数和中位数分别是( )
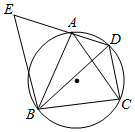
A、 B、 C、 D、9. 如图,在 中, ,若 ,则 的长为( )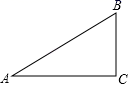 A、8 B、12 C、 D、10. 如果关于x的一元二次方程 有两个实数根,那么 的取值范围是( )A、 B、 且 C、 且 D、11. 如图, 内接于圆, ,过点C的切线交 的延长线于点 .则 ( )
A、8 B、12 C、 D、10. 如果关于x的一元二次方程 有两个实数根,那么 的取值范围是( )A、 B、 且 C、 且 D、11. 如图, 内接于圆, ,过点C的切线交 的延长线于点 .则 ( )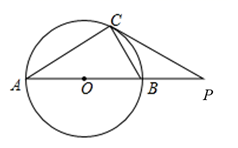 A、 B、 C、 D、12. 已知,等边三角形 和正方形 的边长相等,按如图所示的位置摆放(C点与E点重合),点 共线, 沿 方向匀速运动,直到B点与F点重合.设运动时间为 ,运动过程中两图形重叠部分的面积为 ,则下面能大致反映 与 之间关系的函数图象是( )
A、 B、 C、 D、12. 已知,等边三角形 和正方形 的边长相等,按如图所示的位置摆放(C点与E点重合),点 共线, 沿 方向匀速运动,直到B点与F点重合.设运动时间为 ,运动过程中两图形重叠部分的面积为 ,则下面能大致反映 与 之间关系的函数图象是( )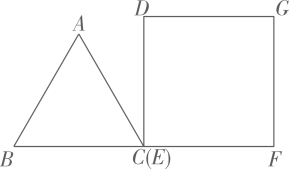 A、
A、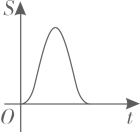 B、
B、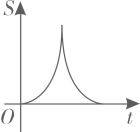 C、
C、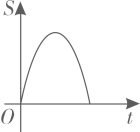 D、
D、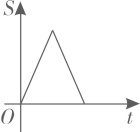
二、填空题
-
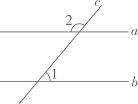
13. 如图, 与 都相交, ,则 .
 14. 如果用 表示温度升高3摄氏度,那么温度降低2摄氏度可表示为 .15. 从 中任取一数作为 ,使抛物线 的开口向上的概率为 .16. 若 ,则 .17. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形 ,对角线 交于点O.若 ,则 .
14. 如果用 表示温度升高3摄氏度,那么温度降低2摄氏度可表示为 .15. 从 中任取一数作为 ,使抛物线 的开口向上的概率为 .16. 若 ,则 .17. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形 ,对角线 交于点O.若 ,则 .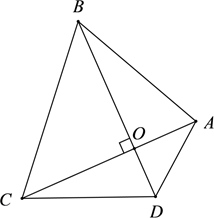
三、解答题
-
18.(1)、计算: ;(2)、先化简 ,再从 中选择合适的 值代入求值.19. 从某校初三年级中随机抽查若干名学生摸底检测的数学成绩(满分为120分),制成如图的统计直方图,已知成绩在80~90分(含80分,不含90分)的学生为抽查人数的 ,且规定成绩大于或等于100分为优秀.
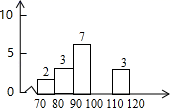 (1)、求被抽查学生人数及成绩在100~110分的学生人数 ;(2)、在被抽查的学生中任意抽取1名学生,则这名学生成绩为优秀的概率;(3)、若该校初三年级共有300名学生,请你估计本次检测中该校初三年级数学成绩为优秀的人数.20. 某班级为践行“绿水青山就是金山银山”的理念,开展植树活动.如果每人种3棵,则剩86棵;如果每人种5棵,则最后一人有树种但不足3棵.请问该班有多少学生?本次一共种植多少棵树?(请用一元一次不等式组解答)21. 如图,已知边长为10的正方形 是 边上一动点(与 不重合),连结 是 延长线上的点,过点E作 的垂线交 的角平分线于点F,若 .
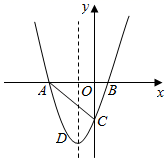
(1)、求被抽查学生人数及成绩在100~110分的学生人数 ;(2)、在被抽查的学生中任意抽取1名学生,则这名学生成绩为优秀的概率;(3)、若该校初三年级共有300名学生,请你估计本次检测中该校初三年级数学成绩为优秀的人数.20. 某班级为践行“绿水青山就是金山银山”的理念,开展植树活动.如果每人种3棵,则剩86棵;如果每人种5棵,则最后一人有树种但不足3棵.请问该班有多少学生?本次一共种植多少棵树?(请用一元一次不等式组解答)21. 如图,已知边长为10的正方形 是 边上一动点(与 不重合),连结 是 延长线上的点,过点E作 的垂线交 的角平分线于点F,若 . (1)、求证: ;(2)、若 ,求 的面积;(3)、请直接写出 为何值时, 的面积最大.22. 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)、求证: ;(2)、若 ,求 的面积;(3)、请直接写出 为何值时, 的面积最大.22. 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.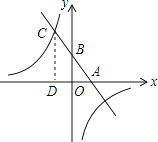 (1)、求一次函数与反比例函数的解析式;(2)、求两函数图象的另一个交点坐标;(3)、直接写出不等式;kx+b≤ 的解集.
(1)、求一次函数与反比例函数的解析式;(2)、求两函数图象的另一个交点坐标;(3)、直接写出不等式;kx+b≤ 的解集.