四川省绵阳市2020年中考数学试卷
试卷更新日期:2020-08-17 类型:中考真卷
一、单选题
-
1. ﹣3的相反数是( )A、﹣3 B、﹣ C、 D、32. 如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
 A、2条 B、4条 C、6条 D、8条3. 近年来,华为手机越来越受到消费者的青睐.截至2019年12月底,华为5G手机全球总发货量突破690万台.将690万用科学记数法表示为( )A、0.69×107 B、69×105 C、6.9×105 D、6.9×1064. 下列四个图形中,不能作为正方体的展开图的是( )A、
A、2条 B、4条 C、6条 D、8条3. 近年来,华为手机越来越受到消费者的青睐.截至2019年12月底,华为5G手机全球总发货量突破690万台.将690万用科学记数法表示为( )A、0.69×107 B、69×105 C、6.9×105 D、6.9×1064. 下列四个图形中,不能作为正方体的展开图的是( )A、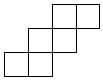 B、
B、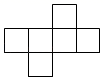 C、
C、 D、
D、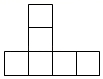 5. 若 有意义,则a的取值范围是( )A、a≥1 B、a≤1 C、a≥0 D、a≤﹣16. 《九章算术》中记载“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数、羊价各是多少?此问题中羊价为( )A、160钱 B、155钱 C、150钱 D、145钱7. 如图,在四边形ABCD中,∠A=∠C=90°,DF∥BC,∠ABC的平分线BE交DF于点G,GH⊥DF,点E恰好为DH的中点,若AE=3,CD=2,则GH=( )
5. 若 有意义,则a的取值范围是( )A、a≥1 B、a≤1 C、a≥0 D、a≤﹣16. 《九章算术》中记载“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数、羊价各是多少?此问题中羊价为( )A、160钱 B、155钱 C、150钱 D、145钱7. 如图,在四边形ABCD中,∠A=∠C=90°,DF∥BC,∠ABC的平分线BE交DF于点G,GH⊥DF,点E恰好为DH的中点,若AE=3,CD=2,则GH=( )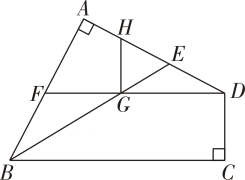 A、1 B、2 C、3 D、48. 将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率为( )A、 B、 C、 D、9. 在螳螂的示意图中,AB∥DE,△ABC是等腰三角形,∠ABC=124°,∠CDE=72°,则∠ACD=( )
A、1 B、2 C、3 D、48. 将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率为( )A、 B、 C、 D、9. 在螳螂的示意图中,AB∥DE,△ABC是等腰三角形,∠ABC=124°,∠CDE=72°,则∠ACD=( )
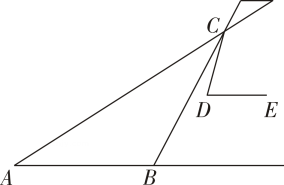 A、16° B、28° C、44° D、45°10. 甲、乙二人同驾一辆车出游,各匀速行驶一半路程,共用3小时,到达目的地后,甲对乙说:“我用你所花的时间,可以行驶180km”,乙对甲说:“我用你所花的时间,只能行驶80km”.从他们的交谈中可以判断,乙驾车的时长为( )A、1.2小时 B、1.6小时 C、1.8小时 D、2小时11. 三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A、16° B、28° C、44° D、45°10. 甲、乙二人同驾一辆车出游,各匀速行驶一半路程,共用3小时,到达目的地后,甲对乙说:“我用你所花的时间,可以行驶180km”,乙对甲说:“我用你所花的时间,只能行驶80km”.从他们的交谈中可以判断,乙驾车的时长为( )A、1.2小时 B、1.6小时 C、1.8小时 D、2小时11. 三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( ) A、4 米 B、5 米 C、2 米 D、7米12. 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=2 ,AD=2,将△ABC绕点C顺时针方向旋转后得△ ,当 恰好经过点D时,△ CD为等腰三角形,若B =2,则A =( )
A、4 米 B、5 米 C、2 米 D、7米12. 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=2 ,AD=2,将△ABC绕点C顺时针方向旋转后得△ ,当 恰好经过点D时,△ CD为等腰三角形,若B =2,则A =( )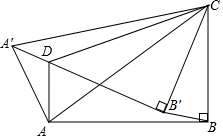 A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题
-
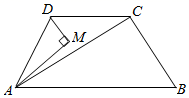
13. 因式分解:x3y﹣4xy3= .14. 平面直角坐标系中,将点A(﹣1,2)先向左平移2个单位,再向上平移1个单位后得到的点A1的坐标为 .15. 若多项式 是关于x,y的三次多项式,则 .16. 我市认真落实国家“精准扶贫”政策,计划在对口帮扶的贫困县种植甲、乙两种火龙果共100亩,根据市场调查,甲、乙两种火龙果每亩的种植成本分别为0.9万元、1.1万元,每亩的销售额分别为2万元、2.5万元,如果要求种植成本不少于98万元,但不超过100万元,且所有火龙果能全部售出,则该县在此项目中获得的最大利润是万元.(利润=销售额﹣种植成本)17. 如图,四边形ABCD中,AB∥CD,∠ABC=60°,AD=BC=CD=4,点M是四边形ABCD内的一个动点,满足∠AMD=90°,则点M到直线BC的距离的最小值为 .
 18. 若不等式 >﹣x﹣ 的解都能使不等式(m﹣6)x<2m+1成立,则实数m的取值范围是 .19. 如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数y= (k<0)的图象在第二象限交于A(﹣3,m),B(n,2)两点.
18. 若不等式 >﹣x﹣ 的解都能使不等式(m﹣6)x<2m+1成立,则实数m的取值范围是 .19. 如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数y= (k<0)的图象在第二象限交于A(﹣3,m),B(n,2)两点.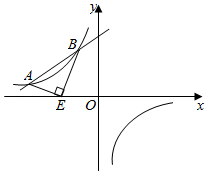 (1)、当m=1时,求一次函数的解析式;(2)、若点E在x轴上,满足∠AEB=90°,且AE=2﹣m,求反比例函数的解析式.
(1)、当m=1时,求一次函数的解析式;(2)、若点E在x轴上,满足∠AEB=90°,且AE=2﹣m,求反比例函数的解析式.三、解答题
-
20.(1)、计算:| ﹣3|+2 cos60°﹣ × ﹣(﹣ )0 .(2)、先化简,再求值:(x+2+ )÷ ,其中x= ﹣1.21. 4月23日是“世界读书日”,甲、乙两个书店在这一天举行了购书优惠活动.甲书店:所有书籍按标价8折出售;乙书店:一次购书中标价总额不超过100元的按原价计费,超过100元后的部分打6折.(1)、以x(单位:元)表示标价总额,y(单位:元)表示应支付金额,分别就两家书店的优惠方式,求y关于x的函数解析式;(2)、“世界读书日”这一天,如何选择这两家书店去购书更省钱?22. 为助力新冠肺炎疫情后经济的复苏,天天快餐公司积极投入到复工复产中.现有A、B两家农副产品加工厂到该公司推销鸡腿,两家鸡腿的价格相同,品质相近.该公司决定通过检查质量来确定选购哪家的鸡腿.检察人员从两家分别抽取100个鸡腿,然后再从中随机各抽取10个,记录它们的质量(单位:克)如表:
A加工厂
74
75
75
75
73
77
78
72
76
75
B加工厂
78
74
78
73
74
75
74
74
75
75
(1)、根据表中数据,求A加工厂的10个鸡腿质量的中位数、众数、平均数;(2)、估计B加工厂这100个鸡腿中,质量为75克的鸡腿有多少个?(3)、根据鸡腿质量的稳定性,该快餐公司应选购哪家加工厂的鸡腿?23. 如图,△ABC内接于⊙O,点D在⊙O外,∠ADC=90°,BD交⊙O于点E,交AC于点F,∠EAC=∠DCE,∠CEB=∠DCA,CD=6,AD=8. (1)、求证:AB∥CD;(2)、求证:CD是⊙O的切线;(3)、求tan∠ACB的值.24. 如图,抛物线过点A(0,1)和C,顶点为D,直线AC与抛物线的对称轴BD的交点为B( ,0),平行于y轴的直线EF与抛物线交于点E,与直线AC交于点F,点F的横坐标为 ,四边形BDEF为平行四边形.
(1)、求证:AB∥CD;(2)、求证:CD是⊙O的切线;(3)、求tan∠ACB的值.24. 如图,抛物线过点A(0,1)和C,顶点为D,直线AC与抛物线的对称轴BD的交点为B( ,0),平行于y轴的直线EF与抛物线交于点E,与直线AC交于点F,点F的横坐标为 ,四边形BDEF为平行四边形.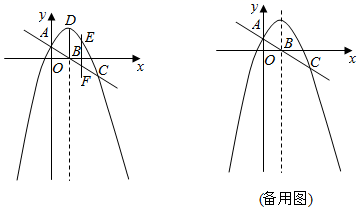 (1)、求点F的坐标及抛物线的解析式;(2)、若点P为抛物线上的动点,且在直线AC上方,当△PAB面积最大时,求点P的坐标及△PAB面积的最大值;(3)、在抛物线的对称轴上取一点Q,同时在抛物线上取一点R,使以AC为一边且以A,C,Q,R为顶点的四边形为平行四边形,求点Q和点R的坐标.25. 如图,在矩形ABCD中,对角线相交于点O,⊙M为△BCD的内切圆,切点分别为N,P,Q,DN=4,BN=6.
(1)、求点F的坐标及抛物线的解析式;(2)、若点P为抛物线上的动点,且在直线AC上方,当△PAB面积最大时,求点P的坐标及△PAB面积的最大值;(3)、在抛物线的对称轴上取一点Q,同时在抛物线上取一点R,使以AC为一边且以A,C,Q,R为顶点的四边形为平行四边形,求点Q和点R的坐标.25. 如图,在矩形ABCD中,对角线相交于点O,⊙M为△BCD的内切圆,切点分别为N,P,Q,DN=4,BN=6.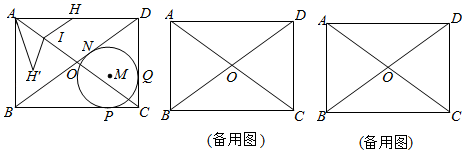 (1)、求BC,CD;(2)、点H从点A出发,沿线段AD向点D以每秒3个单位长度的速度运动,当点H运动到点D时停止,过点H作HI∥BD交AC于点I,设运动时间为t秒.
(1)、求BC,CD;(2)、点H从点A出发,沿线段AD向点D以每秒3个单位长度的速度运动,当点H运动到点D时停止,过点H作HI∥BD交AC于点I,设运动时间为t秒.①将△AHI沿AC翻折得△A I,是否存在时刻t,使点 恰好落在边BC上?若存在,求t的值;若不存在,请说明理由;
②若点F为线段CD上的动点,当△OFH为正三角形时,求t的值.