山东省东营市2020年中考数学试卷
试卷更新日期:2020-08-17 类型:中考真卷
一、单选题
-
1. -6的倒数是( ).A、6 B、 C、 D、-62. 下列运算正确的是( )A、 B、 C、 D、3. 利用科学计算器求值时,小明的按键顺序为
 ,则计算器面板显示的结果为( ) A、-2 B、2 C、±2 D、44. 如图,直线 相交于点O,射线 平分 若 ,则 等于( )
,则计算器面板显示的结果为( ) A、-2 B、2 C、±2 D、44. 如图,直线 相交于点O,射线 平分 若 ,则 等于( )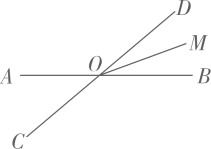 A、 B、 C、 D、5. 如图,随机闭合开关 , , 中的两个,则能让两盏灯泡同时发光的概率为( )
A、 B、 C、 D、5. 如图,随机闭合开关 , , 中的两个,则能让两盏灯泡同时发光的概率为( )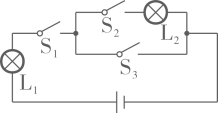 A、 B、 C、 D、6. 如图,已知抛物线 的图象与x轴交于 两点,其对称轴与x轴交于点C其中 两点的横坐标分别为-1和1下列说法错误的是( )
A、 B、 C、 D、6. 如图,已知抛物线 的图象与x轴交于 两点,其对称轴与x轴交于点C其中 两点的横坐标分别为-1和1下列说法错误的是( )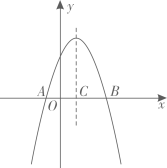 A、 B、 C、 D、当 时,y随x的增大而减小7. 用一个半径为 面积为 的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为( )A、 B、 C、2 D、18. 中国古代数学著作《算法统宗》中有这样一段记载:“ 三百七十八里关,初健步不为难,次日脚痛减一半,六朝才得到其关”其大意是:有人要去某关口,路程 里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半, 一共走了六天才到达目的地.则此人第三天走的路程为( )A、96里 B、48里 C、24里 D、12里9. 如图1,点P从 的顶点A出发,沿 匀速运动到点C,图2是点P运动时线段 的长度y随时间x变化的关系图象,其中点Q为曲线部分的最低点,则 的边 的长度为( )
A、 B、 C、 D、当 时,y随x的增大而减小7. 用一个半径为 面积为 的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为( )A、 B、 C、2 D、18. 中国古代数学著作《算法统宗》中有这样一段记载:“ 三百七十八里关,初健步不为难,次日脚痛减一半,六朝才得到其关”其大意是:有人要去某关口,路程 里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半, 一共走了六天才到达目的地.则此人第三天走的路程为( )A、96里 B、48里 C、24里 D、12里9. 如图1,点P从 的顶点A出发,沿 匀速运动到点C,图2是点P运动时线段 的长度y随时间x变化的关系图象,其中点Q为曲线部分的最低点,则 的边 的长度为( ) A、12 B、8 C、10 D、1310. 如图,在正方形 中,点P是 上一动点(不与 重合) ,对角线 相交于点O,过点P分别作 的垂线,分别交 于点 交 于点 .下列结论:① ;② ;③ ;④ ;⑤点O在 两点的连线上.其中正确的是( )
A、12 B、8 C、10 D、1310. 如图,在正方形 中,点P是 上一动点(不与 重合) ,对角线 相交于点O,过点P分别作 的垂线,分别交 于点 交 于点 .下列结论:① ;② ;③ ;④ ;⑤点O在 两点的连线上.其中正确的是( )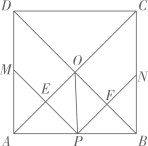 A、①②③④ B、①②③⑤ C、①②③④⑤ D、③④⑤
A、①②③④ B、①②③⑤ C、①②③④⑤ D、③④⑤二、填空题
-
11. 2020年6月23日9时43分,“北斗三号”最后一颗全球组网卫星发射成功,它的授时精度小于 秒,则 用科学记数法表示为 .12. 因式分解: .13. 某校女子排球队队员的年龄分布如下表:
年龄
13
14
15
人数
4
7
4
则该校女子排球队队员的平均年龄是岁.
14. 已知一次函数y=kx+b的图象经过A(1,﹣1),B(﹣1,3)两点,则k0(填“>”或“<”)15. 如果关于 的一元二次方程 有实数根,那么m的取值范围是 .16. 如图,P为平行四边形 边 上一点, 分别为 上的点,且 的面积分别记为 .若 则 .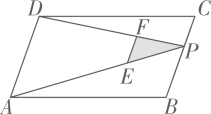 17. 如图,在 中, 的半径为1,点P是 边上的动点,过点P作 的一条切线 (其中点Q为切点),则线段 长度的最小值为 .
17. 如图,在 中, 的半径为1,点P是 边上的动点,过点P作 的一条切线 (其中点Q为切点),则线段 长度的最小值为 .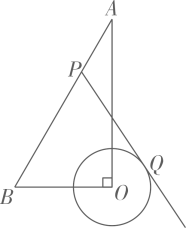 18. 如图,在平面直角坐标系中,已知直线 和双曲线 ,在直线上取一点,记为 ,过 作 轴的垂线交双曲线于点 ,过 作y轴的垂线交直线于点 ,过 作x轴的垂线交双曲线于点 ,过 作 轴的垂线交直线于点 ······,依次进行下去,记点 的横坐标为 ,若 则 .
18. 如图,在平面直角坐标系中,已知直线 和双曲线 ,在直线上取一点,记为 ,过 作 轴的垂线交双曲线于点 ,过 作y轴的垂线交直线于点 ,过 作x轴的垂线交双曲线于点 ,过 作 轴的垂线交直线于点 ······,依次进行下去,记点 的横坐标为 ,若 则 .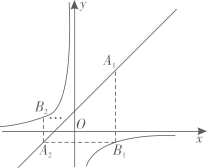
三、解答题
-
19.(1)、计算: ;(2)、先化简,再求值: ,其中 .20. 如图,在 中,以 为直径的 交 于点M弦 交 于点E,且 .
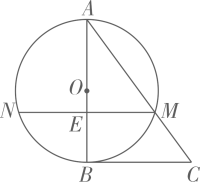 (1)、求证: 是 的切线;(2)、求 的直径 的长度.21. 如图, 处是一钻井平台,位于东营港口A的北偏东 方向上,与港口A相距 海里,一艘摩托艇从A出发,自西向东航行至B时,改变航向以每小时50海里的速度沿 方向行进,此时C位于B的北偏西 方向,则从B到达C需要多少小时?
(1)、求证: 是 的切线;(2)、求 的直径 的长度.21. 如图, 处是一钻井平台,位于东营港口A的北偏东 方向上,与港口A相距 海里,一艘摩托艇从A出发,自西向东航行至B时,改变航向以每小时50海里的速度沿 方向行进,此时C位于B的北偏西 方向,则从B到达C需要多少小时?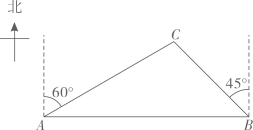 22. 东营市某中学对2020年4月份线上教学学生的作业情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.
22. 东营市某中学对2020年4月份线上教学学生的作业情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.作业情况
频数
频率
非常好
0.22
较好
68
一般
不好
40
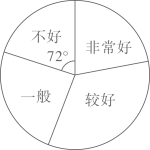
请根据图表中提供的信息,解答下列问题:
(1)、本次抽样共调查了多少名学生?(2)、将统计表中所缺的数据填在表中横线上;(3)、若该中学有1800名学生,估计该校学生作业情况“非常好”和“较好”的学生一共约多少名?(4)、某学习小组4名学生的作业本中,有2本“非常好”(记为 ), 本“较好”(记为 ),1本“一般”(记为C),这些作业本封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回, 从余下的3本中再抽取一本 ,请用“列表法”或“画树状图”的方法求出两次抽到的作业本都是“非常好”的概率.23. 2020年初,新冠肺炎疫情爆发,市场上防疫口罩热销,某医药公司每月生产甲、乙两种型号的防疫口罩共 万只,且所有口罩当月全部售出,其中成本、售价如下表:型号
价格(元/只)
项目
甲
乙
成本
12
4
售价
18
6
(1)、若该公司三月份的销售收入为300万元,求生产甲、乙两种型号的防疫口罩分别是多少万只?(2)、如果公司四月份投入成本不超过 万元,应怎样安排甲、乙两种型号防疫口罩的产量,可使该月公司所获利润最大?并求出最大利润.24. 如图,抛物线 的图象经过点 ,交x轴于点 (点A在点B左侧),连接 直线 与 轴交于点D,与 上方的抛物线交于点E,与 交于点F.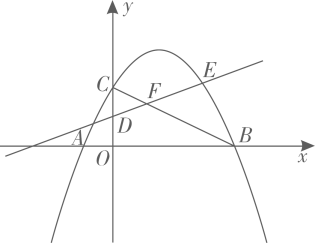 (1)、求抛物线的解析式及点 的坐标;(2)、 是否存在最大值?若存在,请求出其最大值及此时点E的坐标;若不存在,请说明理由.25. 如图1,在等腰三角形 中, 点 分别在边 上, 连接 点 分别为 的中点.
(1)、求抛物线的解析式及点 的坐标;(2)、 是否存在最大值?若存在,请求出其最大值及此时点E的坐标;若不存在,请说明理由.25. 如图1,在等腰三角形 中, 点 分别在边 上, 连接 点 分别为 的中点.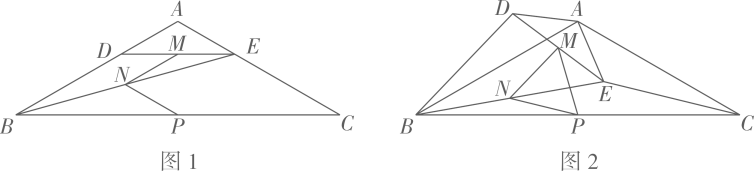 (1)、观察猜想
(1)、观察猜想图1中,线段 的数量关系是 , 的大小为;
(2)、探究证明把 绕点A顺时针方向旋转到如图2所示的位置,连接 判断 的形状,并说明理由;
(3)、拓展延伸把 绕点A在平面内自由旋转,若 ,请求出 面积的最大值.