山东省滨州市2020年中考数学试卷
试卷更新日期:2020-08-17 类型:中考真卷
一、单选题
-
1. 下列式子中,正确的是( )A、|﹣5|=﹣5 B、﹣|﹣5|=5 C、﹣(﹣5)=﹣5 D、﹣(﹣5)=5
-
2. 如图,AB//CD,点P为CD上一点,PF是∠EPC的平分线,若∠1=55°,则∠EPD的大小为( )
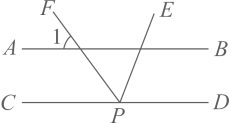 A、60° B、70° C、80° D、100°
A、60° B、70° C、80° D、100° -
3. 冠状病毒的直径约为80~120纳米,1纳米= 米,若用科学记数法表示110纳米,则正确的结果是( )A、 米 B、 米 C、 米 D、 米
-
4. 在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为( )A、 B、 C、 D、
-
5. 下列图形:线段、等边三角形、平行四边形、圆,其中既是轴对称图形,又是中心对称图形的个数为( )A、1 B、2 C、3 D、4
-
6. 如图,点A在双曲线 上,点B在双曲线 上,且AB//x轴,点C、D在x轴上,若四边形ABCD为矩形,则它的面积为( )
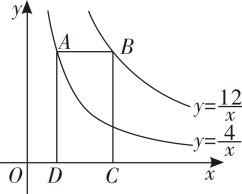 A、4 B、6 C、8 D、12
A、4 B、6 C、8 D、12 -
7. 下列命题是假命题的是( )A、对角线互相垂直且相等的平行四边形是正方形. B、对角线互相垂直的矩形是正方形. C、对角线相等的菱形是正方形. D、对角线互相垂直平分的四边形是正方形.
-
8. 已知一组数据5,4,3,4,9,关于这组数据的下列描述:
①平均数是5,②中位数是4,③众数是4,④方差是4.4,其中正确的个数为( )
A、1 B、2 C、3 D、4 -
9. 在 中,直径AB=15,弦DE⊥AB于点C.若OC:OB=3 :5,则DE的长为( )A、6 B、9 C、12 D、15
-
10. 对于任意实数k,关于x的方程 的根的情况为( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、无法判定
-
11. 对称轴为直线x=1的抛物线 (a、b、c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc<0,②b2>4ac,③4a+2b+c>0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数), ⑥当x<-1时,y随x的增大而增大,其中结论正确的个数为( )
 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6 -
12. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF;把纸片展平后再次折叠,使点A落在EF上的点 处,得到折痕BM,BM与FF相交于点N.若直线B A’交直线CD于点O,BC=5,EN=1,则OD的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
13. 若式子 在实数范围内有意义,则x的取值范围是 .
-
14. 在等腰 ABC中,AB=AC,∠B=50°,则∠A的大小为 .
-
15. 若正比例函数 的图象与某反比例函数的图象有一个交点的纵坐标是2,则该反比例函数的解析式为 .
-
16. 如图, 是正方形ABCD的内切圆,切点分别为E、F,G,H,ED与 相交于点M,则sin∠MFG的值为 .

-
17. 现有下列长度的五根木棒:3,5,8,10,13,从中任取三根,可以组成三角形的概率为 .
-
18. 若关于x的不等式组 无解,则a的取值范围为 .
-
19. 观察下列各式: , 根据其中的规律可得 (用含n的式子表示).
-
20. 如图,点P是正方形ABCD内一点,且点P到点A、B、C的距离分别为 则正方形ABCD的面积为

三、解答题
-
21. 先化简,再求值: 其中
-
22. 如图,在平面直角坐标系中,直线 与直线 相交于点P,并分别与x轴相交于点A、B.
 (1)、求交点P的坐标;(2)、求 PAB的面积;(3)、请把图象中直线 在直线 上方的部分描黑加粗,并写出此时自变量x的取值范围.
(1)、求交点P的坐标;(2)、求 PAB的面积;(3)、请把图象中直线 在直线 上方的部分描黑加粗,并写出此时自变量x的取值范围. -
23. 如图,过▱ABCD对角线AC与BD的交点E作两条互相垂直的直线,分别交边AB、BC.CD、DA于点P、M、Q、N.
 (1)、求证: PBE≌ QDE;(2)、顺次连接点P、M、Q、N,求证:四边形PMQN是菱形.
(1)、求证: PBE≌ QDE;(2)、顺次连接点P、M、Q、N,求证:四边形PMQN是菱形. -
24. 某水果商店销售一种进价为40元/千克的优质水果,若售价为50元/千克,则一个月可售出500千克;若售价在50元/千克的基础上每涨价1元,则月销售量就减少10千克.(1)、当售价为55元/千克时,每月销售水果多少千克?(2)、当月利润为8750元时,每千克水果售价为多少元?(3)、当每千克水果售价为多少元时,获得的月利润最大?
-
25. 如图,AB是 的直径,AM和BN是它的两条切线,过 上一点E作直线DC,分别交AM、BN于点D、C,且DA=DE.
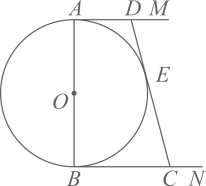 (1)、求证:直线CD是 的切线;(2)、求证:
(1)、求证:直线CD是 的切线;(2)、求证: -
26. 如图,抛物线的顶点为A(h,-1),与y轴交于点B ,点F(2,1)为其对称轴上的一个定点.
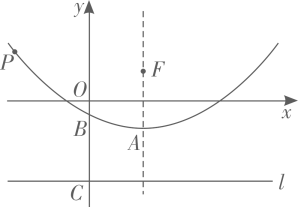 (1)、求这条抛物线的函数解析式;(2)、已知直线l是过点C(0,-3)且垂直于y轴的定直线,若抛物线上的任意一点P(m,n)到直线l的距离为d,求证:PF=d;(3)、已知坐标平面内的点D(4,3),请在抛物线上找一点Q,使△DFQ的周长最小,并求此时 DFQ周长的最小值及点Q的坐标.
(1)、求这条抛物线的函数解析式;(2)、已知直线l是过点C(0,-3)且垂直于y轴的定直线,若抛物线上的任意一点P(m,n)到直线l的距离为d,求证:PF=d;(3)、已知坐标平面内的点D(4,3),请在抛物线上找一点Q,使△DFQ的周长最小,并求此时 DFQ周长的最小值及点Q的坐标.
