内蒙古呼伦贝尔市2020年数学中考试卷
试卷更新日期:2020-08-17 类型:中考真卷
一、单选题
-
1. -2020的绝对值是( )A、-2020 B、2020 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、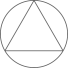 C、
C、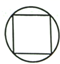 D、
D、 4. 由5个相同的小正方体组成的几何体如图所示,该几何体的俯视图是( )
4. 由5个相同的小正方体组成的几何体如图所示,该几何体的俯视图是( ) A、
A、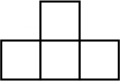 B、
B、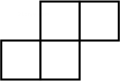 C、
C、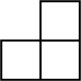 D、
D、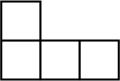 5. 下列事件是必然事件的是( )A、任意一个五边形的外角和为540° B、抛掷一枚均匀的硬币100次,正面朝上的次数为50次 C、13个人参加一个集会,他们中至少有两个人的出生月份是相同的 D、太阳从西方升起6. 如图,直线 于点E,若 ,则 的度数是( )
5. 下列事件是必然事件的是( )A、任意一个五边形的外角和为540° B、抛掷一枚均匀的硬币100次,正面朝上的次数为50次 C、13个人参加一个集会,他们中至少有两个人的出生月份是相同的 D、太阳从西方升起6. 如图,直线 于点E,若 ,则 的度数是( )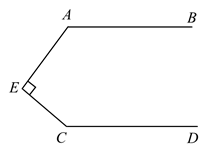 A、120° B、100° C、150° D、160°7. 已知实数a在数轴上的对应点位置如图所示,则化简 的结果是( )
A、120° B、100° C、150° D、160°7. 已知实数a在数轴上的对应点位置如图所示,则化简 的结果是( )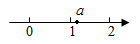 A、 B、-1 C、1 D、8. 满足不等式组 的非负整数解的个数为( )A、4 B、5 C、6 D、79. 甲、乙两人做某种机械零件,已知甲做240个零件与乙做280个零件所用的时间相等,两人每天共做130个零件.设甲每天做x个零件,下列方程正确的是( )A、 B、 C、 D、10. 如图, 的垂直平分线 交 于点D,若 ,则 的度数是( )
A、 B、-1 C、1 D、8. 满足不等式组 的非负整数解的个数为( )A、4 B、5 C、6 D、79. 甲、乙两人做某种机械零件,已知甲做240个零件与乙做280个零件所用的时间相等,两人每天共做130个零件.设甲每天做x个零件,下列方程正确的是( )A、 B、 C、 D、10. 如图, 的垂直平分线 交 于点D,若 ,则 的度数是( )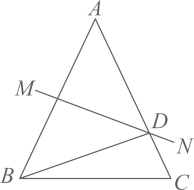 A、25° B、20° C、30° D、15°11. 如图,在 中, 分别是边 上的中线, 于点O,点 分别是 的中点,若 , ,则四边形 的周长是( )
A、25° B、20° C、30° D、15°11. 如图,在 中, 分别是边 上的中线, 于点O,点 分别是 的中点,若 , ,则四边形 的周长是( )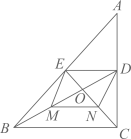 A、14 B、20 C、22 D、2812. 已知二次函数 的图象如图所示,则反比例函数 与一次函数 在同一平面直角坐标系内的图象可能是( )
A、14 B、20 C、22 D、2812. 已知二次函数 的图象如图所示,则反比例函数 与一次函数 在同一平面直角坐标系内的图象可能是( )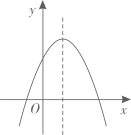 A、
A、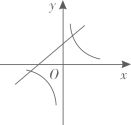 B、
B、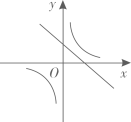 C、
C、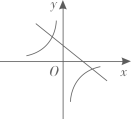 D、
D、
二、填空题
-
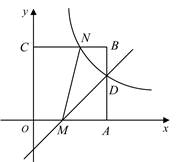
13. 中国的领水面积约为370 000 km2 , 将数370 000用科学记数法表示为: .14. 分解因式: .15. 若一个扇形的弧长是 ,面积是 ,则扇形的圆心角是度.16. 已知关于 的一元二次方程 有实数根,则m的取值范围是 .17. 如图,在平面直角坐标系中,正方形 的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的正半轴上.直线 分别与边 相交于 两点,反比例函数 的图象经过点 并与边 相交于点N,连接 .点P是直线 上的动点,当 时,点P的坐标是 .
三、解答题
-
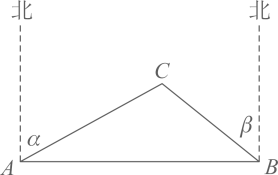
18. 计算: .19. 先化简,再求值: ,其中 .20. 两地间有一段笔直的高速铁路,长度为 .某时发生的地震对地面上以点C为圆心, 为半径的圆形区域内的建筑物有影响.分别从 两地处测得点C的方位角如图所示, .高速铁路是否会受到地震的影响.请通过计算说明理由.
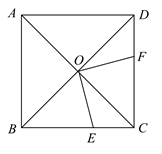
 21. 一个不透明的口袋中装有三个完全相同的小球,上面分别标有数字 ,5.(1)、从口袋中随机摸出一个小球,求摸出小球上的数字是无理数的概率(直接写出结果);(2)、先从口袋中随机摸出一个小球,将小球上的数字记为x,把小球放回口袋中并搅匀,再从口袋中随机摸出一个小球,将小球上的数字记为y.请用列表法或画树状图法求出x与y的乘积是有理数的概率.22. 已知:如图,在正方形 中,对角线 相交于点O,点 分别是边 上的点,且 .
21. 一个不透明的口袋中装有三个完全相同的小球,上面分别标有数字 ,5.(1)、从口袋中随机摸出一个小球,求摸出小球上的数字是无理数的概率(直接写出结果);(2)、先从口袋中随机摸出一个小球,将小球上的数字记为x,把小球放回口袋中并搅匀,再从口袋中随机摸出一个小球,将小球上的数字记为y.请用列表法或画树状图法求出x与y的乘积是有理数的概率.22. 已知:如图,在正方形 中,对角线 相交于点O,点 分别是边 上的点,且 .求证: .
 23. 某校为了了解初中学生每天的睡眠时间(单位为小时),随机调查了该校的部分初中学生,根据调查结果,绘制出如下统计图.
23. 某校为了了解初中学生每天的睡眠时间(单位为小时),随机调查了该校的部分初中学生,根据调查结果,绘制出如下统计图.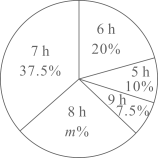
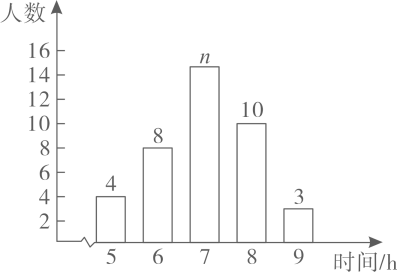
请根据相关信息,解答下列问题:
(1)、本次接受调查的初中学生人数为人,扇形统计图中的 , 条形统计图中的 ;(2)、所调查的初中学生每天睡眠时间的众数是 , 方差是;(3)、该校共有1600名初中学生,根据样本数据,估计该校初中学生每天睡眠时间不足8小时的人数.24. 如图, 是 的外接圆,直线 与 相切于点 ,连接 交 于点D. (1)、求证: 平分 ;(2)、若 的平分线 交 于点F,且 , ,求 的长.25. 某商店销售一种销售成本为每件40元的玩具,若按每件50元销售,一个月可售出500件,销售价每涨1元,月销量就减少10件.设销售价为每件x元 ,月销量为y件,月销售利润为w元.(1)、写出y与x的函数解析式和w与x的函数解析式;(2)、商店要在月销售成本不超过10000的情况下,使月销售利润达到8000元,销售价应定为每件多少元;(3)、当销售价定为每件多少元时会获得最大利润?求出最大利润.26. 如图,抛物线 与 轴交于点 和点 ,与y轴交于点C,连接 ,点P是线段 上的动点(与点 不重合),连接 并延长 交抛物线于点Q,连接 ,设点Q的横坐标为m.
(1)、求证: 平分 ;(2)、若 的平分线 交 于点F,且 , ,求 的长.25. 某商店销售一种销售成本为每件40元的玩具,若按每件50元销售,一个月可售出500件,销售价每涨1元,月销量就减少10件.设销售价为每件x元 ,月销量为y件,月销售利润为w元.(1)、写出y与x的函数解析式和w与x的函数解析式;(2)、商店要在月销售成本不超过10000的情况下,使月销售利润达到8000元,销售价应定为每件多少元;(3)、当销售价定为每件多少元时会获得最大利润?求出最大利润.26. 如图,抛物线 与 轴交于点 和点 ,与y轴交于点C,连接 ,点P是线段 上的动点(与点 不重合),连接 并延长 交抛物线于点Q,连接 ,设点Q的横坐标为m.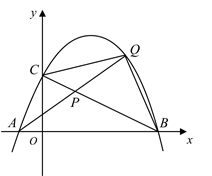 (1)、求抛物线的解析式和点C的坐标;(2)、当 的面积等于2时,求m的值;(3)、在点P运动过程中, 是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
(1)、求抛物线的解析式和点C的坐标;(2)、当 的面积等于2时,求m的值;(3)、在点P运动过程中, 是否存在最大值?若存在,求出最大值;若不存在,请说明理由.