内蒙古鄂尔多斯市2020年中考数学试卷
试卷更新日期:2020-08-17 类型:中考真卷
一、单选题
-
1. 实数﹣ 的绝对值是( )A、 B、﹣ C、﹣ D、2. 已知某物体的三视图如图所示,那么与它对应的物体是
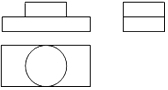 A、
A、 B、
B、 C、
C、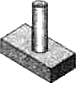 D、
D、 3. 二次根式 中,x的取值范围在数轴上表示正确的是( )A、
3. 二次根式 中,x的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列计算错误的是( )A、(﹣3ab2)2=9a2b4 B、﹣6a3b÷3ab=﹣2a2 C、(a2)3﹣(﹣a3)2=0 D、(x+1)2=x2+15. 将三角尺按如图所示放置在一张矩形纸片上,∠EGF=90°,∠FEG=30°,∠1=125°,则∠BFG的大小为( )
4. 下列计算错误的是( )A、(﹣3ab2)2=9a2b4 B、﹣6a3b÷3ab=﹣2a2 C、(a2)3﹣(﹣a3)2=0 D、(x+1)2=x2+15. 将三角尺按如图所示放置在一张矩形纸片上,∠EGF=90°,∠FEG=30°,∠1=125°,则∠BFG的大小为( )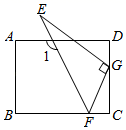 A、125° B、115° C、110° D、120°6. 一次数学测试,某小组 名同学的成绩统计如下(有两个数据被遮盖):
A、125° B、115° C、110° D、120°6. 一次数学测试,某小组 名同学的成绩统计如下(有两个数据被遮盖):组员
甲
乙
丙
丁
戊
平均成绩
众数
得分
■
■
则被遮盖的两个数据依次是( )
A、 B、 C、 D、7. 如图,在四边形ABCD中, , , , ,分别以点A,C为圆心,大于 长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,则CD的长为( )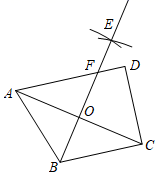 A、 B、6 C、 D、88. 下列说法正确的是( )
A、 B、6 C、 D、88. 下列说法正确的是( )① 的值大于 ;②正六边形的内角和是720°,它的边长等于半径;③从一副扑克牌中随机抽取一张,它是黑桃的概率是 ;④甲、乙两人各进行了10次射击测试,他们的平均成绩相同,方差分别是s2甲=1.3,s2乙=1.1,则乙的射击成绩比甲稳定.
A、①②③④ B、①②④ C、①④ D、②③9. 如图,四边形OAA1B1是边长为1的正方形,以对角线OA1为边作第二个正方形OA1A2B2 , 连接AA2 , 得到 AA1A2;再以对角线OA2为边作第三个正方形OA2A3B3 , 连接A1A3 , 得到 A1A2A3 , 再以对角线OA3为边作第四个正方形OA2A4B4 , 连接A2A4 , 得到 A2A3A4 , …,设 AA1A2 , A1A2A3 , A2A3A4 , …,的面积分别为S1 , S2 , S3 , …,如此下去,则S2020的值为( ) A、 B、22018 C、22018+ D、101010. 鄂尔多斯动物园内的一段线路如图1所示,动物园内有免费的班车,从入口处出发,沿该线路开往大象馆,途中停靠花鸟馆(上下车时间忽略不计),第一班车上午9:20发车,以后每隔10分钟有一班车从入口处发车,且每一班车速度均相同.小聪周末到动物园游玩,上午9点到达入口处,因还没到班车发车时间,于是从入口处出发,沿该线路步行25分钟后到达花鸟馆,离入口处的路程y(米)与时间x(分)的函数关系如图2所示,下列结论错误的是( )
A、 B、22018 C、22018+ D、101010. 鄂尔多斯动物园内的一段线路如图1所示,动物园内有免费的班车,从入口处出发,沿该线路开往大象馆,途中停靠花鸟馆(上下车时间忽略不计),第一班车上午9:20发车,以后每隔10分钟有一班车从入口处发车,且每一班车速度均相同.小聪周末到动物园游玩,上午9点到达入口处,因还没到班车发车时间,于是从入口处出发,沿该线路步行25分钟后到达花鸟馆,离入口处的路程y(米)与时间x(分)的函数关系如图2所示,下列结论错误的是( )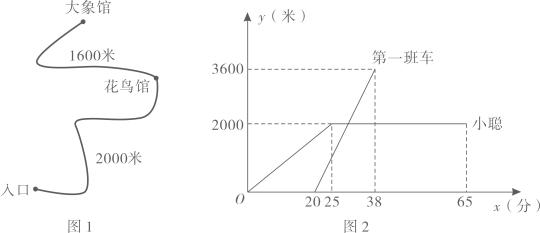 A、第一班车离入口处的距离y(米)与时间x(分)的解析式为y=200x﹣4000(20≤x≤38) B、第一班车从入口处到达花鸟馆所需的时间为10分钟 C、小聪在花鸟馆游玩40分钟后,想坐班车到大象馆,则小聪最早能够坐上第四班车 D、小聪在花鸟馆游玩40分钟后,如果坐第五班车到大象馆,那么比他在花鸟馆游玩结束后立即步行到大象馆提前了7分钟(假设小聪步行速度不变)
A、第一班车离入口处的距离y(米)与时间x(分)的解析式为y=200x﹣4000(20≤x≤38) B、第一班车从入口处到达花鸟馆所需的时间为10分钟 C、小聪在花鸟馆游玩40分钟后,想坐班车到大象馆,则小聪最早能够坐上第四班车 D、小聪在花鸟馆游玩40分钟后,如果坐第五班车到大象馆,那么比他在花鸟馆游玩结束后立即步行到大象馆提前了7分钟(假设小聪步行速度不变)二、填空题
-
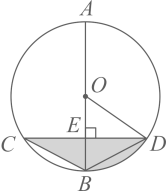
11. 截至2020年7月2日,全球新冠肺炎确诊病例已超过1051万例,其中数据1051万用科学记数法表示为 .12. 计算: +( )﹣2﹣3tan60°+(π )0= .13. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠BCD=30°,CD=2 ,则阴影部分面积S阴影= .
 14. 如图,平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为6,4,反比例函数y= (x>0)的图象经过A,B两点,若菱形ABCD的面积为2 ,则k的值为 .
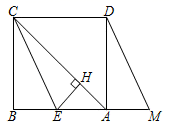
14. 如图,平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为6,4,反比例函数y= (x>0)的图象经过A,B两点,若菱形ABCD的面积为2 ,则k的值为 .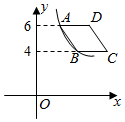 15. 如图,等边 中, ,点D、点E分别在 和 上,且 ,连接 、 交于点F,则 的最小值为 .16. 如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由 平移得到,若过点E作EH⊥AC,H为垂足,则有以下结论:
15. 如图,等边 中, ,点D、点E分别在 和 上,且 ,连接 、 交于点F,则 的最小值为 .16. 如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由 平移得到,若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;
②无论点M运动到何处,都有DM= HM;
③在点M的运动过程中,四边形CEMD可能成为菱形;
④无论点M运动到何处,∠CHM一定大于135°.
以上结论正确的有(把所有符合题意结论的序号都填上).
三、解答题
-
17.(1)、解不等式组 ,并求出该不等式组的最小整数解.(2)、先化简,再求值:( )÷ ,其中a满足a2+2a﹣15=0.18. “学而时习之,不亦说乎?”古人把经常复习当作是一种乐趣.某校为了解九年级(一)班学生每周的复习情况,班长对该班学生每周的复习时间进行了调查,复习时间四舍五入后只有4种:1小时,2小时,3小时,4小时,已知该班共有50人,根据调查结果,制作了两幅不完整的统计图表,该班女生一周的复习时间数据(单位:小时)如下:1,1,1,2,2,2,2,2,2,2,3,3,3,3,4,4,4,4,4,4
九年级(一)班女生一周复习时间频数分布表:
复习时间
频数(学生人数)
1小时
3
2小时
a
3小时
4
4小时
6
(1)、统计表中a= , 该班女生一周复习时间的中位数为小时;(2)、扇形统计图中,该班男生一周复习时间为4小时所对应圆心角的度数为°; (3)、该校九年级共有600名学生,通过计算估计一周复习时间为4小时的学生有多少名?(4)、在该班复习时间为4小时的女生中,选择其中四名分别记为A,B,C,D,为了培养更多学生对复习的兴趣,随机从该四名女生中选取两名进行班会演讲,请用树状图或者列表法求恰好选中B和D的概率.19. 如图,一次函数y=kx+b的图象分别与反比例函数y= 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(3)、该校九年级共有600名学生,通过计算估计一周复习时间为4小时的学生有多少名?(4)、在该班复习时间为4小时的女生中,选择其中四名分别记为A,B,C,D,为了培养更多学生对复习的兴趣,随机从该四名女生中选取两名进行班会演讲,请用树状图或者列表法求恰好选中B和D的概率.19. 如图,一次函数y=kx+b的图象分别与反比例函数y= 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.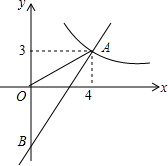 (1)、求函数y=kx+b和y= 的表达式;(2)、已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.20. 图1是挂墙式淋浴花洒的实物图,图2是抽象出来的几何图形.为使身高175cm的人能方便地淋浴,应当使旋转头固定在墙上的某个位置O,花洒的最高点B与人的头顶的铅垂距离为15cm,已知龙头手柄OA长为10cm,花洒直径AB是8cm,龙头手柄与墙面的较小夹角∠COA=26°,∠OAB=146°,则安装时,旋转头的固定点O与地面的距离应为多少?(计算结果精确到1cm,参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
(1)、求函数y=kx+b和y= 的表达式;(2)、已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.20. 图1是挂墙式淋浴花洒的实物图,图2是抽象出来的几何图形.为使身高175cm的人能方便地淋浴,应当使旋转头固定在墙上的某个位置O,花洒的最高点B与人的头顶的铅垂距离为15cm,已知龙头手柄OA长为10cm,花洒直径AB是8cm,龙头手柄与墙面的较小夹角∠COA=26°,∠OAB=146°,则安装时,旋转头的固定点O与地面的距离应为多少?(计算结果精确到1cm,参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)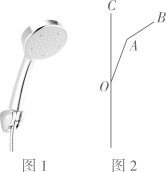 21. 我们知道,顶点坐标为(h,k)的抛物线的解析式为y=a(x﹣h)2+k(a≠0).今后我们还会学到,圆心坐标为(a,b),半径为r的圆的方程(x﹣a)2+(y﹣b)2=r2 , 如:圆心为P(﹣2,1),半径为3的圆的方程为(x+2)2+(y﹣1)2=9.
21. 我们知道,顶点坐标为(h,k)的抛物线的解析式为y=a(x﹣h)2+k(a≠0).今后我们还会学到,圆心坐标为(a,b),半径为r的圆的方程(x﹣a)2+(y﹣b)2=r2 , 如:圆心为P(﹣2,1),半径为3的圆的方程为(x+2)2+(y﹣1)2=9.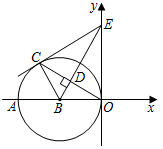 (1)、以M(﹣3,﹣1)为圆心, 为半径的圆的方程为 .(2)、如图,以B(﹣3,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC,垂足为D,延长BD交y轴于点E,已知sin∠AOC= .
(1)、以M(﹣3,﹣1)为圆心, 为半径的圆的方程为 .(2)、如图,以B(﹣3,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC,垂足为D,延长BD交y轴于点E,已知sin∠AOC= .①连接EC,证明:EC是⊙B的切线;
②在BE上是否存在一点Q,使QB=QC=QE=QO?若存在,求点Q的坐标,并写出以Q为圆心,以QB为半径的⊙Q的方程;若不存在,请说明理由.
22. 某水果店将标价为10元/斤的某种水果.经过两次降价后,价格为8.1元/斤,并且两次降价的百分率相同.(1)、求该水果每次降价的百分率;(2)、从第二次降价的第1天算起,第x天(x为整数)的销量及储藏和损耗费用的相关信息如下表所示:时间(天)
x
销量(斤)
120﹣x
储藏和损耗费用(元)
3x2﹣64x+400
已知该水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<10)之间的函数解析式,并求出第几天时销售利润最大,最大利润是多少?
23. 如图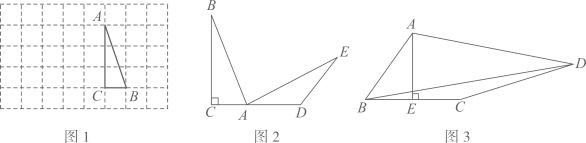 (1)、(操作发现)
(1)、(操作发现)如图1,在边长为1个单位长度的小正方形组成的网格中, 的三个顶点均在格点上.
①请按要求画图:将 绕点A顺时针方向旋转90°,点B的对应点为点 ,点C的对应点为点 .连接 ;
②在①中所画图形中, =°.
(2)、(问题解决)如图2,在 中,BC=1,∠C=90°,延长CA到D,使CD=1,将斜边AB绕点A顺时针旋转90°到AE,连接DE,求∠ADE的度数.
(3)、(拓展延伸)如图3,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=1,CD=3,AD=kAB(k为常数),求BD的长(用含k的式子表示).
24. 如图1,抛物线y=x2+bx+c交x轴于A,B两点,其中点A的坐标为(1,0),与y轴交于点C((0,﹣3). (1)、求抛物线的函数解析式;(2)、点D为y轴上一点,如果直线BD与直线BC的夹角为15°,求线段CD的长度;(3)、如图2,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO,求点P的坐标.
(1)、求抛物线的函数解析式;(2)、点D为y轴上一点,如果直线BD与直线BC的夹角为15°,求线段CD的长度;(3)、如图2,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO,求点P的坐标.