湖南省永州市2020年中考数学试卷
试卷更新日期:2020-08-17 类型:中考真卷
一、单选题
-
1. -2020的相反数为( )A、 B、2020 C、-2020 D、2. 永州市教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手开展安全教育.下列安全图标不是轴对称的是( )A、
 B、
B、 C、
C、 D、
D、 3. 永州市现有户籍人口约635.3万人,则“现有户籍人口数”用科学记数法表示正确的是( )A、 人 B、 人 C、 人 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 已知一组数据1,2,8,6,8对这组数据描述正确的是( )A、众数是8 B、平均数是6 C、中位数是8 D、方差是96. 如图,已知 .能直接判断 的方法是( )
3. 永州市现有户籍人口约635.3万人,则“现有户籍人口数”用科学记数法表示正确的是( )A、 人 B、 人 C、 人 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 已知一组数据1,2,8,6,8对这组数据描述正确的是( )A、众数是8 B、平均数是6 C、中位数是8 D、方差是96. 如图,已知 .能直接判断 的方法是( ) A、 B、 C、 D、7. 如图,已知 是 的两条切线,A , B为切点,线段 交 于点M . 给出下列四种说法:① ;② ;③四边形 有外接圆;④M是 外接圆的圆心,其中正确说法的个数是( )
A、 B、 C、 D、7. 如图,已知 是 的两条切线,A , B为切点,线段 交 于点M . 给出下列四种说法:① ;② ;③四边形 有外接圆;④M是 外接圆的圆心,其中正确说法的个数是( )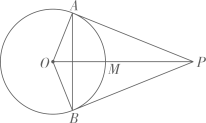 A、1 B、2 C、3 D、48. 如图,在 中, ,四边形 的面积为21,则 的面积是( )
A、1 B、2 C、3 D、48. 如图,在 中, ,四边形 的面积为21,则 的面积是( )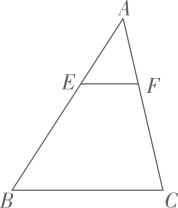 A、 B、25 C、35 D、639. 如图,这是一个底面为等边三角形的正三棱柱和它的主视图、俯视图,则它的左视图的面积是( )
A、 B、25 C、35 D、639. 如图,这是一个底面为等边三角形的正三棱柱和它的主视图、俯视图,则它的左视图的面积是( )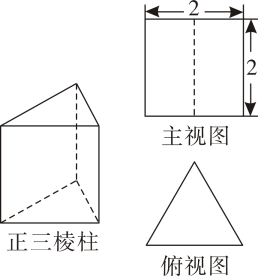 A、4 B、2 C、 D、10. 已知点 和直线 ,求点P到直线 的距离d可用公式 计算.根据以上材料解决下面问题:如图, 的圆心C的坐标为 ,半径为1,直线l的表达式为 ,P是直线l上的动点,Q是 上的动点,则 的最小值是( )
A、4 B、2 C、 D、10. 已知点 和直线 ,求点P到直线 的距离d可用公式 计算.根据以上材料解决下面问题:如图, 的圆心C的坐标为 ,半径为1,直线l的表达式为 ,P是直线l上的动点,Q是 上的动点,则 的最小值是( ) A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
11. 在函数 中,自变量x的取值范围是 .12. 方程组 的解是 .13. 若关于x的一元二次方程x2﹣4x﹣m=0有两个不相等的实数根,则实数m的取值范围是 .
14. 永州市教育部门为了了解全市中小学安全教育情况,对某校进行了“防溺水”安全知识的测试.从七年级随机抽取了50名学生的测试成绩(百分制),整理样本数据,得到下表:成绩 90≤x≤100 80≤x<90 70≤x<80 60≤x<70 x<60 人数 25 15 5 4 1 根据抽样调查结果,估计该校七年级600名学生中,80分(含80分)以上的学生有人.
15. 已知圆锥的底面周长是 分米,母线长为1分米,则圆锥的侧面积是平方分米.16. 已知直线 ,用一块含30°角的直角三角板按图中所示的方式放置,若 ,则 .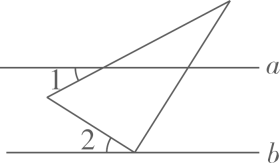 17. 如图,正比例函数 与反比例函数 的图象交于A , C两点,过点A作 轴于点B , 过点C作 轴于点D , 则 的面积为 .
17. 如图,正比例函数 与反比例函数 的图象交于A , C两点,过点A作 轴于点B , 过点C作 轴于点D , 则 的面积为 .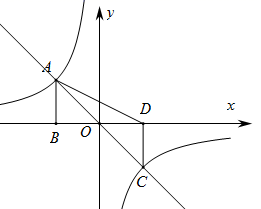 18. 在平面直角坐标系中的位置如图所示,且 ,在 内有一点 ,M , N分别是 边上的动点,连接 ,则 周长的最小值是 .
18. 在平面直角坐标系中的位置如图所示,且 ,在 内有一点 ,M , N分别是 边上的动点,连接 ,则 周长的最小值是 .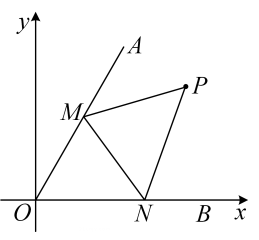
三、解答题
-
19. 计算: .20. 先化简,再求值: ,其中 .21. 今年6月份,永州市某中学开展“六城同创”知识竞赛活动.赛后,随机抽取了部分参赛学生的成绩,按得分划为A , B , C , D四个等级,A: ,B: ,C: ,D: ,并绘制了如下两幅不完整的统计图,请结合图中所给信息,解答下列问题:
 (1)、请把条形统计图补充完整.(2)、扇形统计图中 , , B等级所占扇形的圆心角度数为 .(3)、该校准备从上述获得A等级的四名学生中选取两人参加永州市举行的“六城同创”知识竞赛,已知这四人中有两名男生(用 , 表示),两名女生(用 , 表示),请利用树状图法或列表法,求恰好抽到1名男生和1名女生的概率.22. 一艘渔船从位于A海岛北偏东60°方向,距A海岛60海里的B处出发,以每小时30海里的速度沿正南方向航行.已知在A海岛周围50海里水域内有暗礁.(参考数据: )
(1)、请把条形统计图补充完整.(2)、扇形统计图中 , , B等级所占扇形的圆心角度数为 .(3)、该校准备从上述获得A等级的四名学生中选取两人参加永州市举行的“六城同创”知识竞赛,已知这四人中有两名男生(用 , 表示),两名女生(用 , 表示),请利用树状图法或列表法,求恰好抽到1名男生和1名女生的概率.22. 一艘渔船从位于A海岛北偏东60°方向,距A海岛60海里的B处出发,以每小时30海里的速度沿正南方向航行.已知在A海岛周围50海里水域内有暗礁.(参考数据: )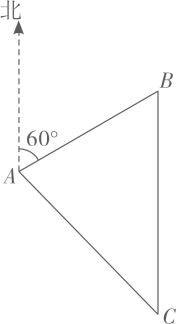 (1)、这艘渔船在航行过程中是否有触礁的危险?请说明理由.(2)、渔船航行3小时后到达C处,求A , C之间的距离.23. 某药店在今年3月份,购进了一批口罩,这批口罩包括有一次性医用外科口罩和N95口罩,且两种口罩的只数相同.其中购进一次性医用外科口罩花费1600元,N95口罩花费9600元.已知购进一次性医用外科口罩的单价比N95口罩的单价少10元.(1)、求该药店购进的一次性医用外科口罩和N95口罩的单价各是多少元?(2)、该药店计划再次购进两种口罩共2000只,预算购进的总费用不超过1万元,问至少购进一次性医用外科口罩多少只?24. 如图, 内接于 是 的直径, 与 相切于点B , 交 的延长线于点D , E为 的中点,连接 .
(1)、这艘渔船在航行过程中是否有触礁的危险?请说明理由.(2)、渔船航行3小时后到达C处,求A , C之间的距离.23. 某药店在今年3月份,购进了一批口罩,这批口罩包括有一次性医用外科口罩和N95口罩,且两种口罩的只数相同.其中购进一次性医用外科口罩花费1600元,N95口罩花费9600元.已知购进一次性医用外科口罩的单价比N95口罩的单价少10元.(1)、求该药店购进的一次性医用外科口罩和N95口罩的单价各是多少元?(2)、该药店计划再次购进两种口罩共2000只,预算购进的总费用不超过1万元,问至少购进一次性医用外科口罩多少只?24. 如图, 内接于 是 的直径, 与 相切于点B , 交 的延长线于点D , E为 的中点,连接 . (1)、求证: 是 的切线.(2)、已知 ,求O , E两点之间的距离.25. 在平面直角坐标系 xOy 中,等腰直角 的直角顶点C在y轴上,另两个顶点A , B在x轴上,且 ,抛物线经过A , B , C三点,如图1所示.
(1)、求证: 是 的切线.(2)、已知 ,求O , E两点之间的距离.25. 在平面直角坐标系 xOy 中,等腰直角 的直角顶点C在y轴上,另两个顶点A , B在x轴上,且 ,抛物线经过A , B , C三点,如图1所示.
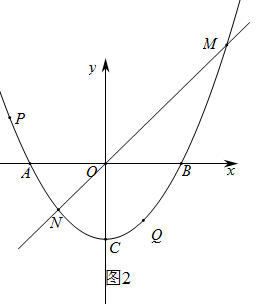 (1)、求抛物线所表示的二次函数表达式.(2)、过原点任作直线l交抛物线于M , N两点,如图2所示.
(1)、求抛物线所表示的二次函数表达式.(2)、过原点任作直线l交抛物线于M , N两点,如图2所示.①求 面积的最小值.
②已知 是抛物线上一定点,问抛物线上是否存在点P , 使得点P与点Q关于直线l对称,若存在,求出点P的坐标及直线l的一次函数表达式;若不存在,请说明理由.
26. 某校开展了一次综合实践活动,参加该活动的每个学生持有两张宽为 ,长足够的矩形纸条.探究两张纸条叠放在一起,重叠部分的形状和面积.如图1所示,一张纸条水平放置不动,另一张纸条与它成45°的角,将该纸条从右往左平移.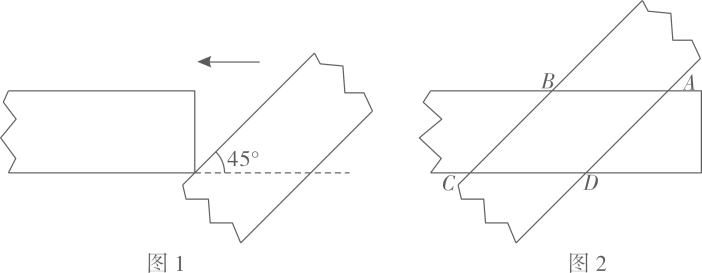 (1)、写出在平移过程中,重叠部分可能出现的形状.(2)、当重叠部分的形状为如图2所示的四边形 时,求证:四边形 是菱形.(3)、设平移的距离为 ,两张纸条重叠部分的面积为 .求s与x的函数关系式,并求s的最大值.
(1)、写出在平移过程中,重叠部分可能出现的形状.(2)、当重叠部分的形状为如图2所示的四边形 时,求证:四边形 是菱形.(3)、设平移的距离为 ,两张纸条重叠部分的面积为 .求s与x的函数关系式,并求s的最大值.