湖南省益阳市2020年中考数学试卷
试卷更新日期:2020-08-17 类型:中考真卷
一、单选题
-
1. 四个实数1,0, ,-3中,最大的是( )A、1 B、0 C、 D、-32. 将不等式组 的解集在数轴上表示,正确的是( )A、
 B、
B、 C、
C、 D、
D、 3. 图所示的几何体的俯视图是( )
3. 图所示的几何体的俯视图是( )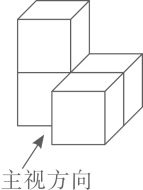 A、
A、 B、
B、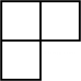 C、
C、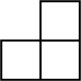 D、
D、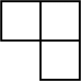 4. 一组数据由4个数组成,其中3个数分别为2,3,4,且这组数据的平均数为4,则这组数据的中位数为( )A、7 B、4 C、3.5 D、35. 同时满足二元一次方程 和 的x,y的值为( )A、 B、 C、 D、6. 下列因式分解正确的是( )A、 B、 C、 D、7. 一次函数 的图象如图所示,则下列结论正确的是( )
4. 一组数据由4个数组成,其中3个数分别为2,3,4,且这组数据的平均数为4,则这组数据的中位数为( )A、7 B、4 C、3.5 D、35. 同时满足二元一次方程 和 的x,y的值为( )A、 B、 C、 D、6. 下列因式分解正确的是( )A、 B、 C、 D、7. 一次函数 的图象如图所示,则下列结论正确的是( )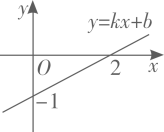 A、 B、 C、 随 的增大而减小 D、当 时,8. 如图, 的对角线 , 交于点O,若 , ,则 的长可能是( )
A、 B、 C、 随 的增大而减小 D、当 时,8. 如图, 的对角线 , 交于点O,若 , ,则 的长可能是( )
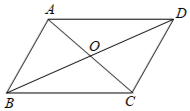 A、10 B、8 C、7 D、69. 如图,在 中, 的垂直平分线交 于点D, 平分 ,若 ,则 的度数为( )
A、10 B、8 C、7 D、69. 如图,在 中, 的垂直平分线交 于点D, 平分 ,若 ,则 的度数为( )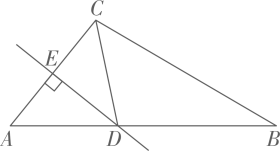 A、 B、 C、 D、10. 如图,在矩形 中,E是 上的一点, 是等边三角形, 交 于点F,则下列结论不成立的是( )
A、 B、 C、 D、10. 如图,在矩形 中,E是 上的一点, 是等边三角形, 交 于点F,则下列结论不成立的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 我国北斗全球导航系统最后一颗组网卫星于2020年6月30日成功定位于距离地球36000千米的地球同步轨道,将 用科学记数法表示为 .
 12. 如图, , , ,则 的度数为 .
12. 如图, , , ,则 的度数为 .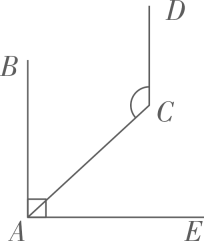 13. 小明家有一个如图所示的闹钟,他观察圆心角 ,测得 的长为 ,则 的长为 .
13. 小明家有一个如图所示的闹钟,他观察圆心角 ,测得 的长为 ,则 的长为 .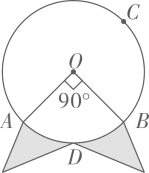 14. 若反比例函数y= 的图象经过点(﹣2,3),则k= .15. 时光飞逝,十五六岁的我们,童年里都少不了“弹珠”。小朋友甲的口袋中有 粒弹珠,其中 粒红色, 粒绿色,他随机拿出 颗送给小朋友乙,则送出的弹珠颜色为红色的概率是 .
14. 若反比例函数y= 的图象经过点(﹣2,3),则k= .15. 时光飞逝,十五六岁的我们,童年里都少不了“弹珠”。小朋友甲的口袋中有 粒弹珠,其中 粒红色, 粒绿色,他随机拿出 颗送给小朋友乙,则送出的弹珠颜色为红色的概率是 . 16. 若一个多边形的内角和是 ,则该多边形的边数是.17. 若计算 的结果为正整数,则无理数m的值可以是 . (写出一个符合条件的即可)18. 某公司新产品上市30天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是元.
16. 若一个多边形的内角和是 ,则该多边形的边数是.17. 若计算 的结果为正整数,则无理数m的值可以是 . (写出一个符合条件的即可)18. 某公司新产品上市30天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是元.
三、解答题
-
19. 计算:20. 先化简,再求值: ,其中21. 如图, 是 的半径,过点M作 的切线 ,且 , , 分别交 于点C,D,求证:
 22. 为了了解现行简化汉字的笔画画数情况,某同学随机选取语文课本的一篇文章,对其部分文字的笔画数进行统计,结果如下表:
22. 为了了解现行简化汉字的笔画画数情况,某同学随机选取语文课本的一篇文章,对其部分文字的笔画数进行统计,结果如下表:笔画数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
字数
4
8
10
16
14
20
24
36
16
14
11
9
10
7
1
请解答下列问题:
(1)、被统计汉字笔画数的众数是多少?(2)、该同学将数据进行整理,按如下方案分组统计,并制作扇形统计图:分组
笔画数 (画)
字数(个)
A组
22
B组
m
C组
76
D组
n
E组
18
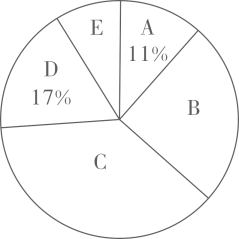
请确定上表中m、n的值及扇形统计图中组对应扇形圆心角的度数.
(3)、若这篇文章共有3500个汉字,估计笔画数在 画( 组)的字数有多少个?23. 沿江大堤经过改造后的某处横断面为如图所示的梯形 ,高 米,斜坡 的坡度 ,此处大堤的正上方有高压电线穿过, 表示高压线上的点与堤面 的最近距离(P、D、H在同一直线上),在点C处测得 . (1)、求斜坡 的坡角(2)、电力部门要求此处高压线离堤面 的安全距离不低于18米,请问此次改造是否符合电力部门的安全要求?(参考数据: , , , )24. “你怎么样,中国便是怎么样:你若光明,中国便不黑暗”。2019年,一场新冠肺炎疫情牵扯着人们的心灵,各界人士齐心协力,众志成城。针对资源急需问题,某医疗设备公司紧急复工,但受疫情影响,医用防护服生产车间仍有 人不能到厂生产,为了应对疫情,已复产的工人加班生产,由原来每天工作8小时增加到10小时,每小时完成的工作量不变原来每天能生产防护服800套,现在每天能生产防护服650套.
(1)、求斜坡 的坡角(2)、电力部门要求此处高压线离堤面 的安全距离不低于18米,请问此次改造是否符合电力部门的安全要求?(参考数据: , , , )24. “你怎么样,中国便是怎么样:你若光明,中国便不黑暗”。2019年,一场新冠肺炎疫情牵扯着人们的心灵,各界人士齐心协力,众志成城。针对资源急需问题,某医疗设备公司紧急复工,但受疫情影响,医用防护服生产车间仍有 人不能到厂生产,为了应对疫情,已复产的工人加班生产,由原来每天工作8小时增加到10小时,每小时完成的工作量不变原来每天能生产防护服800套,现在每天能生产防护服650套. (1)、求原来生产防护服的工人有多少人?(2)、复工10天后,未到的工人同时到岗加入生产,每天生产时间仍然为10小时公司决定将复工后生产的防护服14500套捐献给某地,则至少还需要生产多少天才能完成任务?25. 如图,在平面直角坐标系中,点F的坐标是 ,点P为一个动点,过点P作x轴的垂线 ,垂足为H,点P在运动过程中始终满足 (提示:平面直角坐标系内点M、N的坐标分别为 、 ,则 )
(1)、求原来生产防护服的工人有多少人?(2)、复工10天后,未到的工人同时到岗加入生产,每天生产时间仍然为10小时公司决定将复工后生产的防护服14500套捐献给某地,则至少还需要生产多少天才能完成任务?25. 如图,在平面直角坐标系中,点F的坐标是 ,点P为一个动点,过点P作x轴的垂线 ,垂足为H,点P在运动过程中始终满足 (提示:平面直角坐标系内点M、N的坐标分别为 、 ,则 )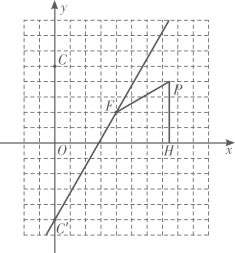 (1)、判断点P在运动过程中是否经过点C(0,5)(2)、设动点P的坐标为 ,求y关于x的函数表达式:填写下表,并在给定坐标系中画出函数的图象:
(1)、判断点P在运动过程中是否经过点C(0,5)(2)、设动点P的坐标为 ,求y关于x的函数表达式:填写下表,并在给定坐标系中画出函数的图象:x
...
0
2
4
6
8
...
y
...
...
(3)、点C关于x轴的对称点为 ,点P在直线 的下方时,求线段 长度的取值范围26. 定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形,根据以上定义,解决下列问题: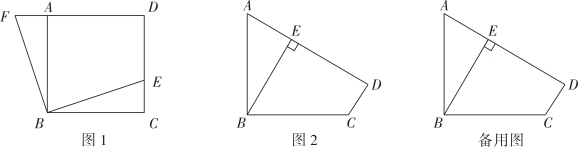 (1)、如图1,正方形 中,E是 上的点,将 绕B点旋转,使 与 重合,此时点E的对应点F在 的延长线上,则四边形 为“直等补”四边形,为什么?(2)、如图2,已知四边形 是“直等补”四边形, , , ,点 到直线 的距离为 .
(1)、如图1,正方形 中,E是 上的点,将 绕B点旋转,使 与 重合,此时点E的对应点F在 的延长线上,则四边形 为“直等补”四边形,为什么?(2)、如图2,已知四边形 是“直等补”四边形, , , ,点 到直线 的距离为 .①求 的长.
②若M、N分别是 、 边上的动点,求 周长的最小值.