天津市东丽区2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2020-08-17 类型：期末考试

进入出卷网下载

一、单选题

1. 16的算术平方根是（　　）

A、 4 B、﹣4 C、±4 D、2

查看试题解析
2. 在平面直角坐标系中，点 $P (- 1 ， - 2)$ 位于 $($ 　　 $)$

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 实数 $\sqrt{4}$ ，- $\frac{22}{7}$ ，π，0中，为无理数的是（）

A、 $\sqrt{4}$ B、- $\frac{22}{7}$ C、π D、0

查看试题解析
4. 若a＞b，则下列式子正确的是（）

A、﹣4a＞﹣4b B、 $\frac{1}{2}$ a＜ $\frac{1}{2}$ b C、4﹣a＞4﹣b D、a﹣4＞b﹣4

查看试题解析
5. 在平面直角坐标系中，点P（x+1，x-2）在x轴上，则点P的坐标是（）

A、（3，0） B、（0，-3） C、（0，-1） D、（-1，0）

查看试题解析
6. 为了解校区七年级400名学生的身高，从中抽取50名学生进行测量，下列说法正确的是（）

A、400名学生是总体 B、每个学生是个体 C、抽取的50名学生是一个样本 D、每个学生的身高是个体

查看试题解析
7. 下列说法正确的个数有（）
①同位角相等②过一点有且只有一条直线与已知直线垂直③过一点有且只有一条直线与已知直线平行④若a∥b，b∥c，则a∥c．

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，点E在 $B C$ 的延长线上，则下列条件中，不能判定 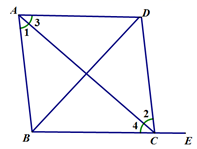$A B // C D$ 的是（）

A、 $∠ 3 = ∠ 4$ B、 $∠ A B C = ∠ D C E$ C、 $∠ 1 = ∠ 2$ D、 $∠ A D C + ∠ D A B = 180 °$

查看试题解析
9. 若方程（a-5）x^|a|-4+5y=1是关于x ， y的二元一次方程，则a的值为（）

A、 $- 5$ B、 $\pm 5$ C、 $\pm 4$ D、5

查看试题解析
10. 用不等式表示：“ $a$ 的 $\frac{1}{2}$ 与 $b$ 的和为正数”，正确的是（）

A、 $\frac{1}{2} a + b > 0$ B、 $\frac{1}{2} (a + b) > 0$ C、 $\frac{1}{2} a + b ⩾ 0$ D、 $\frac{1}{2} (a + b) ⩾ 0$

查看试题解析
11. 二元一次方程组 ${\begin{array}{l} x - 2 y = 3, \\ x + y = 6 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 1, \\ y = 5. \end{array}$ B、 ${\begin{array}{l} x = 3, \\ y = 0. \end{array}$ C、 ${\begin{array}{l} x = 4, \\ y = 2. \end{array}$ D、 ${\begin{array}{l} x = 5, \\ y = 1. \end{array}$

查看试题解析
12. 已知三个非负数a、b、c满足 $3 a + 2 b + c = 5 ， 2 a + b - 3 c = 1 ，$ 若 $m = 3 a + b - 7 c$ ，则 $m$ 的最小值为（）

A、 $- \frac{1}{11}$ B、 $- \frac{5}{7}$ C、 $- \frac{7}{8}$ D、－1

查看试题解析

二、填空题

13. 比较大小： $\sqrt{5}$ 2（填“＞”或“＜”或“=”）

查看试题解析
14. 已知关于x，y的二元一次方程mx-2y=2的一组解为 ${\begin{matrix} x = 3 \\ y = 5 \end{matrix}$ ，则m= ．

查看试题解析
15. 已知点P的坐标为(-5，-8)，那么该点P到x轴的距离为．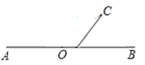

查看试题解析
16. 如图，过直线 $A B$ 上一点 $O$ 画射线 $O C ， ∠ B O C = 45 °$ ，则 $∠ A O C$ 的度数为．

查看试题解析
17. 若关于 $x$ 的不等式 $(a - 2) x > a - 2$ 的解集为 $x < 1$ ，化简 $| a - 3 | =$ .

查看试题解析
18. 如图，平面直角坐标系中，一个点从原点O出发，按向右→向上→向右→向下的顺序依次不断移动，每次移动1个单位，其移动路线如图所示，第1次移到点A₁ ，第二次移到点A₂ ，第三次移到点A₃ ， …，第n次移到点A_n ，则点A₂₀₁₉的坐标是.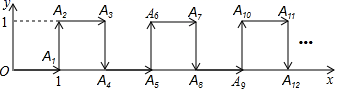

查看试题解析

三、解答题

19. 计算

(1)、 $\sqrt{16} + 2 \times \sqrt{9} - \sqrt[3]{27}$

(2)、 $| 1 - \sqrt{2} | + \sqrt{4} - \sqrt[3]{- 8}$ ；

查看试题解析
20. 2019年某市创建文明城市期间，某区教育局为了了解全区中学生对课外体育运动项目的喜欢程度，随机抽取了某校七年级部分学生进行问卷调查（每人限选一种体育运动项目）．如图是整理数据后绘制的两幅不完整的统计图，请你根据图中提供的信息，解答下列问题：

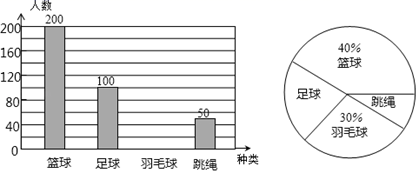(1)、这次活动一共调查了名学生；

(2)、在扇形统计图中，“跳绳”所在扇形圆心角等于度；

(3)、补全条形统计图；

(4)、若该校有七年级学生1000人，请你估计该校喜欢“足球”的学生约有多少人？．

查看试题解析
21. 求不等式组 ${\begin{array}{l} 2 x - 1 \leq 1 \\ 3 x - 3 < 4 x \end{array}$ 的整数解．

查看试题解析
22. 如图，已知四边形ABCD中， $∠ D = 100^{°} ， A C$ 平分 $∠ B A D$ ，且∠ACB=40°，∠BAC=70°．

(1)、AD与BC平行吗？试写出推理过程；

(2)、求 $∠ D A C$ 和 $∠ E A D$ 的度数．

查看试题解析
23. 某校计划购买一批篮球和足球，已知购买2个篮球和1个足球共需320元，购买3个篮球和2个足球共需540元．

(1)、求每个篮球和每个足球的售价；

(2)、如果学校计划购买这两种球共50个，总费用不超过5500元，那么最多可购买多少个足球？

查看试题解析
24. 已知方程组 ${\begin{array}{l} 2 x + y = 1 + 3 m \\ x + 2 y = 1 - m \end{array}$ 的解x、y满足x+y＜1，且m为非负数，求m的取值范围.

查看试题解析
25. 如图，在平面直角坐标系中，A(a，0)，B(b，0)，C(﹣1，2)，且（a+2）²+ $\sqrt{b - 3}$ ＝0，

(1)、求a，b的值；

(2)、在坐标轴上存在一点M，使△COM的面积是△ABC的面积的一半，求出点M的坐标．

(3)、如图2，过点C做CD⊥y轴交y轴于点D，点P为线段CD延长线上一动点，连接OP，OE平分角∠AOP，OF⊥OE，当点P运动时， $\frac{∠ O P D}{∠ D O E}$ 的值是否会改变？若不变，求其值；若改变，说明理由．

查看试题解析