初中数学浙教版九年级上册第3章 圆的基本性质 单元检测(基础篇)
试卷更新日期:2020-08-16 类型:单元试卷
一、单选题
-
1. 下列说法错误的是( )A、等弧所对的圆心角相等 B、弧的度数等于该弧所对的圆心角的度数 C、经过三点可以作一个圆 D、三角形的外心到三角形各顶点距离相等2. 过A,B,C三点能确定一个圆的条件是( )
①AB=2,BC=3,AC=5;②AB=3, BC=3,AC=2;③AB=3,BC=4,AC= 5.
A、①② B、①②③ C、②③ D、①③3. 如图,在新型俄罗斯方块游戏中(出现的图案可进行顺时针、逆时针旋转;向左、向右平移),已拼好的图案如图3所示,现又出现一个形如“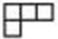 ”的方块正向下运动,你必须进行以下哪项操作,才能拼成一个完整的图形( ).
”的方块正向下运动,你必须进行以下哪项操作,才能拼成一个完整的图形( ).  A、顺时针旋转90°,向右平移 B、逆时针旋转90°,向右平移 C、顺时针旋转90°,向左平移 D、逆时针旋转90°,向左平移4. 如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )
A、顺时针旋转90°,向右平移 B、逆时针旋转90°,向右平移 C、顺时针旋转90°,向左平移 D、逆时针旋转90°,向左平移4. 如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )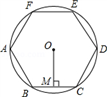 A、2, B、2 ,π C、 , D、2 ,5. 《九章算术》是我国古代著名数学著作,书中记载:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥DC于E,ED=1寸,AB=10寸,求直径CD的长。”则CD为( )
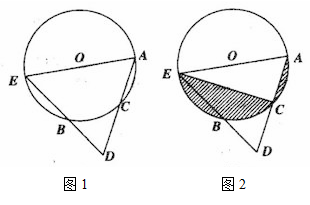
A、2, B、2 ,π C、 , D、2 ,5. 《九章算术》是我国古代著名数学著作,书中记载:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥DC于E,ED=1寸,AB=10寸,求直径CD的长。”则CD为( )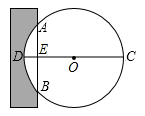 A、10寸 B、3寸 C、20寸 D、26寸6. 如图,三角形与⊙O叠合得到三条相等的弦AB、CD、EF,则以下结论正确的是( )
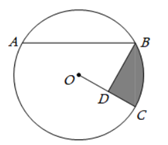
A、10寸 B、3寸 C、20寸 D、26寸6. 如图,三角形与⊙O叠合得到三条相等的弦AB、CD、EF,则以下结论正确的是( )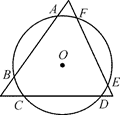 A、2∠AOB=∠AEB B、 = = C、 = = D、点O是三角形三条中线的交点7. 如图,AB是⊙O的弦,OA、OC是⊙O的半径, ,∠BAO=37°,则∠AOC的度数是( )度.
A、2∠AOB=∠AEB B、 = = C、 = = D、点O是三角形三条中线的交点7. 如图,AB是⊙O的弦,OA、OC是⊙O的半径, ,∠BAO=37°,则∠AOC的度数是( )度.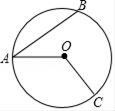 A、74 B、106 C、117 D、1278. 如图,四边形ABCD内接于⊙O,∠BOD=140°,则∠BCD等于( )
A、74 B、106 C、117 D、1278. 如图,四边形ABCD内接于⊙O,∠BOD=140°,则∠BCD等于( )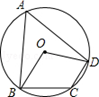 A、140° B、110° C、70° D、20°9. 如图, 中, , , , 分别为边 的中点,将 绕点 顺时针旋转 到 的位置,则整个旋转过程中线段 所扫过部分的面积(即阴影部分面积)为( )
A、140° B、110° C、70° D、20°9. 如图, 中, , , , 分别为边 的中点,将 绕点 顺时针旋转 到 的位置,则整个旋转过程中线段 所扫过部分的面积(即阴影部分面积)为( ) A、 B、 C、 D、10. 如图,AC是⊙O的直径,弦BD⊥AO于点E,连结BC,过点O作OF⊥BC于点F,若BD=8cm,AE=2cm,则OF的长度是( )
A、 B、 C、 D、10. 如图,AC是⊙O的直径,弦BD⊥AO于点E,连结BC,过点O作OF⊥BC于点F,若BD=8cm,AE=2cm,则OF的长度是( )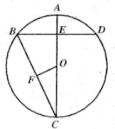 A、 cm B、 cm C、2.5cm D、3cm
A、 cm B、 cm C、2.5cm D、3cm二、填空题
-
11. 在Rt△ABC中 ,∠C=90°,AC=2 , BC=4,若以点C为圆心,AC为半径作圆,则AB边的中点E与⊙C的位置关系为 .
12. 如图,⊙O的直径为10,圆心O到弦AB的距离OM=3,则弦AB的长是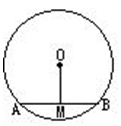 13. 如图,四边形 为 的内接四边形,若四边形 为平行四边形,则 .
13. 如图,四边形 为 的内接四边形,若四边形 为平行四边形,则 .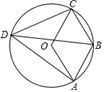 14. 如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为 .
14. 如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为 .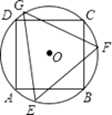 15. 某扇形的面积为 ,圆心角为120°,则该扇形的半径是 .16. 如图所示,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的半径是cm.
15. 某扇形的面积为 ,圆心角为120°,则该扇形的半径是 .16. 如图所示,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的半径是cm.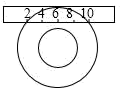
三、综合题
-
17. 如图,在Rt△ABC中,∠ACB=90°.
 (1)、以AB边上一点O为圆心作⊙O,使⊙O经过点A,C;(保留作图痕迹,不写作法)(2)、判断点B与⊙O的位置关系是.(直接写出答案)18. 如图,在⊙O中, ,CD⊥OA于D , CE⊥OB于E.求证:AD=BE.
(1)、以AB边上一点O为圆心作⊙O,使⊙O经过点A,C;(保留作图痕迹,不写作法)(2)、判断点B与⊙O的位置关系是.(直接写出答案)18. 如图,在⊙O中, ,CD⊥OA于D , CE⊥OB于E.求证:AD=BE. 19. 正方形ABCD内接于⊙O,如图所示,在劣弧 上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
19. 正方形ABCD内接于⊙O,如图所示,在劣弧 上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证: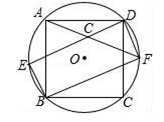 (1)、四边形EBFD是矩形;(2)、DG=BE.20. 如图,已知正△ABC,
(1)、四边形EBFD是矩形;(2)、DG=BE.20. 如图,已知正△ABC,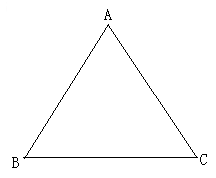 (1)、请用直尺与圆规作正△ABC的外接圆 ,并保留作图痕迹;
(1)、请用直尺与圆规作正△ABC的外接圆 ,并保留作图痕迹;
(2)、若点P是正△ABC的外接圆上的一点(不与点B,C重合),求∠BPC的度数.21. 如图,在由边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.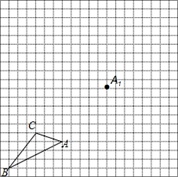 (1)、将△ABC绕点A顺时针旋转90°,画出相应的△AB1C1;(2)、将△AB1C1沿射线AA1平移到△A1B2C2处,画出△A1B2C2;(3)、点C在两次变换过程中所经过的路径长为.22. 如图,在⊙O中,半径OA⊥弦BC于点H,点D在优弧BC上
(1)、将△ABC绕点A顺时针旋转90°,画出相应的△AB1C1;(2)、将△AB1C1沿射线AA1平移到△A1B2C2处,画出△A1B2C2;(3)、点C在两次变换过程中所经过的路径长为.22. 如图,在⊙O中,半径OA⊥弦BC于点H,点D在优弧BC上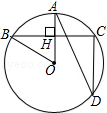 (1)、若∠AOB=50°,求∠ADC的度数;(2)、若BC=8,AH=2,求⊙O的半径.
(1)、若∠AOB=50°,求∠ADC的度数;(2)、若BC=8,AH=2,求⊙O的半径.