初中数学浙教版九年级上册3.6圆内接四边形 同步练习
试卷更新日期：2020-08-16 类型：同步测试
一、单选题
-
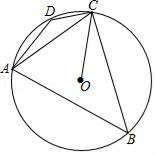
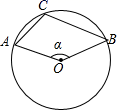
1. 如图，在⊙O中，点A、B、C在⊙O上，且∠ACB＝100°，则∠α＝（ ）
A、80° B、100° C、120° D、160°2. 如图，AB经过圆心O，四边形ABCD内接于⊙O，∠B＝3∠BAC，则∠ADC的度数为（ ）
A、100° B、112.5° C、120° D、135°3. 如图，∠AOB=100°，点C在⊙O上，且点C不与A，B重合，则∠ACB的度数为（ ）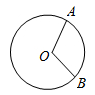
A、50° B、80°或50° C、130° D、50°或130°4. 如图，在⊙O中，弦AB垂直平分半径OC，垂足为D．若点P是⊙O上异于点A，B的任意一点，则∠APB=（ ）
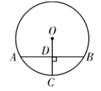A、30°或60° B、60°或150° C、30°或150° D、60°或120°5. 如图， 是圆内接四边形 的一条对角线，点 关于 的对称点 在边 上，连接 .若 ，则 的度数为（ ）
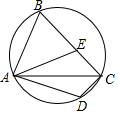A、106° B、116° C、126° D、136°6. 在圆内接四边形ABCD中， 与 的比为3：2，则∠B的度数为（ ）A、36° B、72° C、108° D、216°7. 如图，在Rt△ABC中，∠ACB=90°，以AB为直径作半圆。点D在弧 上（不与A，C重合），点E在AB上，且点D.E关于AC对称. 给出下列结论：①若∠ACE=20°，则∠BAC=25°②若BC=3，AC=4，则 给出下列判断，正确的是（ ）
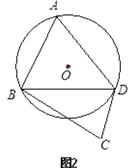
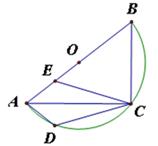A、①②都对 B、①②都错 C、①对②错 D、①错②对8. 如图所示A、B、C、D四点在⊙O上的位置，其中 =180°，且 = ， = ．若阿超在 上取一点P，在 上取一点Q，使得∠APQ=130°，则下列叙述何者正确（ ）
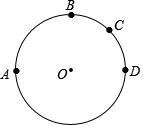A、Q点在 上，且 > B、Q点在 上，且 < C、Q点在 上，且 > D、Q点在 上，且 <9. 已知：正方形ABCD内接于⊙O ， 点P是⊙O上不同于点B、C的任意一点，则∠BPC的度数是（ ）．A、45° B、90° C、135° D、45°或135°10. 如图，四边 内接于 ，若 ，则 的度数为（ ）
A、 B、 C、 D、二、填空题
-
11. 在⊙O中，若一条弦AB的长等于这个圆的半径，则这条弦AB所对的圆周角是（注意：有两种情况，可不要少填哟！）12. 如图，四边形 内接于圆 ， 为边 延长线上一点，已知弧 的度数为 ，则 ．
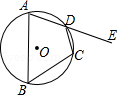13. 一条弦把圆分成1：2两部分，那么这条弦所对的圆周角的度数为.14. 如图，四边形ABCD内接于⊙O，OC∥AD，∠DAB＝60°，∠ADC＝106°，则∠OCB＝°.
15. 如图，四边形ABCD内接于⊙O ， AE⊥CB交CB的延长线于点E ， 若BA平分∠DBE ， AD＝5，CE＝ ，则AE＝ ．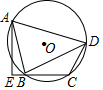
三、解答题
-
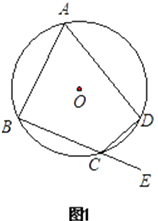
16. 如图，⊙ 的内接四边形ABCD两组对边的延长线分别相交于点E、F。
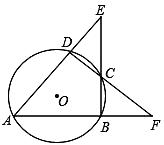(1)、若∠E=∠F时，求证：∠ADC=∠ABC；(2)、若∠E=∠F=42°时，求∠A的度数；(3)、若∠E=α，∠F=β，且。α≠β.请你用含有α、β的代数式表示∠A的大小.
