初中数学浙教版九年级上册3.5圆周角 同步练习
试卷更新日期:2020-08-16 类型:同步测试
一、单选题
-
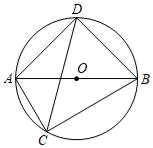
1. 如图,AB是⊙O的直径,点C在⊙O上,CD平分∠ACB交⊙O于点D , 若∠ABC=30°,则∠CAD的度数为( )
 A、100° B、105° C、110° D、1202. 如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是 上的点,若∠BOC=40°,则∠D的度数为( )
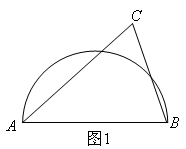
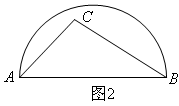
A、100° B、105° C、110° D、1202. 如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是 上的点,若∠BOC=40°,则∠D的度数为( )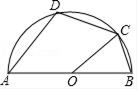 A、100° B、110° C、120° D、130°3. 用直角三角板检查半圆形的工件,下列工件合格的是( )A、
A、100° B、110° C、120° D、130°3. 用直角三角板检查半圆形的工件,下列工件合格的是( )A、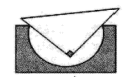 B、
B、 C、
C、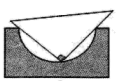 D、
D、 4. 已知A,B,C在⊙O上,△ABO为正三角形,则 ( )A、150° B、120° C、150°或 30° D、120°或 60°5. 如图,将三角板的直角顶点放在⊙O的圆心上,两条直角边分别交⊙O于A、B两点,点P在优弧AB上,且与点A、B不重合,连结PA、PB.则∠APB的大小为度.
4. 已知A,B,C在⊙O上,△ABO为正三角形,则 ( )A、150° B、120° C、150°或 30° D、120°或 60°5. 如图,将三角板的直角顶点放在⊙O的圆心上,两条直角边分别交⊙O于A、B两点,点P在优弧AB上,且与点A、B不重合,连结PA、PB.则∠APB的大小为度. 6. 如图,点A,B,C,D,E均在⊙O上,∠BAC=15°,∠CED=30°,则∠BOD的度数为( )
6. 如图,点A,B,C,D,E均在⊙O上,∠BAC=15°,∠CED=30°,则∠BOD的度数为( )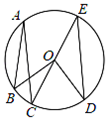 A、45° B、60° C、75° D、90°7. AB是⊙O的弦,∠AOB=80°,则弦AB所对的圆周角是( )A、40° B、140°或40° C、20° D、20°或160°8. 如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E,设∠AED=α,∠AOD=β,则( )
A、45° B、60° C、75° D、90°7. AB是⊙O的弦,∠AOB=80°,则弦AB所对的圆周角是( )A、40° B、140°或40° C、20° D、20°或160°8. 如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E,设∠AED=α,∠AOD=β,则( )
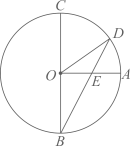 A、3α+β=180° B、2α+β=180° C、3α-β=90° D、2α-β=90°9. 数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是( )
A、3α+β=180° B、2α+β=180° C、3α-β=90° D、2α-β=90°9. 数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是( )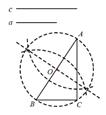 A、勾股定理 B、勾股定理的逆定理 C、直径所对的圆周角是直角 D、90°的圆周角所对的弦是直径10. 如图,已知EF是⊙O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与⊙O交于点P , 点B与点O重合,且AC大于OE , 将三角板ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x , 则x的取值范围是( )
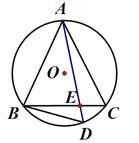
A、勾股定理 B、勾股定理的逆定理 C、直径所对的圆周角是直角 D、90°的圆周角所对的弦是直径10. 如图,已知EF是⊙O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与⊙O交于点P , 点B与点O重合,且AC大于OE , 将三角板ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x , 则x的取值范围是( )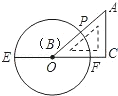 A、30≤x≤60 B、30≤x≤90 C、30≤x≤120 D、60≤x≤12011. 如图,点A,B,D,C是⊙O上的四个点,连结AB,CD并延长,相交于点E,若∠BOD=20°, ∠AOC=90°,则∠E的度数为( )
A、30≤x≤60 B、30≤x≤90 C、30≤x≤120 D、60≤x≤12011. 如图,点A,B,D,C是⊙O上的四个点,连结AB,CD并延长,相交于点E,若∠BOD=20°, ∠AOC=90°,则∠E的度数为( )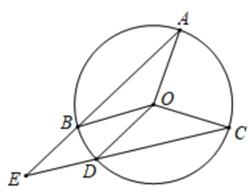 A、30° B、35° C、45° D、55°12. 如图,AB是⊙O的直径,点C,D在直径AB一侧的圆上(异于A,B两点),点E在直径AB另一侧的圆上,若∠E=42°,∠A=60°,则∠B=( )
A、30° B、35° C、45° D、55°12. 如图,AB是⊙O的直径,点C,D在直径AB一侧的圆上(异于A,B两点),点E在直径AB另一侧的圆上,若∠E=42°,∠A=60°,则∠B=( )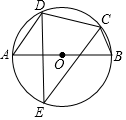 A、62° B、70° C、72° D、74°
A、62° B、70° C、72° D、74°二、填空题
-
13. 如图,量角器上 、 两点所表示的读数分别是 、 ,则 的度数为.
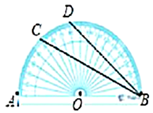 14. 如图,⊙O1的半径是⊙O2的直径,⊙O1的半径O1C交⊙O2于B,若 的度数是48°,那么 的度数是.
14. 如图,⊙O1的半径是⊙O2的直径,⊙O1的半径O1C交⊙O2于B,若 的度数是48°,那么 的度数是.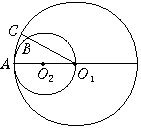 15. 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器零刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒4度的速度旋转,CP与量角器的半圆弧交于点E,第18秒时,点E在量角器上对应的读数是度.
15. 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器零刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒4度的速度旋转,CP与量角器的半圆弧交于点E,第18秒时,点E在量角器上对应的读数是度. 16. 若点O是△ABC的外心,且∠BOC=70°,则∠BAC的度数为.17. 如图,AB是半圆O的直径,弦AC=4,∠CAB=60°,点D是弧BC上的一个动点,作CG⊥AD,连结BG,在点D移动的过程中,BG的最小值是.
16. 若点O是△ABC的外心,且∠BOC=70°,则∠BAC的度数为.17. 如图,AB是半圆O的直径,弦AC=4,∠CAB=60°,点D是弧BC上的一个动点,作CG⊥AD,连结BG,在点D移动的过程中,BG的最小值是.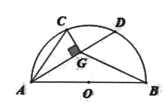
三、解答题
-
18. 如图,AB是⊙O的直径,半径OC⊥AB,过OC的中点D作弦EF∥AB,求∠ABE的度数.
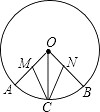
 19. 如图,已知OA、OB、OC是⊙O的三条半径,点C是弧AB的中点,M、N分别是OA、OB的中点.求证:MC=NC.
19. 如图,已知OA、OB、OC是⊙O的三条半径,点C是弧AB的中点,M、N分别是OA、OB的中点.求证:MC=NC.