初中数学浙教版八年级上册第5章 一次函数 单元检测(提高篇)
试卷更新日期:2020-08-15 类型:单元试卷
一、单选题
-
1. 声音在空气中传播的速度与气温的关系如下表:
气温T/℃
-20
-10
0
10
20
30
声速v/(m/s)
318
324
330
336
342
348
根据表格下列分析错误的是( )
A、在这个变化过程中,气温和声速都是变量 B、声速随气温的升高而增大 C、声速v与气温T的关系式为v=T+330 D、气温每升高10℃,声速增加6m/s2. 在平面直角坐标系中,已知点M(2,3),N(﹣1,﹣3),P(1,2),Q(﹣2,3),其中不可能与点A(2,﹣3)在同一函数图象上的一个点是( )A、点M B、点N C、点P D、点Q3. 一次函数y=kx+b的图像与x轴和y轴的正半轴分别交于A,B两点.已知OA+OB=6(O为坐标原点),且 =4,则这个一次函数的解析式为 ( )A、y=- x+2 B、y=-2x+4 C、y= x+2 D、y=- x+2或y=-2x+44. 已知一次函数的图象过点(0,3),且与两坐标轴在第一象限所围成的三角形面积为3,则这个一次函数的表达式为( )A、y=1.5x+3 B、y=1.5x-3 C、y=-1.5x+3 D、y=-1.5x-35. 如图,在平面直角坐标系中,A(0,1),B(3,2),点C是x上任意一点,当CA+CB有最小值时,C点的坐标为( ) A、(0,0) B、(1,0) C、(-1,0) D、(3,0)6. 小明从家出发,沿一条直道跑步,经过一段时间原路返回,刚好在第16分钟回到家中. 设小明出发第 分钟的速度为 米/分,离家的距离为 米. 与 之间的部分图象、 与 之间的部分图象分别如图1与图2(图象没画完整,其中图中的空心圈表示不包含这一点),则当小明离家600米时,所用的时间是( )分钟.
A、(0,0) B、(1,0) C、(-1,0) D、(3,0)6. 小明从家出发,沿一条直道跑步,经过一段时间原路返回,刚好在第16分钟回到家中. 设小明出发第 分钟的速度为 米/分,离家的距离为 米. 与 之间的部分图象、 与 之间的部分图象分别如图1与图2(图象没画完整,其中图中的空心圈表示不包含这一点),则当小明离家600米时,所用的时间是( )分钟. A、4.5 B、8.25 C、4.5 或8.25 D、4.5 或 8.57.
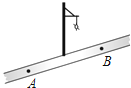
A、4.5 B、8.25 C、4.5 或8.25 D、4.5 或 8.57.如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程S之间的变化关系用图象刻画出来,大致图象是( )
 A、
A、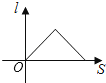
B、
B、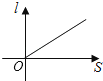
C、
C、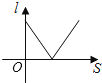
D、
D、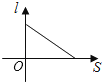 8. 甲、乙两位同学住在同一小区,学校与小区相距2700米,一天甲从小区步行出发去学校,12分钟后乙也出发,乙先骑公交自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校。已知步行速度甲比乙每分钟快5米,图中的折线表示甲、乙两人之间的距离y(米)与甲步行时间x(分钟)的函数关系图像,则( )
8. 甲、乙两位同学住在同一小区,学校与小区相距2700米,一天甲从小区步行出发去学校,12分钟后乙也出发,乙先骑公交自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校。已知步行速度甲比乙每分钟快5米,图中的折线表示甲、乙两人之间的距离y(米)与甲步行时间x(分钟)的函数关系图像,则( ) A、乙骑自行车的速度是180米/分 B、乙到还车点时,甲、乙两人相聚850米 C、自行车还车点距离学校300米 D、乙到学校时,甲距离学校200米9. 在平面直角坐标系xOy中,已知直线l1:y=kx﹣2与x轴交于点A,直线l2:
A、乙骑自行车的速度是180米/分 B、乙到还车点时,甲、乙两人相聚850米 C、自行车还车点距离学校300米 D、乙到学校时,甲距离学校200米9. 在平面直角坐标系xOy中,已知直线l1:y=kx﹣2与x轴交于点A,直线l2:y=(k﹣3)x﹣2分别与l1交于点G,与x轴交于点B.若S△GAB<S△GOA , 则下列范围中,含有符合条件的k的是( )
A、0<k<1 B、1<k<2 C、2<k<3 D、k>310. 如图,在平面直角坐标系中,点A1 , A2 , A3在直线y= x+b上,点B1 , B2 , B3在x轴上,△OA1B1 , △B1A2B2 , △B2A3B3都是等腰直角三角形,若已知点A1(1,1),则点A3的纵坐标是( )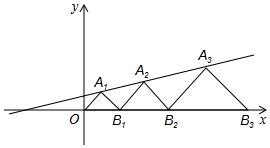 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 函数 的自变量的取值范围是.12. 如果直线 与两坐标轴所围成的面积是9,则k的值为。13. 如图,直线 与 轴, 轴分别交于点 和 , 是 上的一点,若将 沿 折叠,点 恰好落在 轴上的点 处,则直线 的解析式为.
 14. 如图所示的图像反映的过程是:甲乙两人同时从 地出发,以各自的速度匀速向 地行驶,甲先到 地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为 , 表示甲乙两人相距的距离, 表示乙行驶的时间.现有以下 个结论:① 、 两地相距 ;②点 的坐标为 ;③甲去时的速度为 ;④甲返回的速度是 .以上 个结论中正确的是.
14. 如图所示的图像反映的过程是:甲乙两人同时从 地出发,以各自的速度匀速向 地行驶,甲先到 地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为 , 表示甲乙两人相距的距离, 表示乙行驶的时间.现有以下 个结论:① 、 两地相距 ;②点 的坐标为 ;③甲去时的速度为 ;④甲返回的速度是 .以上 个结论中正确的是. 15. 如图,已知a,b,c分别是Rt△ABC的三条边长,∠C=90°,我们把关于x的形如y= 的一次函数称为“勾股一次函数”,若点P(1, )在“勾股一次函数”的图象上,且Rt△ABC的面积是5,则c的值是 .
15. 如图,已知a,b,c分别是Rt△ABC的三条边长,∠C=90°,我们把关于x的形如y= 的一次函数称为“勾股一次函数”,若点P(1, )在“勾股一次函数”的图象上,且Rt△ABC的面积是5,则c的值是 . 16. 如图,将一块等腰直角三角板ABC放置在平面直角坐标系中,∠ACB=90°,AC=BC,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限,AC所在直线的函数表达式是y=2x+4,若保持AC的长不变,当点A在y轴的正半轴滑动,点C随之在x轴的负半轴上滑动,则在滑动过程中,点B与原点O的最大距离是。
16. 如图,将一块等腰直角三角板ABC放置在平面直角坐标系中,∠ACB=90°,AC=BC,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限,AC所在直线的函数表达式是y=2x+4,若保持AC的长不变,当点A在y轴的正半轴滑动,点C随之在x轴的负半轴上滑动,则在滑动过程中,点B与原点O的最大距离是。
三、解答题
-
17. 若一次函数y=kx+b的自变量x的取值范围是-2≤x≤6,相应的函数值的范围是-11≤y≤9,求此函数的表达式.18. 如图①,平面直角坐标系中,O为原点,点A坐标为(﹣4,0),AB∥y轴,点C在y轴上,一次函数y= x+3的图象经过点B、C.
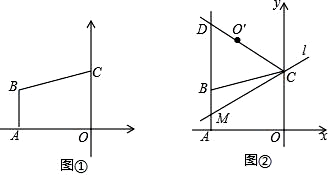 (1)、点C的坐标为 , 点B的坐标为;(2)、如图②,直线l经过点C,且与直线AB交于点M,O'与O关于直线l对称,连接CO'并延长,交射线AB于点D.
(1)、点C的坐标为 , 点B的坐标为;(2)、如图②,直线l经过点C,且与直线AB交于点M,O'与O关于直线l对称,连接CO'并延长,交射线AB于点D.①求证:△CMD是等腰三角形;
②当CD=5时,求直线l的函数表达式.
19. 已知直线y=kx+3(1-k)(其中k为常数,k≠0),k取不同数值时,可得不同直线,请探究这些直线的共同特征.
实践操作
(1)、当k=1时,直线l1的解析式为 , 请在图1中画出图象;当k=2时,直线l2的解析式为 , 请在图2中画出图象;(2)、探索发现直线y=kx+3(1-k)必经过点( , );
(3)、类比迁移矩形ABCD如图2所示,若直线y=kx+k-2(k≠0)分矩形ABCD的面积为相等的两部分,请在图中直接画出这条直线.
20. 已知一次函数y=kx+b的图象经过点A(-1,-1)和点B(1,-3)。求: (1)、求一次函数的表达式;(2)、求直线AB与坐标轴围成的三角形的面积;(3)、请在x轴上找到一点P,使得PA+PB最小,并求出P的坐标。21. 如图,直线y=-x+1和直线y=x-2相交于点P,分别与y轴交于A、B两点.
(1)、求一次函数的表达式;(2)、求直线AB与坐标轴围成的三角形的面积;(3)、请在x轴上找到一点P,使得PA+PB最小,并求出P的坐标。21. 如图,直线y=-x+1和直线y=x-2相交于点P,分别与y轴交于A、B两点.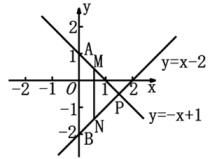 (1)、求点P的坐标;(2)、求△ABP的面积;(3)、M、N分别是直线y=-x+1和y=x-2上的两个动点,且MN∥y轴,若MN=5,直接写出M、N两点的坐标.22. 如图,在平面直角坐标系中,已知点A的坐标为(15,0),点B的坐标为(6,12),点C的坐标为(0,6),直线AB交y轴于点D,动点P从点C出发沿着y轴正方向以每秒2个单位的速度运动,同时,动点Q从点A出发沿着射线AB以每秒a个单位的速度运动,设运动时间为t秒。
(1)、求点P的坐标;(2)、求△ABP的面积;(3)、M、N分别是直线y=-x+1和y=x-2上的两个动点,且MN∥y轴,若MN=5,直接写出M、N两点的坐标.22. 如图,在平面直角坐标系中,已知点A的坐标为(15,0),点B的坐标为(6,12),点C的坐标为(0,6),直线AB交y轴于点D,动点P从点C出发沿着y轴正方向以每秒2个单位的速度运动,同时,动点Q从点A出发沿着射线AB以每秒a个单位的速度运动,设运动时间为t秒。 (1)、求直线AB的解析式和CD的长。(2)、当△PQD与△BDC全等时,求a的值。(3)、记点P关于直线BC的对称点为P',连结QP',当t=3,QP'∥BC时,求点Q的坐标。
(1)、求直线AB的解析式和CD的长。(2)、当△PQD与△BDC全等时,求a的值。(3)、记点P关于直线BC的对称点为P',连结QP',当t=3,QP'∥BC时,求点Q的坐标。