初中数学浙教版八年级上册5.5一次函数的简单应用 同步练习
试卷更新日期:2020-08-15 类型:同步测试
一、单选题
-
1. 从A地向B地打长途电话,按时收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若通话t分钟(t⩾3),则需付电话费y(元)与t(分钟)之间的函数关系式是( )
A、y=t−0.5 B、y=t−0.6 C、y=3.4t−7.8 D、y=3.4t−82. 已知汽车油箱内有油40L,每行驶100km耗油10L,则汽车行驶过程中油箱内剩余的油量Q (L)与行驶路程s(km)之间的函数表达式是( )A、Q=40+ B、Q=40﹣ C、Q=40﹣ D、Q=40+3. 公式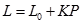 表示当重力为P时的物体作用在弹簧上时弹簧的长度.
表示当重力为P时的物体作用在弹簧上时弹簧的长度. 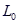 表示弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是( ) A、L=10+0.5P B、L=10+5P C、L=80+0.5P D、L=80+5P4. 汽车以60千米/时的速度在公路上匀速行驶,1小时后进入高速公路,继续以100千米/时的速度匀速行驶,则下列图象中能近似地刻画汽车行驶路程y(千米)与时间x(时)之间关系的是( )A、
表示弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是( ) A、L=10+0.5P B、L=10+5P C、L=80+0.5P D、L=80+5P4. 汽车以60千米/时的速度在公路上匀速行驶,1小时后进入高速公路,继续以100千米/时的速度匀速行驶,则下列图象中能近似地刻画汽车行驶路程y(千米)与时间x(时)之间关系的是( )A、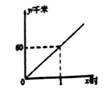 B、
B、 C、
C、 D、
D、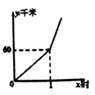 5. 甲、乙两人分别从 , 两地相向而行,他们距 地的距离 与时间 的关系如图所示,下列说法错误的是( )
5. 甲、乙两人分别从 , 两地相向而行,他们距 地的距离 与时间 的关系如图所示,下列说法错误的是( ) A、甲的速度是 B、甲出发4.5小时后与乙相遇 C、乙比甲晚出发2小时 D、乙的速度是6. 使用喷壶在家中喷洒消毒液是预防新冠病毒的有效措施.某同学为了更加合理、科学、 节约的喷洒消毒液,做了如下的记录.壶中可装消毒液 400mL,喷壶每次放出 20mL 的水,壶里的剩余消毒液量 y(mL)与喷洒次数 n(次)有如下关系:
A、甲的速度是 B、甲出发4.5小时后与乙相遇 C、乙比甲晚出发2小时 D、乙的速度是6. 使用喷壶在家中喷洒消毒液是预防新冠病毒的有效措施.某同学为了更加合理、科学、 节约的喷洒消毒液,做了如下的记录.壶中可装消毒液 400mL,喷壶每次放出 20mL 的水,壶里的剩余消毒液量 y(mL)与喷洒次数 n(次)有如下关系:喷洒次数(n)
1
2
3
4
…
壶中剩余消毒液量(mL)
380
360
340
320
…
下列结论中正确的是( )
A、y 随 n 的增加而增大 B、喷洒 10 次后,壶中剩余消毒液量为 0mL C、y 与 n 之间的关系式为 y=400﹣n D、喷洒 18 次后,壶中剩余消毒液量为 40mL7. 已知A,B两地相距12km,甲、乙两人沿同一条公路分别从A,B两地出发相向而行,甲、乙两人离B地的路程s(km)与时间t(h)的函数关系图象如图所示,则两人在甲出发后相遇所需的时间是( )
A、1.2h B、1.5h C、1.6h D、1.8h8. 某天,小明走路去学校,开始他以较慢的速度匀速前进,然后他越走越快走了一段时间,最后他以较快的速度匀速前进达到学校.小明走路的速度v(米/分钟)是时间t(分钟)的函数,能符合题意反映这一函数关系的大致图像是( )A、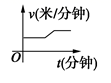 B、
B、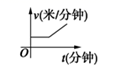 C、
C、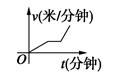 D、
D、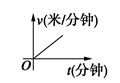 9. “龟兔首次赛跑”之后,输了比赛的兔子总结惨痛教训后.决定和乌龟再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事( 表示乌龟从起点出发所行的时间, 表示乌龟所行的路程, 表示兔子所行的路程.下列说法中:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处上了乌龟.正确的有( )
9. “龟兔首次赛跑”之后,输了比赛的兔子总结惨痛教训后.决定和乌龟再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事( 表示乌龟从起点出发所行的时间, 表示乌龟所行的路程, 表示兔子所行的路程.下列说法中:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处上了乌龟.正确的有( )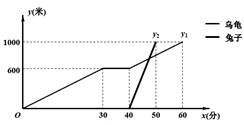 A、1个 B、2个 C、3个 D、4个10. 体育课上,20人一组进行足球比赛,每人射点球5次,已知某一组的进球总数为49个,进球情况记录如下表,其中进2个球的有x人,进3个球的有y人,若(x, y)恰好是两条直线的交点坐标,则这两条直线的解析式是( )
A、1个 B、2个 C、3个 D、4个10. 体育课上,20人一组进行足球比赛,每人射点球5次,已知某一组的进球总数为49个,进球情况记录如下表,其中进2个球的有x人,进3个球的有y人,若(x, y)恰好是两条直线的交点坐标,则这两条直线的解析式是( ) A、y=x+9与 B、y=-x+9与 C、y=-x+9与 D、y=x+9与
A、y=x+9与 B、y=-x+9与 C、y=-x+9与 D、y=x+9与二、填空题
-
11. 一辆经营长途运输的货车在高速公路的A处加满油后,以每小时80千米的速度匀速行驶,前往B地,如表记录的是货车一次加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x/时
0
1
2
2.5
余油量y/升
100
80
60
50
则y与x的函数关系式为 , 自变量x的取值范围为 .
12. 小华向果农买西红柿,连同竹篮称得总质量为3千克,需付西红柿的钱10元,若再加买0.5千克的西红柿,需多付2元,则空竹篮的质量为千克。13. 小明早上步行去车站,然后坐车去学校.下列图象中,能近似的刻画小明离学校的距离随时间变化关系的图象是 . (填序号) 14. 某商场利用“五一”开展促销活动:一次性购买某品牌服装3件,每件仅售80元,如果超过3件,则超出部分可享受8折优惠,顾客所付款y(元)与所购服装x(x≥3)件之间的函数解析式为 。15. 从A地向B地打长途电话,按时收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若通话t分钟(t≥3),则需付电话费y(元)与t(分钟)之间的函数关系式是。16. 某商店卖水果,数量x(千克)与售价y(元)之间的关系如下表,(y是x的次函数):
14. 某商场利用“五一”开展促销活动:一次性购买某品牌服装3件,每件仅售80元,如果超过3件,则超出部分可享受8折优惠,顾客所付款y(元)与所购服装x(x≥3)件之间的函数解析式为 。15. 从A地向B地打长途电话,按时收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若通话t分钟(t≥3),则需付电话费y(元)与t(分钟)之间的函数关系式是。16. 某商店卖水果,数量x(千克)与售价y(元)之间的关系如下表,(y是x的次函数):x/千克
0.5
1
1.5
2
…
y/元
1.6+0.1
3.2+0.1
4.8+0.1
6.4+0.1
当x=7千克时,售价y=元。
三、解答题
-
17. 某厂家在甲、乙两家商场销售同一种商品所获得的利润分别为y甲 , y乙(单位:元),y甲 , y乙与销售数量x(单位:件)的函数关系如图所示,请根据图象分别求出y甲 , y乙关于x的函数解析式.
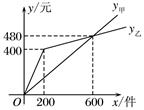 18. 学校准备添置一批计算机.
18. 学校准备添置一批计算机.方案1:到商家直接购买,每台需要7000元;
方案2:学校买零部件组装,每台需要6000元,另外需要支付安装工工资等其它费用合计3000元.设学校需要计算机x台,方案1与方案2的费用分别为 、 元.
(1)、分别写出 、 的函数关系式;(2)、当学校添置多少台计算机时,两种方案的费用相同?(3)、采用哪一种方案较省钱?说说你的理由.19. 小华是花店的一名花艺师,她每天都要为花店制作普通花束和精致花束,她每月工作20天,每天工作8小时,她的工资由基本工资和提成工资两部分构成,每月的基本工资为l800元,另每制作一束普通花束可提2元,每制作一束精致花束可提5元.她制作两种花束的数量与所用时间的关系见下表:制作普通花束(束)
制作精致花束(束)
所用时间(分钟)
10
25
600
15
30
750
请根据以上信息,解答下列问题:
(1)、小华每制作一束普通花束和每制作一束精致花束分别需要多少分钟?(2)、2019年11月花店老板要求小华本月制作普通花束的总时间X不少于3000分钟且不超过5000分钟,则小华该月收入W最多是多少元?此时小华本月制作普通花束和制作精致花束分别是多少束?20. 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动.快车离乙地的路程 与行驶的时间 之间的函数关系,如图中线段AB所示.慢车离乙地的路程 与行驶的时间 之间的函数关系,如图中线段OC所示.根据图象进行以下研究.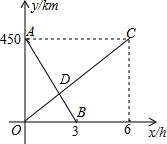 (1)、快车的速度是 ,慢车的速度是 ;(2)、求AB与OC的函数关系式.(3)、何时快车离乙地的距离大于慢车离乙地的距离?21. 有一科技小组进行机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上.甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走.如图是甲、乙两机器人之间的距离y(米)与它们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
(1)、快车的速度是 ,慢车的速度是 ;(2)、求AB与OC的函数关系式.(3)、何时快车离乙地的距离大于慢车离乙地的距离?21. 有一科技小组进行机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上.甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走.如图是甲、乙两机器人之间的距离y(米)与它们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题: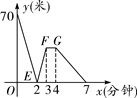 (1)、A、B两点之间的距离是米,甲机器人前2分钟的速度为米/分;(2)、若前3分钟甲机器人的速度不变,求线段EF所在直线的函数解析式;(3)、若线段 轴,则此段时间,甲机器人的速度为米/分;(4)、求A、C两点之间的距离;(5)、直接写出两机器人出发多长时间相距28米.
(1)、A、B两点之间的距离是米,甲机器人前2分钟的速度为米/分;(2)、若前3分钟甲机器人的速度不变,求线段EF所在直线的函数解析式;(3)、若线段 轴,则此段时间,甲机器人的速度为米/分;(4)、求A、C两点之间的距离;(5)、直接写出两机器人出发多长时间相距28米.