初中数学浙教版八年级上册5.4 一次函数的图象(2)同步练习
试卷更新日期:2020-08-15 类型:同步测试
一、单选题
-
1. 已知正比例函数 ,且 随 的增大而增大,则一次函数 的图象是( )A、
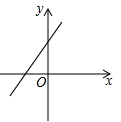 B、
B、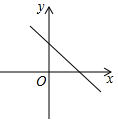 C、
C、 D、
D、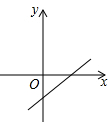 2. 如图,一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0,n>0)的图象是( )A、
2. 如图,一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0,n>0)的图象是( )A、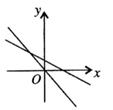 B、
B、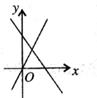 C、
C、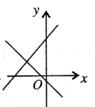 D、
D、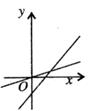 3. 若直线y=kx+b经过第一、二、四象限,则k,b的取值范围是( )A、k>0, b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<04. 下列函数中,y随着 x的减小而增大的是( )A、
3. 若直线y=kx+b经过第一、二、四象限,则k,b的取值范围是( )A、k>0, b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<04. 下列函数中,y随着 x的减小而增大的是( )A、 B、
B、 C、
C、 D、
D、 5. 一次函数y=kx+2经过点(1,1),那么这个一次函数( )A、y随x的增大而增大 B、y随x的增大而减小 C、图象经过原点 D、图象不经过第二象限6. 若一次函数 的图象经过第一、二、四象限,则下列不等式中总成立的是( )A、 >0 B、 >0 C、 >0 D、 >07. 点P(x, y )在第一象限内,且 x+y =6,点 A (4,0).设 的面积为 S ,则下列图像中,能正确反映 S 与之间的函数关系式的图像是( )A、
5. 一次函数y=kx+2经过点(1,1),那么这个一次函数( )A、y随x的增大而增大 B、y随x的增大而减小 C、图象经过原点 D、图象不经过第二象限6. 若一次函数 的图象经过第一、二、四象限,则下列不等式中总成立的是( )A、 >0 B、 >0 C、 >0 D、 >07. 点P(x, y )在第一象限内,且 x+y =6,点 A (4,0).设 的面积为 S ,则下列图像中,能正确反映 S 与之间的函数关系式的图像是( )A、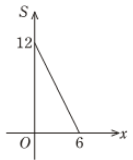 B、
B、 C、
C、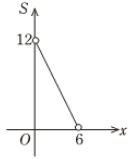 D、
D、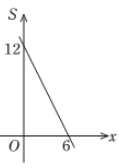 8. 一次函数 的图象经过的象限是( )A、 一、二、三 B、 二、三、四 C、一、二、四 D、一、三、四9. 关于函数y=-x+1的图象与性质,下列说法错误的是( )A、图象不经过第三象限 B、图象是与y=-x-1平行的一条直线 C、y随x的增大而减小 D、当-2≤x≤1时,函数值y有最小值310. 如图,一次函数y=kx+b的图象经过(2,0)和(0,4)两点,则下列说法正确的是( )
8. 一次函数 的图象经过的象限是( )A、 一、二、三 B、 二、三、四 C、一、二、四 D、一、三、四9. 关于函数y=-x+1的图象与性质,下列说法错误的是( )A、图象不经过第三象限 B、图象是与y=-x-1平行的一条直线 C、y随x的增大而减小 D、当-2≤x≤1时,函数值y有最小值310. 如图,一次函数y=kx+b的图象经过(2,0)和(0,4)两点,则下列说法正确的是( )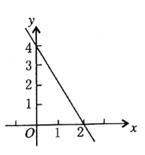 A、y随x的增大而增大 B、当x<2时,y<4 C、k=-2 D、点(5,-5)在直线y=kx+b上11. 已知一次函数y=kx+b(k,b是常数,且k≠0),x与y的部分对应值如下表所示,那么不等式kx+b<0的解集是( )
A、y随x的增大而增大 B、当x<2时,y<4 C、k=-2 D、点(5,-5)在直线y=kx+b上11. 已知一次函数y=kx+b(k,b是常数,且k≠0),x与y的部分对应值如下表所示,那么不等式kx+b<0的解集是( )x
-2
-1
0
1
2
3
y
3
2
1
0
-1
-2
A、x<0 B、x>0 C、x<1 D、x>112. 点A(x1 , y1)、B(x2 , y2)都在直线y=kx+2(k<0)上,且x1<x2 , 则y1、y2的大小关系是( )A、y1=y2 B、y1<y2 C、y1>y2 D、无法判断二、填空题
-
13. 某个函数具有性质:当x<0时,y随x的增大而减小,这个函数的表达式可以是(只要写出一个符合题意的答案即可).14. 已知直线y=(k﹣2)x+k经过第一、二、四象限,则k的取值范围是15. 若一次函数y=kx+b交于y轴的负半轴,且y的值随x的增大而减少,则k0,b0.(填“>”、“<”或“=” )16. 已知点 , 在正比例函数 的图像上,则mn.(填“>”“<”或“=”)17. 如图,正比例函数 和一次函数 的图象相交于点 .当 时, (填“>”或“<”)

三、解答题
-
18. 已知关于x的一次函数y=(3a-7)x+a-2的图象与y轴的交点在x轴的上方,且当x1<x2时,对应的函数值满足y1>y2 , 求a的取值范围.19. 已知△ABC在平面直角坐标系中的位置如图所示,将△ABC向右平移5个单位长度,再F向下平移3个单位长度得到△A1B1C1(图中每个小方格边长均为1个单位长度)
 (1)、在图中画出平移后的△A1B1C1;(2)、直接写出△A1B1C1各顶点的坐标A1 , B1 , C1 ,(3)、在x轴上找到一点M,当AM+A1M取最小值时,M点的坐标是 。20. 已知函数y=(2m+1)x+m﹣3.(1)、若函数图象经过原点,求m的值;(2)、若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;(3)、若这个函数是一次函数,且图象不经过第四象限,求m的取值范围.21. 已知函数y1=2x-4与y2=-2x+8的图象,观察图象并回答问题:
(1)、在图中画出平移后的△A1B1C1;(2)、直接写出△A1B1C1各顶点的坐标A1 , B1 , C1 ,(3)、在x轴上找到一点M,当AM+A1M取最小值时,M点的坐标是 。20. 已知函数y=(2m+1)x+m﹣3.(1)、若函数图象经过原点,求m的值;(2)、若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;(3)、若这个函数是一次函数,且图象不经过第四象限,求m的取值范围.21. 已知函数y1=2x-4与y2=-2x+8的图象,观察图象并回答问题: (1)、x取何值时,2x-4>0?(2)、x取何值时,-2x+8>0?(3)、x取何值时,2x-4>0与-2x+8>0同时成立?(4)、求函数y1=2x-4与y2=-2x+8的图象与x轴所围成的三角形的面积?22. 某服装店的一次性购进甲、乙两种童衣共100件进行销售,其中甲种童衣的进价为80元/件,售价为120元/件;乙种童衣的进价为100元/件,售价为150元/件。设购进甲种童衣的数量为 (件),销售完这批童衣的总利润为 (元)。(1)、请求出 与 之间的函数关系式(不用写出 的取值范围);(2)、如果购进的甲种童衣的件数不少于乙种童衣件数的3倍,求购进甲种童衣多少件式,这批童衣销售完利润最多?最多可以获利多少元?23. 某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
(1)、x取何值时,2x-4>0?(2)、x取何值时,-2x+8>0?(3)、x取何值时,2x-4>0与-2x+8>0同时成立?(4)、求函数y1=2x-4与y2=-2x+8的图象与x轴所围成的三角形的面积?22. 某服装店的一次性购进甲、乙两种童衣共100件进行销售,其中甲种童衣的进价为80元/件,售价为120元/件;乙种童衣的进价为100元/件,售价为150元/件。设购进甲种童衣的数量为 (件),销售完这批童衣的总利润为 (元)。(1)、请求出 与 之间的函数关系式(不用写出 的取值范围);(2)、如果购进的甲种童衣的件数不少于乙种童衣件数的3倍,求购进甲种童衣多少件式,这批童衣销售完利润最多?最多可以获利多少元?23. 某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.
 (1)、分别写出选择银卡、普通票消费时,y与x之间的函数关系式;(2)、在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;(3)、请根据函数图象,直接写出选择哪种消费方式更合算.
(1)、分别写出选择银卡、普通票消费时,y与x之间的函数关系式;(2)、在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;(3)、请根据函数图象,直接写出选择哪种消费方式更合算.