初中数学青岛版九年级上学期第2章2.2 30°,45°,60°角的三角比

试卷更新日期：2020-08-13 类型：同步测试

进入出卷网下载

一、单选题

1. 在Rt△ABC中，∠C=90^° ，则下列式子成立的是（）

A、sinA=sinB B、sinA=cosB C、tanA=tanB D、cosA=tanB

查看试题解析
2. 点（-sin60°，cos60°）关于y轴对称的点的坐标是（）

A、（ $\frac{\sqrt{3}}{2}$ ， $\frac{1}{2}$ ） B、（- $\frac{\sqrt{3}}{2}$ ， $\frac{1}{2}$ ） C、（- $\frac{\sqrt{3}}{2}$ ，- $\frac{1}{2}$ ） D、（- $\frac{1}{2}$ ，- $\frac{3}{2}$ ）

查看试题解析
3. 如果∠A是锐角，则下列结论正确个数为（　　）个．
① $\sqrt{(\sin A - 1)^{2}}$ =sinA-1；②sinA+cosA＞1；③tanA＞sinA；④cosA=sin（90°﹣∠A）

A、1 B、2 C、3 D、4

查看试题解析
4. 如果∠A为锐角，cosA= $\frac{\sqrt{3}}{3}$ ，那么∠A所在的范围是（　　）

A、0°＜∠A＜30° B、30°＜∠A＜45° C、45°＜∠A＜60° D、60°＜∠A＜90°

查看试题解析
5. 若α为锐角，且 sin(α-10°）= $\frac{\sqrt{3}}{2}$ ，则α等于（）

A、80° B、70° C、60° D、50°

查看试题解析
6. 式子2cos30°－tan45°－ $\sqrt{{(1 - \tan 60^{\circ})}^{2}}$ 的值是（）

A、2 $\sqrt{3}$ －2 B、0 C、2 $\sqrt{3}$ D、2

查看试题解析
7. △ABC中，∠A，∠B均为锐角，且（tanB﹣ $\sqrt{3}$ ）（2sinA﹣ $\sqrt{3}$ ）=0，则△ABC一定是（）

A、等腰三角形 B、等边三角形 C、直角三角形 D、有一个角是60°的三角形

查看试题解析
8. 因为cos60°= $\frac{1}{2}$ ，cos240°=﹣ $\frac{1}{2}$ ，所以cos240°=cos（180°+60°）=﹣cos60°；由此猜想、推理知：当α为锐角时有cos（180°+α）=﹣cosα，由此可知：cos210°=（）

A、﹣ $\frac{1}{2}$ B、﹣ $\frac{\sqrt{2}}{2}$ C、﹣ $\frac{\sqrt{3}}{2}$ D、﹣ $\sqrt{3}$

查看试题解析
9. 在△ABC中， ${(\sqrt{3} \tan A - 3)}^{2} + | 2 \cos B - \sqrt{3} | = 0$ ，则△ABC为（）

A、直角三角形 B、等边三角形 C、含60°的任意三角形 D、是顶角为钝角的等腰三角形

查看试题解析
10. 如图，A、B、C是小正方形的顶点，且每个小正方形的边长为l，则tan∠BAC为（）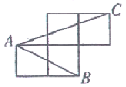

A、 $\frac{1}{2}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{3}}{3}$ D、1

查看试题解析
11. 按如图所示的运算程序，能使输出的y值为 $\frac{1}{2}$ 的是（）

A、α=60°，β=45° B、α=30°，β=45° C、α=30°，β=30° D、α=45°，β=30°

查看试题解析
12. 关于三角函数有如下公式：
sin（α+β）=sinαcosβ+cosαsinβ，sin（α﹣β）=sinαcosβ﹣cosαsinβ

cos（α+β）=cosαcosβ﹣sinαsinβ，cos（α﹣β）=cosαcosβ+sinαsinβ

tan（α+β）= $\frac{t a n α + t a n β}{1 - t a n α t a n β}$ （1﹣tanαtanβ≠0），

合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值，如sin90°=sin（30°+60°）=sin30°cos60°+cos30°sin60°= $\frac{1}{2} \times \frac{1}{2} + \frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}$ =1。

利用上述公式计算下列三角函数①sin105°= $\frac{\sqrt{6} + \sqrt{2}}{4}$ ，②tan105°=﹣2﹣ $\sqrt{3}$ ，③sin15°= $\frac{\sqrt{6} - \sqrt{2}}{4}$ ，④cos90°=0.

其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 比较大小：tan30° cos30°（用“＞”或“＜”填空）

查看试题解析
14. 已知锐角A满足4sin²A=3，则∠A=。

查看试题解析
15. 在 $R t Δ A B C$ 中, $∠ C = 90^{0}$ , $A C = 1$ , $A B = 2$ ,则 $∠ A$ =度。

查看试题解析
16. 若tan（α–15°）= $\sqrt{3}$ ，则锐角α的度数是．

查看试题解析
17. $\frac{\sin 60 °}{1 + \tan 45 °} + \tan 30 ° =$ 。

查看试题解析
18. 在△ABC中，若 $|tan A - 1 |$ + ${(\frac{\sqrt{3}}{2} - cos B)}^{2} = 0$ ，则∠C的度数为.

查看试题解析
19. 如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE ，点B的对应点D恰好落在BC边上，若AC＝ $\sqrt{3}$ ，∠B＝60°，则CD的长为．

查看试题解析
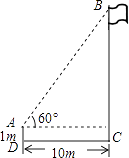
20.
如图，在一次数学课外实践活动中，小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°，测角仪高AD为1m，则旗杆高BC为 m（结果保留根号）．

查看试题解析

三、解答题

21. 计算： $\frac{2 {sin}^{2} 60 ° - cos 60 °}{{tan}^{2} 60 ° + 4 cos 45 °}$ ．

查看试题解析
22. 计算： $\tan^{2} 60 ° + 4 \cos 45 ° \cdot \sin 30 ° - {(1 - \cos 60 °)}^{- 2}$

查看试题解析
23. 计算

(1)、cos45°-2sin30°+(-2)°

(2)、2tan30°-|1- $\sqrt{3}$ |+(2017- $\sqrt{2}$ )°+ $\sqrt{\frac{1}{3}}$

查看试题解析
24. 化简：cos²1°+cos²2°+cos²3°+…+cos²89°．

查看试题解析
25.
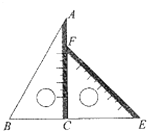
数学拓展课程《玩转学具》课堂中，小陆同学发现：一副三角板中，含45°的三角板的斜边与含30°的三角板的长直角边相等，于是，小陆同学提出一个问题：如图，将一副三角板直角顶点重合拼放在一起，点B，C，E在同一直线上，若BC=2，求AF的长．
请你运用所学的数学知识解决这个问题.

查看试题解析
26. 某海船以 $(2 \sqrt{3} + 2)$ 海里/小时的速度向北偏东70°方向行驶，在A处看见灯塔B在海船的北偏东40°方向，5小时后船行驶到C处，发现此时灯塔B在海船的北偏西65°方向，求此时灯塔B到C处的距离。

查看试题解析
27. 如图，海中有一小岛P，在距小岛16 $\sqrt{3}$ 海里范围内有暗礁，一轮船自西向东航行，它在A处测得小岛P位于北偏东45°，且A，P之间的距离为32海里，若轮船继续向正东方向航行，有无触礁的危险？请通过计算加以说明．如果有危险，轮船自A处开始至少沿东偏南多少度方向改变航向，才能安全通过这一海域？

查看试题解析

初中数学青岛版九年级上学期 第2章2.2 30°,45°,60°角的三角比

一、单选题

二、填空题

三、解答题

初中数学青岛版九年级上学期第2章2.2 30°,45°,60°角的三角比