初中数学青岛版九年级上学期 第2章 2.1锐角三角比
试卷更新日期:2020-08-13 类型:同步测试
一、单选题
-
1. Rt△ABC中,如果各边长度都扩大 倍,则锐角A的各个三角函数值( )A、不变化 B、扩大2倍 C、缩小 D、不能确定2. 如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于cosA的是( )
 A、 B、 C、 D、3. 如图,在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树的坡面上的距离AB为( )米。
A、 B、 C、 D、3. 如图,在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树的坡面上的距离AB为( )米。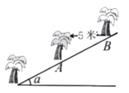 A、5cosα B、 C、5sinα D、4. 如图,某停车场入口的栏杆 ,从水平位置绕点 旋转到 的位置,已知 的长为 米.若栏杆的旋转角 ,则栏杆 端升高的高度为( )
A、5cosα B、 C、5sinα D、4. 如图,某停车场入口的栏杆 ,从水平位置绕点 旋转到 的位置,已知 的长为 米.若栏杆的旋转角 ,则栏杆 端升高的高度为( )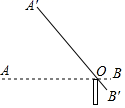 A、 米 B、 米 C、 米 D、 米5. 已知甲、乙两坡的坡角分别为α、β,若甲坡比乙坡更陡些,则下列结论正确的是( )A、tanα<tanβ B、sinα<sinβ C、cosα<cosβ D、cosα>cosβ6. 如图,在平面直角坐标系中,∠α的一边与x轴正半轴重合,顶点为坐标原点,另一边过点A(1,2),那么sinα的值为( )
A、 米 B、 米 C、 米 D、 米5. 已知甲、乙两坡的坡角分别为α、β,若甲坡比乙坡更陡些,则下列结论正确的是( )A、tanα<tanβ B、sinα<sinβ C、cosα<cosβ D、cosα>cosβ6. 如图,在平面直角坐标系中,∠α的一边与x轴正半轴重合,顶点为坐标原点,另一边过点A(1,2),那么sinα的值为( )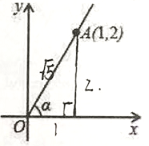 A、 B、 C、2 D、7. 如图,∠AOB是放置在正方形网格中的一个角,则tan∠AOB( )
A、 B、 C、2 D、7. 如图,∠AOB是放置在正方形网格中的一个角,则tan∠AOB( ) A、 B、 C、1 D、8. 如图,在△ABC与△A′B′C中,AB=AC=A′B′=A′C,∠B+∠B′=90°,△ABC,△A′B′C′的面积分别为S1、S2 , 则( )
A、 B、 C、1 D、8. 如图,在△ABC与△A′B′C中,AB=AC=A′B′=A′C,∠B+∠B′=90°,△ABC,△A′B′C′的面积分别为S1、S2 , 则( )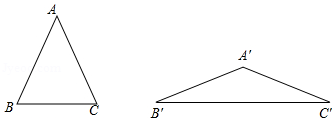 A、S1>S2 B、S1=S2 C、S1<S2 D、无法比较S1、S2的大小关系9. 如何求tan75°的值?按下列方法作图可解决问题,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BM上截取线段BD,使BD=AB,连接AD,依据此图可求得tan75°的值为( )
A、S1>S2 B、S1=S2 C、S1<S2 D、无法比较S1、S2的大小关系9. 如何求tan75°的值?按下列方法作图可解决问题,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BM上截取线段BD,使BD=AB,连接AD,依据此图可求得tan75°的值为( )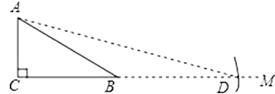 A、2 B、2+ C、1+ D、10. 如图, 在△ABC中,∠BAC=90°, AB=20, AC=15, △ABC的高AD与角平分线CF交于点E,则 的值为( )
A、2 B、2+ C、1+ D、10. 如图, 在△ABC中,∠BAC=90°, AB=20, AC=15, △ABC的高AD与角平分线CF交于点E,则 的值为( )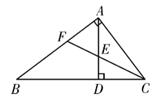 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: .12. 已知 ,且 为锐角,则m的取值范围是 .13. 在Rt△ABC中,∠C=90°,tanA= ,△ABC的周长为18,则S△ABC=.14. 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,若BC=6,AC=8,则tan∠ACD的值为 .
 15. 如图,菱形ABCD的对角线AC,BD相交于点O.若tan∠BAC= ,AC=6,则BD的长是.
15. 如图,菱形ABCD的对角线AC,BD相交于点O.若tan∠BAC= ,AC=6,则BD的长是.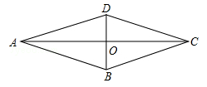 16. 如图,△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE.若BE=9,BC=12,则cosC= .
16. 如图,△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE.若BE=9,BC=12,则cosC= . 17. 为解决停车难得问题,在如图一段长56米的路段开辟停车位,每个车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出个这样的停车位( )
17. 为解决停车难得问题,在如图一段长56米的路段开辟停车位,每个车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出个这样的停车位( ) 18. 图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ,tanβ= ,以O为原点,OA所在直线为x轴建立直角坐标系,则点P到水面OA的距离是 m.
18. 图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ,tanβ= ,以O为原点,OA所在直线为x轴建立直角坐标系,则点P到水面OA的距离是 m.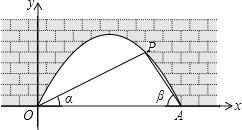
三、解答题
-
19. 在Rt△ABC中,∠C=90°,若 ,求cosA,sinB,cosB.20. 已知tanα= ,α是锐角,求tan(9O°﹣α),sinα,cosα的值.21. 如图,四边形ABCD中,∠ADB=∠DBC=90°,AD=6,CD=12,tanA= ,求sinC的值.
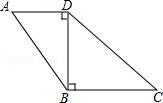 22. 在 中, , , , 的对边分别为a,b,c, , ,求c的值.23. 如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA= .
22. 在 中, , , , 的对边分别为a,b,c, , ,求c的值.23. 如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA= .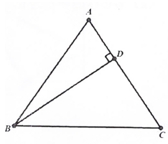 (1)、求BD的长.(2)、求tanC的值.24. 如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα= = ,根据上述角的余切定义,解下列问题:
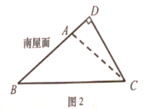
(1)、求BD的长.(2)、求tanC的值.24. 如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα= = ,根据上述角的余切定义,解下列问题: (1)、ctan30°=;(2)、如图,已知tanA= ,其中∠A为锐角,试求ctanA的值.25. 太阳能光伏建筑是太阳能光伏系统与现代绿色环保住宅的完美结合,老刘准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°.求改建后南屋面边沿增加部分AD的长,(结果精确到0.1米)
(1)、ctan30°=;(2)、如图,已知tanA= ,其中∠A为锐角,试求ctanA的值.25. 太阳能光伏建筑是太阳能光伏系统与现代绿色环保住宅的完美结合,老刘准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°.求改建后南屋面边沿增加部分AD的长,(结果精确到0.1米)(参考数据:sin18°≈031,cos18°≈0.95,tan18v≈0.32,sin36°≈0.59)

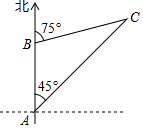
 26. 一艘货轮以34海里/时的速度在海面上向正南方向航行,当它行驶至B处时,某观察者发现在货轮的北偏东75°方向有一灯塔C;货轮继续向南航行1.5小时后到达A处,某观察者再次发现灯塔C在货轮的东北方向.求此时货轮与灯塔C的距离.(结果保留到个位)(参考数据:sin75°≈0.97,cos75°≈0.29,tan75°≈3.73,
26. 一艘货轮以34海里/时的速度在海面上向正南方向航行,当它行驶至B处时,某观察者发现在货轮的北偏东75°方向有一灯塔C;货轮继续向南航行1.5小时后到达A处,某观察者再次发现灯塔C在货轮的东北方向.求此时货轮与灯塔C的距离.(结果保留到个位)(参考数据:sin75°≈0.97,cos75°≈0.29,tan75°≈3.73,