山东省2019-2020学年高一上学期数学选课走班第二次调考试卷

试卷更新日期：2020-08-13 类型：月考试卷

进入出卷网下载

一、单选题

1. 设集合 $A = {x | 1 \leq \log_{2} x \leq 3}$ ， $B = {x | x^{2} - 3 x - 4 < 0}$ ，则 $A \cup B$ 等于（）

A、 $(- 1, 2)$ B、 $(- 1, 8]$ C、 $[2, 4)$ D、 $[4, 8]$

查看试题解析
2. 下列说法中，正确的是（）

A、任意两个单位向量都是相等的向量 B、若A，B是平面内的两个不同的点，则 $\vec{A B} = \vec{B A}$ C、若向量 $\vec{a} / / \vec{b}$ ， $\vec{b} / / \vec{c}$ ，则 $\vec{a} / / \vec{c}$ D、零向量与任意向量平行

查看试题解析
3. 已知 $B$ 是非空集合， $p$ ： $A = \emptyset$ ， $q$ ： $A \cup B = B$ ，则p是q的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 如图，网格纸上小正方形的边长为1，D，E分别是 $Δ A B C$ 的边 $A B$ ， $A C$ 的中点，则（）

A、 $| \vec{A B} | = 5$ 且 $| \vec{B C} | = 2.5 | \vec{D E} |$ B、 $| \vec{A B} | = 5$ 且 $| \vec{B C} | = 2 | \vec{D E} |$ C、 $| \vec{A B} | = 6$ 且 $| \vec{B C} | = 2 | \vec{D E} |$ D、 $| \vec{A B} | = 6$ 且 $| \vec{B C} | = 3 | \vec{D E} |$

查看试题解析
5. 某地有两个国家AAAA级旅游景区——甲景区和乙景区.相关部门统计了这两个景区2019年1月至6月的月客流量（单位：百人），得到如图所示的茎叶图.关于2019年1月至6月这两个景区的月客流量，以下结论错误的是（）

A、甲景区月客流量的中位数为12950人 B、乙景区月客流量的中位数为12450人 C、甲景区月客流量的极差为3200人 D、乙景区月客流量的极差为3100人

查看试题解析
6. 为了检验某厂生产的取暖器是否合格，先从500台取暖器中取50台进行检验，用随机数表抽取样本，将500台取暖器编号为001，002，…，500.下图提供了随机数表第7行至第9行的数据：
82 42 17 53 31    57 24 55 06 88    77 04 74 47 67    21 76 33 50 25    83 92 12 06 76

63 01 63 78 59    16 95 56 67 19    98 10 50 71 75    12 86 73 58 07    44 39 52 38 79

33 21 12 34 29    78 64 56 07 82    52 42 07 44 38    15 51 00 13 42    99 66 02 79 54

若从表中第7行第4列开始向右依次读取3个数据，则抽出第4台取暖器的编号为（    ）

A、217 B、206 C、245 D、212

查看试题解析
7. 从装有完全相同的4个红球和2个黄球的盒子中任取2个小球，则互为对立事件的是（）

A、“至少一个红球”与“至少一个黄球” B、“至多一个红球”与“都是红球” C、“都是红球”与“都是黄球” D、“至少一个红球”与“至多一个黄球”

查看试题解析
8. 甲、乙两人近五次某项测试成绩的得分情况如图所示，则（）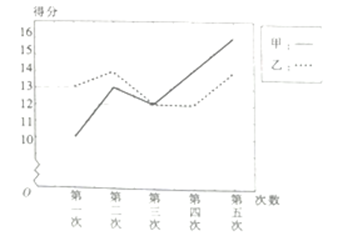

A、甲得分的平均数比乙的大 B、乙的成绩更稳定 C、甲得分的中位数比乙的大 D、甲的成绩更稳定

查看试题解析
9. 某社区组织“学习强国”的知识竞赛，从参加竞赛的市民中抽出40人，将其成绩分成以下6组：第1组 $[40 ， 50)$ ，第2组 $[50 ， 60)$ ，第3组 $[60 ， 70)$ ，第4组 $[70 ， 80)$ ，第5组 $[80 ， 90)$ ，第6组 $[90 ， 100]$ ，得到如图所示的频率分布直方图．现采用分层抽样的方法，从第2，3，4组中按分层抽样抽取8人，则第2，3，4组抽取的人数依次为（）

A、1，3，4 B、2，3，3 C、2，2，4 D、1，1，6

查看试题解析
10. 已知函数 $f (x) = - \frac{4}{3} x^{2} + a x + \frac{5}{3}$ ，若 $f (x) ⩾ 0$ 在 $[- 1 ， 1]$ 上恒成立，则a的取值范围是（）

A、 $[- \frac{1}{3} ， \frac{1}{3}]$ B、 $[- 1 ， - \frac{1}{3}]$ C、 $[- 1 ， 1]$ D、 $[- 1 ， \frac{1}{3}]$

查看试题解析

二、多选题

11. 若函数 $f (x) = {\begin{array}{l} - x^{2} + 2 a, x \leq - 1 \\ a x + 4, x > - 1 \end{array}$ 在 $R$ 上是单调函数，则a的取值可能是（）

A、0 B、1 C、 $\frac{3}{2}$ D、3

查看试题解析
12. 已知函数 $f (x - 2)$ 是定义在R上的偶函数，且对任意的 $x_{1}, x_{2} \in [0, + \infty) (x_{1} \neq x_{2})$ ，总有 $\frac{f (x_{1} - 2) - f (x_{2} - 2)}{x_{1} - x_{2}} > 0$ ，则（）

A、 $f (- 6) < f (0)$ B、 $f (0) < f (- 3)$ C、 $f (0) < f (- 6)$ D、 $f (- 3) < f (0)$

查看试题解析
13. 已知函数 $f (x) = {\begin{array}{l} x + 2 a ， x < 0 \\ x^{2} - a x ， x \geq 0 \end{array}$ ，若关于x的方程 $f (f (x)) = 0$ 有8个不同的实根，则a的值可能为（）.

A、-6 B、8 C、9 D、12

查看试题解析

三、填空题

14. 已知 $x \in (0, + \infty)$ ，则 $y = \frac{x^{2} + 3 x + 4}{x}$ 的最小值为.

查看试题解析
15. 抛掷一枚质地均匀的骰子（六个面上的点数分别为1，2，3，4，5，6），事件A为“正面朝上的点数为3”，事件B为“正面朝上的点数为偶数”，则 $P (A + B) =$ .

查看试题解析
16. 第28届金鸡百花电影节将在福建省厦门市举办，近日首批影展片单揭晓，《南方车站的聚会》《春江水暖》《第一次的离别》《春潮》《抵达之谜》五部优秀作品将在电影节进行展映．若从这五部作品中随机选择两部放在展映的前两位，则《春潮》与《抵达之谜》至少有一部被选中的概率为．

查看试题解析

四、双空题

17. 已知函数 $f (x) = - \frac{1}{4} x^{2} + 2 x + 3$ ， $g (x) = | \frac{3}{2} x - 3 |$ ，若函数 $F (x) = {\begin{array}{l} f (x) ， f (x) < g (x) \\ g (x) ， f (x) \geq g (x) \end{array}$ ，则 $F (2) =$ ， $F (x)$ 的最大值为.

查看试题解析

五、解答题

18. 已知集合 $A = {x | x \leq a - 2$ 或 $x > a + 3}$ , $B = {x | y = \log_{3} x + \log_{3} (5 - x)}$ .

(1)、当 $a = 1$ 时,求 $A \cup B$ ;

(2)、若 $A \cap B = B$ ,求实数 $a$ 的取值范围.

查看试题解析
19.

(1)、求值 $\log_{3} 4 \cdot \log_{2} 9 + \lg 20 - \frac{1}{2} \lg 4 + {0.25}^{- 0.5}$ .

(2)、已知 $a, b \in R$ ，证明： $2 (a^{2} + 4 b^{2}) \geq {(a + 2 b)}^{2}$ .

查看试题解析

20. 为了了解学生的学习情况，一次测试中，科任老师从本班中抽取了n个学生的成绩（满分100分，且抽取的学生成绩均在

[40 ， 100]

内）进行统计分析.按照

[40 ， 50)

，

[50 ， 60)

，

[60 ， 70)

，

[70 ， 80)

，

[80 ， 90)

，

[90 ， 100]

的分组作出频率分布直方图和频数分布表.

频数分布表
$[40 ， 50)$	x
$[50 ， 60)$	4
$[60 ， 70)$	10
$[70 ， 80)$	12
$[80 ， 90)$	8
$[90 ， 100]$	4

(1)、求n，a，x的值；

(2)、在选取的样本中，从低于60分的学生中随机抽取两名学生，试问这两名学生在同一组的概率是多少？

查看试题解析

21. 某校针对校食堂饭菜质量开展问卷调查，提供满意与不满意两种回答，调查结果如下表（单位：人）：

学生

高一

高二

高三

满意

500

600

800

不满意

300

200

400

(1)、求从所有参与调查的人中任选1人是高三学生的概率；

(2)、从参与调查的高三学生中，用分层抽样的方法抽取6人，在这6人中任意选取2人，求这两人对校食堂饭菜质量都满意的概率.

查看试题解析
22. 节约资源和保护环境是中国的基本国策.某化工企业,积极响应国家要求,探索改良工艺,使排放的废气中含有的污染物数量逐渐减少.已知改良工艺前所排放的废气中含有的污染物数量为 ${2mg/m}^{3}$ ,首次改良后所排放的废气中含有的污染物数量为 $1 {.94mg/m}^{3}$ .设改良工艺前所排放的废气中含有的污染物数量为 $r_{0}$ ,首次改良工艺后所排放的废气中含有的污染物数量为 $r_{1}$ ,则第n次改良后所排放的废气中的污染物数量 $r_{n}$ ,可由函数模型 $r_{n} = r_{0} - (r_{0} - r_{1}) \cdot 5^{0.5 n + p} (p \in R ， n \in N *)$ 给出,其中n是指改良工艺的次数.

(1)、试求改良后所排放的废气中含有的污染物数量的函数模型;

(2)、依据国家环保要求,企业所排放的废气中含有的污染物数量不能超过 $0 {.08mg/m}^{3}$ ,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.
（参考数据:取 $\lg 2 = 0.3$ ）

查看试题解析
23. 已知函数 $f (x) = \frac{2 e^{x} + 2 e^{- x}}{3}$ ，其中e为自然对数的底数.

(1)、证明: $f (x)$ 在 $(0, + \infty)$ 上单调递增；

(2)、函数 $g (x) = \frac{5}{3} - x^{2}$ ，如果总存在 $x_{1} \in [- a, a] (a > 0)$ ，对任意 $x_{2} \in R, f (x_{1}) ⩾ g (x_{2})$ 都成立，求实数a的取值范围.

查看试题解析

学生	高一	高二	高三
满意	500	600	800
不满意	300	200	400