上海市浦东新区第四教育署2019-2020学年九年级上学期数学10月月考试卷
试卷更新日期:2020-08-13 类型:月考试卷
一、单选题
-
1. 如果 ,那么下列各式中不成立的是( )A、 ; B、 ; C、 ; D、2. 如果延长线段AB到C,使得BC= AB,那么AC:AB等于( )A、2:1 B、2:3 C、3:1 D、3:23. 已知 ,点A、B、C对应点分别是D、E、F, ,那么 等于( )A、 B、 C、 D、4. 如图,在 中,下列所给的四个条件,其中不一定能得到 的条件是( )
 A、 B、 C、 D、5. 如图, 在边长为1个单位的方格纸中,它的顶点在小正方形顶点位置,其中点A、B、C、D也是小正方形的顶点,那么与 相似的是( )
A、 B、 C、 D、5. 如图, 在边长为1个单位的方格纸中,它的顶点在小正方形顶点位置,其中点A、B、C、D也是小正方形的顶点,那么与 相似的是( )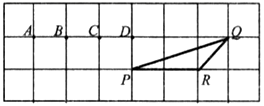 A、以点P、Q、A为顶点的三角形; B、以点P、Q、B为顶点的三角形 C、以点P、Q、C为顶点的三角形 D、以点P、Q、D为顶点的三角形6. 如图,已知在梯形 中, ∥ , ,如果对角线 与 相交于点O,△ 、△ 、△ 、△ 的面积分别记作 、 、 、 ,那么下列结论中,错误的是( )
A、以点P、Q、A为顶点的三角形; B、以点P、Q、B为顶点的三角形 C、以点P、Q、C为顶点的三角形 D、以点P、Q、D为顶点的三角形6. 如图,已知在梯形 中, ∥ , ,如果对角线 与 相交于点O,△ 、△ 、△ 、△ 的面积分别记作 、 、 、 ,那么下列结论中,错误的是( )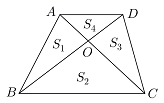 A、 ; B、 ; C、 ; D、 ;
A、 ; B、 ; C、 ; D、 ;二、填空题
-
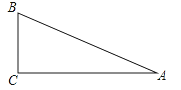
7. 已知 ,则 的值为 .8. 已知点P在线段 上, ,那么 .9. 已知线段a=4,c=9,那么a和c的比例中项b= .10. 如图,斜坡AB的坡度i=1:3,该斜坡的水平距离AC=6米,那么斜坡AB的长等于 米.
 11. 如果两个相似三角形的面积之比是9:25,其中小三角形一边上的中线长是12cm,那么大三角形对应边上的中线长是cm.12.
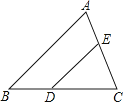
11. 如果两个相似三角形的面积之比是9:25,其中小三角形一边上的中线长是12cm,那么大三角形对应边上的中线长是cm.12.如图,已知D , E分别是△ABC的边BC和AC上的点,AE=2,CE=3,要使DE∥AB , 那么BC:CD应等于 .
 13. 已知点 是面积为 的△ 的重心,那么△ 的面积等于;14. 如图,P为平行四边形 边 上一点,E、F分别为 、 的中点,若 的面积为3,那么 与 的面积和等于.
13. 已知点 是面积为 的△ 的重心,那么△ 的面积等于;14. 如图,P为平行四边形 边 上一点,E、F分别为 、 的中点,若 的面积为3,那么 与 的面积和等于.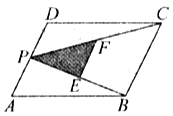 15. 已知点 是线段 上的黄金分割点, ,且 ,那么 .16. 如图,正方形 的边 在 的边 上,顶点D、G分别在 、 上, ,如果 , ,那么正方形 的边长等于.
15. 已知点 是线段 上的黄金分割点, ,且 ,那么 .16. 如图,正方形 的边 在 的边 上,顶点D、G分别在 、 上, ,如果 , ,那么正方形 的边长等于.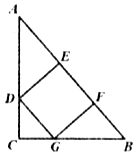 17. 如图,5个同样大小的正方形拼成一个长方形,则 .
17. 如图,5个同样大小的正方形拼成一个长方形,则 .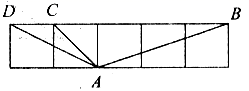 18. 如图,已知在 中, ,分别交边 、 于点D、E,且 将 分成面积相等的两部分.把 沿直线 翻折,点A落在点F的位置上, 交 于点G, 交 于点H,那么 .
18. 如图,已知在 中, ,分别交边 、 于点D、E,且 将 分成面积相等的两部分.把 沿直线 翻折,点A落在点F的位置上, 交 于点G, 交 于点H,那么 .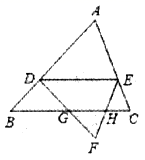
三、解答题
-
19. 已知线段a、b、c,且 .(1)、求 的值;(2)、若线段a、b、c满足 ,求a、b、c的值.20. 已知:如图,在矩形 中, , ,M是边 的中点, ,垂足为E.求:线段 的长.
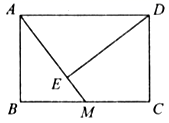 21. 如图,在△ABC中,DE∥BC, = .
21. 如图,在△ABC中,DE∥BC, = .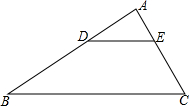 (1)、如果AD=4,求BD的长度;(2)、如果S△ADE=2,求S四边形DBCE的值.22. 如图,在梯形 中, ,对角线 、 交于点O,点E在 上,且 ,已知 , .求 的长.
(1)、如果AD=4,求BD的长度;(2)、如果S△ADE=2,求S四边形DBCE的值.22. 如图,在梯形 中, ,对角线 、 交于点O,点E在 上,且 ,已知 , .求 的长.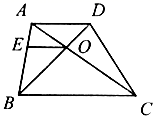 23. 在 中, 是 的中点,且 , ,与 相交于点E, 与 相交于点F.
23. 在 中, 是 的中点,且 , ,与 相交于点E, 与 相交于点F.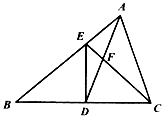 (1)、求证: ;(2)、若 , ,求 的面积.
(1)、求证: ;(2)、若 , ,求 的面积.