辽宁省沈阳市2020年中考数学试卷
试卷更新日期:2020-08-13 类型:中考真卷
一、选择题
-
1. 下列有理数中,比0小的数是( )A、-2 B、1 C、2 D、32. 2020年5月,中科院沈阳自动化所主持研制的“海斗一号”万米海试成功,下潜深度超10900米,刷新我国潜水器最大下潜深度记录.将数据10900用科学记数法表示为( )A、 1.09×103 B、1.09×104 C、10.9×105 D、0.109×1053. 下图是由四个相同的小立方块搭成的几何体,这个几何体的主视图是( )
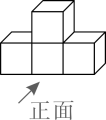 A、
A、 B、
B、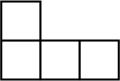 C、
C、 D、
D、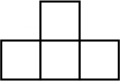 4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,直线 ,且 于点 ,若 ,则 的度数为( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,直线 ,且 于点 ,若 ,则 的度数为( )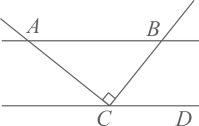 A、65° B、55° C、45° D、35°6. 不等式 的解集是( )A、 B、 C、 D、7. 下列事件中,是必然事件的是( )A、从一个只有白球的盒子里摸出一个球是白球 B、任意买一张电影票,座位号是3的倍数 C、掷一枚质地均匀的硬币,正面向上 D、汽车走过一个红绿灯路口时,前方正好是绿灯8. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定9. 一次函数 的图象经过点 ,点 ,那么该图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,在矩形 中, , ,以点 为圆心, 长为半径画弧交边 于点 ,连接 ,则 的长为( )
A、65° B、55° C、45° D、35°6. 不等式 的解集是( )A、 B、 C、 D、7. 下列事件中,是必然事件的是( )A、从一个只有白球的盒子里摸出一个球是白球 B、任意买一张电影票,座位号是3的倍数 C、掷一枚质地均匀的硬币,正面向上 D、汽车走过一个红绿灯路口时,前方正好是绿灯8. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定9. 一次函数 的图象经过点 ,点 ,那么该图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,在矩形 中, , ,以点 为圆心, 长为半径画弧交边 于点 ,连接 ,则 的长为( )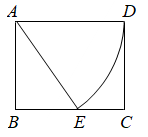 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
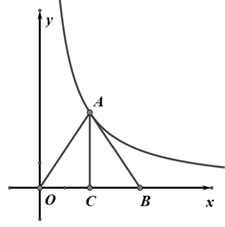
11. 因式分解: .12. 二元一次方程组 的解是。13. 甲、乙两人在相同条件下进行射击练习,每人10次射击成绩的平均值都是7环,方差分别为 ,则两人成绩比较稳定的是.(填“甲”或“乙”)14. 如图,在平面直角坐标系中,O是坐标原点,在 中, 于点C,点A在反比例函数 的图象上,若OB=4,AC=3,则k的值为.
 15. 如图,在平行四边形 中,点M为边 上一点, ,点E,点 分别是 中点,若 ,则 的长为.
15. 如图,在平行四边形 中,点M为边 上一点, ,点E,点 分别是 中点,若 ,则 的长为.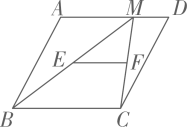 16. 如图,在矩形 中, , ,对角线 相交于点O,点P为边 上一动点,连接 ,以 为折痕,将 折叠,点A的对应点为点E,线段 与 相交于点F.若 为直角三角形,则 的长.
16. 如图,在矩形 中, , ,对角线 相交于点O,点P为边 上一动点,连接 ,以 为折痕,将 折叠,点A的对应点为点E,线段 与 相交于点F.若 为直角三角形,则 的长.
三、解答题
-
17. 计算:18. 沈阳市图书馆推出“阅读沈阳 书香盛京”等一系列线上线下相融合的阅读推广活动,需要招募学生志愿者.某校甲、乙两班共有五名学生报名,甲班一名男生,一名女生;乙班一名男生,两名女生.现从甲、乙两班各随机抽取一名学生作为志愿者,请用列表法或画树状图法求抽出的两名学生性别相同的概率.(温馨提示:甲班男生用 表示,女生用 表示;乙班男生用 表示,两名女生分别用 表示)19. 如图,在矩形 中,对角线 的垂直平分线分别与边 和边 的延长线交于点M,N,与边 交于点E,垂足为点O.
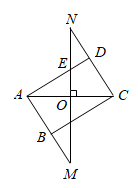 (1)、求证: ;(2)、若 , ,请直接写出 的长为.20. 某市为了将生活垃圾合理分类,并更好地回收利用,将垃圾分为可回收物、厨余垃圾、有害垃圾和其他垃圾四类.现随机抽取该市 吨垃圾,将调查结果制成如下两幅不完整的统计图:
(1)、求证: ;(2)、若 , ,请直接写出 的长为.20. 某市为了将生活垃圾合理分类,并更好地回收利用,将垃圾分为可回收物、厨余垃圾、有害垃圾和其他垃圾四类.现随机抽取该市 吨垃圾,将调查结果制成如下两幅不完整的统计图:
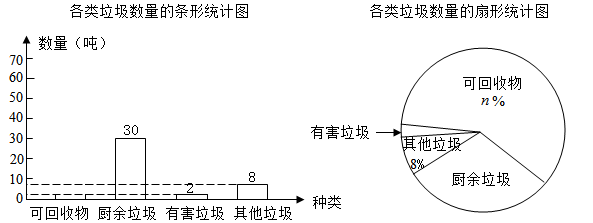
根据统计图提供的信息,解答下列问题:
(1)、 , ;(2)、根据以上信息直接在答题卡中补全条形统计图;(3)、扇形统计图中,厨余垃圾所对应的扇形圆心角的度数为度;(4)、根据抽样调查的结果,请你估计该市200吨垃圾中约有多少吨可回收物.21. 某工程队准备修建一条长 的盲道,由于采用新的施工方式,实际每天修建盲道的长度比原计划增加25%,结果提前2天完成这一任务,原计划每天修建盲道多少米?22. 如图,在 中, ,点 为 边上一点,以点O为圆心, 长为半径的圆与边 相交于点D,连接 ,当 为 的切线时.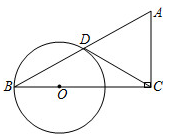 (1)、求证: ;(2)、若 的半径为1,请直接写出 的长为.23. 如图,在平面直角坐标系中, 的顶点O是坐标原点,点A的坐标为 ,点B的坐标为 ,动点P从O开始以每秒1个单位长度的速度沿y轴正方向运动,设运动的时间为t秒( ),过点P作 轴,分别交 于点M,N.
(1)、求证: ;(2)、若 的半径为1,请直接写出 的长为.23. 如图,在平面直角坐标系中, 的顶点O是坐标原点,点A的坐标为 ,点B的坐标为 ,动点P从O开始以每秒1个单位长度的速度沿y轴正方向运动,设运动的时间为t秒( ),过点P作 轴,分别交 于点M,N.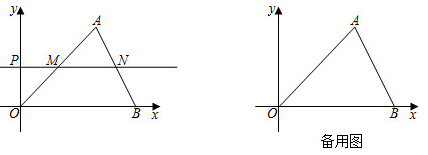 (1)、填空: 的长为 , 的长为(2)、当 时,求点N的坐标:(3)、请直接写出 的长为(用含t的代数式表示);(4)、点 是线段 上一动点(点E不与点 重合), 和 的面积分别表示为 和 ,当 时,请直接写出 (即 与 的积)的最大值为.24. 在 中, ,点P为线段 延长线上一动点,连接 ,将线段 绕点P逆时针旋转,旋转角为 ,得到线段 ,连接 .
(1)、填空: 的长为 , 的长为(2)、当 时,求点N的坐标:(3)、请直接写出 的长为(用含t的代数式表示);(4)、点 是线段 上一动点(点E不与点 重合), 和 的面积分别表示为 和 ,当 时,请直接写出 (即 与 的积)的最大值为.24. 在 中, ,点P为线段 延长线上一动点,连接 ,将线段 绕点P逆时针旋转,旋转角为 ,得到线段 ,连接 .
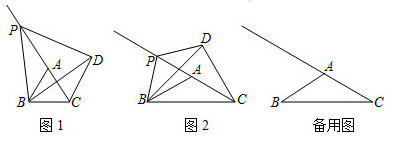 (1)、如图1,当 时,
(1)、如图1,当 时,①求证: ;
②求 的度数:
(2)、如图2,当 时,请直接写出 和 的数量关系为;(3)、当 时,若 时,请直接写出点D到 的距离为.25. 如图,在平面直角坐标系中,O是坐标原点,抛物线 经过点 和点 ,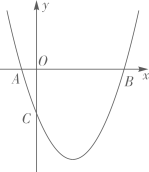 (1)、求抛物线的表达式;(2)、如图,线段 绕原点O逆时针旋转30°得到线段 .过点 作射线 ,点M是射线 上一点(不与点B重合),点M关于x轴的对称点为点N,连接
(1)、求抛物线的表达式;(2)、如图,线段 绕原点O逆时针旋转30°得到线段 .过点 作射线 ,点M是射线 上一点(不与点B重合),点M关于x轴的对称点为点N,连接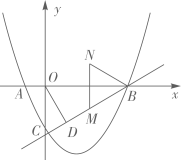
①请直接写出 的形状为_▲_.
②设 的面积为 的面积为是 ,当 时,求点M的坐标;
(3)、如图,在(2)的结论下,过点B作 ,交 的延长线于点E,线段 绕点B逆时针旋转,旋转角为 得到线段 ,过点F作 轴,交射线 于点K, 的角平分线和 的角平分线相交于点G,当 时,请直接写出点G的坐标为.