广西来宾市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-13 类型:期末考试
一、选择题:本大题共12小题,每小题3分,共36分。
-
1. 在Rt△ABC中,∠C=90°,∠A=30°,斜边AB的长5 cm,则BC的长为( )A、2.5 cm B、2 cm C、3 cm D、4 cm2. 若一个多边形的内角和等于1440°,那么这个多边形的边数为( )A、8 B、9 C、10 D、113. 在一次选举中,某候选人的选票没有超过半数,则其频率( )A、大于0.5 B、等于0.5 C、小于0.5 D、小于或等于0.54. 已知△ABC分别满足如下条件:①a=3,b=4,c=5;②a=6,∠A=45°;③a=2,b=2,c=2 ;④∠A=38°,∠B=52°。其中直角三角形有( )A、1个 B、2个 C、3个 D、4个5. 下列一次函数中,y随x值的增大而减小的是( )A、y=2x+1 B、y=3-4x C、y= x+2 D、y=( -2)x6. 在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 在下列命题中,正确的是 ( )A、一组对边平行的四边形是平行四边形 B、有一个角是直角的四边形是矩形 C、有一组邻边相等的平行四边形是菱形 D、对角线互相垂直平分的四边形是正方形8. 如图,△ABC是以BC为斜边的等腰直角三角形,在△BCD中,∠BCD=90°,∠D=60°,E为BD的中点,AB的延长线与CE的延长线交于点F,则∠F的大小为( )
 A、15° B、30° C、45° D、25°9. 已知A,B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),Y表示余下的路程(千米),则y关于x的函数解析式是( )A、y=4x(x>0) B、y=4x-3(x≥ ) C、y=3-4x(x≥0) D、y=3-4x(0≤x≤ )10. 若实数a,b满足ab<0,则一次函数y=ax+b的图象可能是( )A、
A、15° B、30° C、45° D、25°9. 已知A,B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),Y表示余下的路程(千米),则y关于x的函数解析式是( )A、y=4x(x>0) B、y=4x-3(x≥ ) C、y=3-4x(x≥0) D、y=3-4x(0≤x≤ )10. 若实数a,b满足ab<0,则一次函数y=ax+b的图象可能是( )A、 B、
B、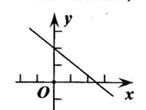 C、
C、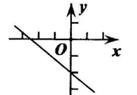 D、
D、 11. 如图,在Rt△ABC中,∠ACB=90°,分别以点B和点C为圆心,大于 BC的长为半径画弧,两弧相交于D,E两点,作直线DE交AB于点F,交BC于点G。连接CF。若AC=3,CG=2,则CF的长为( )
11. 如图,在Rt△ABC中,∠ACB=90°,分别以点B和点C为圆心,大于 BC的长为半径画弧,两弧相交于D,E两点,作直线DE交AB于点F,交BC于点G。连接CF。若AC=3,CG=2,则CF的长为( )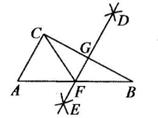 A、2.5 B、3 C、2 D、3.512. 在平面直角坐标系中,一个智能机器人从原点O出发,按向右,向上,向右,向下的方向依次移动,每次移动lm,如此不断重复行走,其行走路线如图所示,第1次移动到A1 , 第2次移动到A2 , 第3次移动到A3 , …,第,2次移动到An , 则△OA2A2018的面积是( )
A、2.5 B、3 C、2 D、3.512. 在平面直角坐标系中,一个智能机器人从原点O出发,按向右,向上,向右,向下的方向依次移动,每次移动lm,如此不断重复行走,其行走路线如图所示,第1次移动到A1 , 第2次移动到A2 , 第3次移动到A3 , …,第,2次移动到An , 则△OA2A2018的面积是( )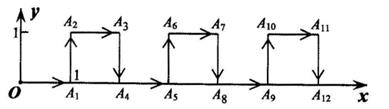 A、504m2 B、504.5m2 C、505.5m2 D、1009m2
A、504m2 B、504.5m2 C、505.5m2 D、1009m2二、填空题:本大题共6小题,每小题3分。共18分。
-
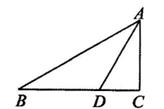
13. 使函数y= 有意义的自变量x的取值范围是。14. 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=。
 15. 若直线y=-2x+3b+2经过第一、二、四象限,则b的取值范围是。16. 一次数学测验后,某班40名学生的成绩被分成5组,第1组至第4组的频数分别为12,10,6,8,则第5组的频率是。17. 如图,EF过平行四边形ABCD对角线的交点D,交AD于点E,交BC于点F。若平行四边形ABCD的周长为18,OE=1.5,则四边形EFCD的周长为。18. 如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点(点P与点B,C不重合),PE⊥AB于E,PF⊥AC于F,则EF的最小值为。
15. 若直线y=-2x+3b+2经过第一、二、四象限,则b的取值范围是。16. 一次数学测验后,某班40名学生的成绩被分成5组,第1组至第4组的频数分别为12,10,6,8,则第5组的频率是。17. 如图,EF过平行四边形ABCD对角线的交点D,交AD于点E,交BC于点F。若平行四边形ABCD的周长为18,OE=1.5,则四边形EFCD的周长为。18. 如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点(点P与点B,C不重合),PE⊥AB于E,PF⊥AC于F,则EF的最小值为。三、解答题:本大题共8小题,共66分。
-
19. 如图,在△ABC中,∠ACB=90°,∠ACD=∠B。
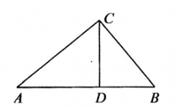 (1)、求证:CD⊥AB;(2)、如果AC=8,BC=6,求CD的长。20. 为创建“国家园林城市”,某校举行了以“爱我来宾”为主题的图片制作比赛,评委会对200名同学的参赛作品打分,参赛者的成绩x均满足50≤x≤100,并将成绩按50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100分段制作成不完整的频数直方图。根据所给信息,解答下列问题:
(1)、求证:CD⊥AB;(2)、如果AC=8,BC=6,求CD的长。20. 为创建“国家园林城市”,某校举行了以“爱我来宾”为主题的图片制作比赛,评委会对200名同学的参赛作品打分,参赛者的成绩x均满足50≤x≤100,并将成绩按50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100分段制作成不完整的频数直方图。根据所给信息,解答下列问题: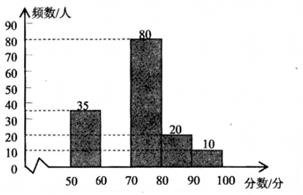 (1)、补全频数直方图;(2)、若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?(3)、比赛共设一、二、三等奖,若只有15%的参赛同学能拿到一等奖,则一等奖的最低分数线是多少?21. △ABC的三个顶点坐标分别是A(-2,-4),B(0,-4),C(1,-1)。
(1)、补全频数直方图;(2)、若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?(3)、比赛共设一、二、三等奖,若只有15%的参赛同学能拿到一等奖,则一等奖的最低分数线是多少?21. △ABC的三个顶点坐标分别是A(-2,-4),B(0,-4),C(1,-1)。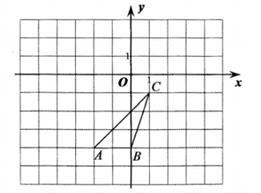
( 1 )画出将△ABC向左平移3个单位得到的△A1B1C1;
( 2 )画出将△ABC绕点D逆时针90。后得到的△A2B2C2。
22. 已知一次函数y=kx-3的图象经过点A(2,1)。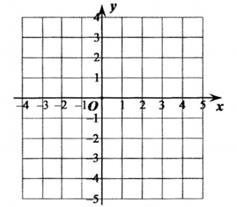 (1)、求k的值;(2)、在图中的直角坐标系画出这个函数的图象;(3)、将此函数的图象向上平移聊个单位后与坐标轴围成的三角形的面积为1,求m的值。23. 如图,在 ABCD中,E,F分别是AB,DC边上的点,且AE=CF。
(1)、求k的值;(2)、在图中的直角坐标系画出这个函数的图象;(3)、将此函数的图象向上平移聊个单位后与坐标轴围成的三角形的面积为1,求m的值。23. 如图,在 ABCD中,E,F分别是AB,DC边上的点,且AE=CF。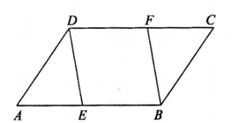 (1)、求证:△ADE≌△CBF;(2)、若∠DEB=90°,求证:四边形DEBF是矩形。24. 如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,顶点C,D都在第一象限内,OA、OB的长分别为4和3。
(1)、求证:△ADE≌△CBF;(2)、若∠DEB=90°,求证:四边形DEBF是矩形。24. 如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,顶点C,D都在第一象限内,OA、OB的长分别为4和3。 (1)、求点D的坐标;(2)、求直线BC的解析式;(3)、在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由。25. 在菱形ABCD中,∠B=60°,点E在射线BC上运动,点F在射线CD上,∠EAF=60°。
(1)、求点D的坐标;(2)、求直线BC的解析式;(3)、在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由。25. 在菱形ABCD中,∠B=60°,点E在射线BC上运动,点F在射线CD上,∠EAF=60°。 (1)、当点E在线段BC上时(如图①),猜想线段AB与EC,CF之间的数量关系,并证明你的结论;(2)、当点E在线段BC的延长线上时(如图②),线段AB与EC,CF之间的数量关系又如何,写出你的结论,并加以证明;(3)、连接DE,当∠ADE为直角,且AB=4时(如图③),求AF的长。26. 某服装店销售10套A品牌运动装和20套B品脾运动装的利润为4000元,销售20套A品牌运动装和10套B品牌运动装的利润为3500元。(1)、该服装店计划一次购进两种品牌的运动装共100套,设服装店购进A品牌运动装x套,这100套运动装的销售总利润为y元,求y关于x的函数关系式;(2)、在(1)的条件下,若B品牌运动装的进货量不超过A品牌的2倍,该服装店购进A、B两种品牌运动装各多少套,才能使销售总利润最大?(3)、实际进货时,厂家对A品牌运动装出厂价下调,且限定超市最多购进A品牌运动装70套,A品牌运动装的进价降低了m(0<m<100)元,若服装店保持两种运动装的售价不变,请你根据以上信息及(2)中的条件,设计出使这100套运动装销售总利润最大的进货方案。
(1)、当点E在线段BC上时(如图①),猜想线段AB与EC,CF之间的数量关系,并证明你的结论;(2)、当点E在线段BC的延长线上时(如图②),线段AB与EC,CF之间的数量关系又如何,写出你的结论,并加以证明;(3)、连接DE,当∠ADE为直角,且AB=4时(如图③),求AF的长。26. 某服装店销售10套A品牌运动装和20套B品脾运动装的利润为4000元,销售20套A品牌运动装和10套B品牌运动装的利润为3500元。(1)、该服装店计划一次购进两种品牌的运动装共100套,设服装店购进A品牌运动装x套,这100套运动装的销售总利润为y元,求y关于x的函数关系式;(2)、在(1)的条件下,若B品牌运动装的进货量不超过A品牌的2倍,该服装店购进A、B两种品牌运动装各多少套,才能使销售总利润最大?(3)、实际进货时,厂家对A品牌运动装出厂价下调,且限定超市最多购进A品牌运动装70套,A品牌运动装的进价降低了m(0<m<100)元,若服装店保持两种运动装的售价不变,请你根据以上信息及(2)中的条件,设计出使这100套运动装销售总利润最大的进货方案。