浙江省绍兴市上虞区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-08-13 类型：期末考试

进入出卷网下载

一、选择题(本题有10小题，每小题3分，共30分。)

1. 如图，在墙面上安装某一管道需经两次拐弯，拐弯后的管道与拐弯前的管道平行。若第一个弯道处∠B=142°，则第二个弯道处∠C的度数为（）

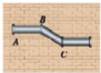A、38° B、142° C、152° D、162°

查看试题解析
2. 某种病毒的直径是120纳米，已知1纳米=10^-9米，用科学记数法表示该病毒的直径，则以下表示正确的是（）

A、120×10^-9米 B、12×10^-8米 C、1.2×10^-7米 D、0.12×10^-6米

查看试题解析
3. 下列调查活动中，适合采用全面调查的是（）

A、某种品牌插座的使用寿命 B、为防控冠状病毒，对从境外来的旅客逐个进行体温检测和隔离 C、了解某校学生课外阅读经典文学著作的情况 D、调查“厉害了，我的国”大型记录电影在线收视率

查看试题解析
4. 下列各式中，计算正确的是（）

A、2a²+a²=3a⁴ B、a³·a²=a⁶ C、a⁶÷a²=a³ D、(ab²)³=a³b⁶

查看试题解析
5. 含30°角的直角三角板与直线a，b的位置关系如图所示，已知a∥b，∠1=35°。则∠ADC的度数是（）

A、35° B、45° C、55° D、65°

查看试题解析
6. 已知x-y= $\frac{1}{2}$ ，xy= $\frac{4}{3}$ ，则xy²-x²y的值是（）

A、 $- \frac{2}{3}$ B、1 C、 $\frac{11}{6}$ D、 $\frac{2}{3}$

查看试题解析
7. 关于a，b的二元一次方程组 ${\begin{cases} 2 a + b = 6.5 \\ 2 a - b = 9.5 \end{cases}$ 的解是 ${\begin{cases} a = 4 \\ b = - 1.5 \end{cases}$ ，则关于x，y的二元一次方程组 ${\begin{cases} 2 （ x+2) + 5 (y - 1) = 6.5 \\ 2 (x + 2) - 5 (y - 1) = 9.5 \end{cases}$ 的解是（）

A、 ${\begin{cases} x = 6 \\ y = - 0.7 \end{cases}$ B、 ${\begin{cases} x = 2 \\ y = - 0.5 \end{cases}$ C、 ${\begin{cases} x = 6 \\ y = 0.7 \end{cases}$ D、 ${\begin{cases} x = 2 \\ y = 0.7 \end{cases}$

查看试题解析
8. 希望中学七年级四个班的学生去阳光公园义务植树，已知在每小时内，5个女生种3棵树，3个男生种5棵树，各班学生人数如图所示，则植树最多的班级是（）

A、七(1)班 B、七(2)班 C、七(3)班 D、七(4)班

查看试题解析
9. 如图，纸片对边AB∥CD，将纸片沿着EF折叠，DF的对应边D'F交AB于点G，FH平分∠CFD'交AC于点H。则结论：①∠AGF=2∠GFE；②∠EGF=∠GFE；③∠CHF=∠GFE；④若∠B'EG=70°，则∠GFE=55°。其中正确结论的个数为（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
10. 定义一种对正整数n的“F”运算：①当n为奇数时，结果为3n+5；②当n为偶数时，结果为 $\frac{n}{2^{k}}$ (其中k是使 $\frac{n}{2^{k}}$ 为奇数的正整数)，并且运算可以重复进行。例如，取n=26，则：

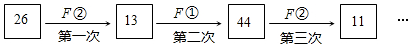
若n=49，则第449次“F运算”的结果是（）

A、98 B、88 C、78 D、68

查看试题解析

二、填空题(本题有10小题，每小题2分，共20分．)

11. 已知方程3x-y=5，用含x的代数式表示y，则y=。

查看试题解析
12. 当x=时，分式 $\frac{x - 1}{3 x - 5}$ 的值为零。

查看试题解析
13. 若a^x·a³=(a²)³ ，则x=。

查看试题解析
14. 如图所示，下列各组数的题序已经填入图中适当的位置。① ${\begin{cases} x = 1 \\ y = 0 \end{cases}$ ；② ${\begin{cases} x = - 2 \\ y = 2 \end{cases}$ ；③ ${\begin{cases} x = - \frac{1}{2} \\ y = 1 \end{cases}$ ；④ ${\begin{cases} x = \frac{1}{2} \\ y = - \frac{1}{2} \end{cases}$ ；则二元一次方程组 ${\begin{cases} x = - y \\ 2 x - 2 = - 3 y \end{cases}$ 的解是。

查看试题解析
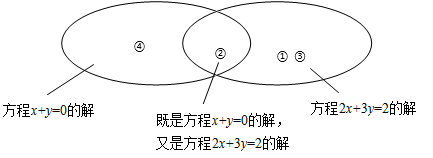15. 小敏对若干名青少年进行最喜爱的运动项目问卷调查后，绘制成如图所示的扇形统计图．已知最喜爱足球运动的人数比最喜爱游泳的人数多40人，则参加这次问卷调查的总人数是。

查看试题解析
16. 如图是边长为a+b的大正方形，通过两种不同的方法计算该大正方形的面积，聪明的你可以得到一个乘法公式，请你用含有字母a，b的等式表达出来。结果是。

查看试题解析
17. 《九章算术》第七卷“盈不足”中记载：“今有共买物，人出八，盈三；人出七，不足四。问人数、物价各几何？”译为：“今有人合伙购物，每人出8钱，会多3钱；每人出7钱，又差4钱。问人数、物价各多少？”通过计算可知，共有人合伙购物。

查看试题解析
18. 如图，已知AB∥CD，∠AFC=120°，∠EAF= $\frac{1}{3}$ ∠EAB，∠ECF= $\frac{1}{3}$ ∠ECD，则∠AEC=度。

查看试题解析
19. 如图，已知天平1和天平2的两端都保持平衡．要使天平3两端也保持平衡，则天平3的右托盘上应放个圆形。

查看试题解析
20. 三位先生A，B，C带着他们的妻子a、b、c到超市购物，至于谁是谁的妻子现在只能从下列条件来推测：他们6人，每人花在买商品的钱数(单位：元)正好等于商品数量的平方，而且每位先生都比自己的妻子多花48元钱，又知先生A比b多买9件商品，先生B比a多买7件商品，则先生A的妻子是。

查看试题解析

三、解答题(本大题有6小题，共50分)

21. 解答下列各题：

(1)、解方程： $\frac{2}{1 - x} + 1 = \frac{x}{1 + x}$

(2)、已知x-3y=0，求分式 $\frac{x^{2} - 3 x y + y^{2}}{x^{2} + y^{2}}$ 的值。

查看试题解析
22. 因式分解：

(1)、ax²-4ay

(2)、3ax²+6axy+3ay²

查看试题解析

23. 为了解学生在新冠肺炎疫情影响期间在家进行体育锻炼的情况，某校通过学生家长微信群以“我最喜欢的体育运动”为主题对全校学生进行随机抽样调查，调查的运动项目有：篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项)。根据调查结果绘制了如下不完整的频数分布表和扇形统计图：

运动项目	频数(人数)	频率
篮球	30	0.25
羽毛球	m	0.20
乒乓球	36	n
跳绳	18	0.15
其它	12	0.10

根据以上图表信息，解答下列问题：

(1)、频数分布表中，m= ， n=；

(2)、在扇形统计图中，“乒乓球”所在扇形圆心角的度数为；

(3)、根据统计数据，结合新冠肺炎疫情防控实际，说说你对参加体育锻炼的一些想法。

查看试题解析

24. 确保室内空气新鲜，一方面是提高生活质量的需要，另一方面也是有效防控新型冠状病毒传播的需要，因而越来越多的居民选购家用空气净化器以净化室内空气。阳光商场抓住商机，从厂家购进了A、B两种型号的净化器共160台，A型号净化器进价是1500元/台，B型号净化器进价是3500元/台，购进两种型号净化器共用去360000元。

(1)、求商场各进了A、B两种型号的净化器多少台？

(2)、为使每台B型号净化器的毛利润是A型号的2倍，且保证售完这160台净化器的毛利润达到110000元，求每台A型号净化器的售价。(注：毛利润=售价-进价)

查看试题解析
25. 如图，在△ABC中，D，E，F三点分别在AB，AC，BC上，过点D的直线与线段EF的交点为点M，已知2∠1-∠2=150°，2∠2-∠1=30°。

(1)、试说明DM∥AC的理由；

(2)、若DE∥BC，∠C=50°，求∠3的度数。

查看试题解析
26. 如图

(1)、问题情境：
如图1，已知AB∥CD，∠APC=108°。求∠PAB+∠PCD的度数。

经过思考，小敏的思路是：如图2，过P作PE∥AB，根据平行线有关性质，可得∠PAB+∠PCD=。

(2)、问题迁移：如图3，AD∥BC，点P在射线OM上运动，∠ADP=∠α，∠BCP=∠β。
当点P在A、B两点之间运动时，∠CPD、∠α、∠β之间有何数量关系？请说明理由。

(3)、如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合)，请你直接写出∠CPD、∠α、∠β之间的数量关系。

(4)、问题拓展：
如图4，MA₁∥NA_n ， A₁-B₁-A₂-…-B_n-1-A_n ，是一条折线段，依据此图所含信息，把你所发现的结论，用简洁的数学式子表达为。

查看试题解析