江苏省苏州市吴中区2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2020-08-13 类型：期中考试

进入出卷网下载

一、单选题

1. 如图所示的图案分别是三菱、大众、奥迪、奔驰汽车的车标，其中可以看着是由“基本图案”经过平移得到的是（）

A、奥迪 B、本田 C、大众 D、铃木

查看试题解析
2. 下列各式中计算正确的是（）

A、 ${(x^{2})}^{3}$ = x⁵ B、 ${(- a^{2})}^{3} = - a^{6}$ C、 $b^{3} \cdot b^{3} = b^{9}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
3. 流感病毒的直径为0.00000012m，该数值用科学记数法表示为（）

A、 $1.2 \times 10^{- 8}$ m B、 $1.2 \times 10^{- 7}$ m C、 $12 \times 10^{- 7}$ m D、 $1.2 \times 10^{7}$ m

查看试题解析
4. 下列从左到右的变形，是因式分解的是（）

A、 $(a + 3) (a - 3) = a^{2} - 9$ B、 $x^{2} + x - 5 = (x - 2) (x + 3) + 1$ C、 $a^{2} b + a b^{2} = a b (a + b)$ D、 $x^{2} - 1 = {(x - 1)}^{2}$

查看试题解析
5. 如图，点 E 在 BC 的延长线上，下列条件中能判断AB//CD的是（）

A、∠3=∠4 B、∠D=∠DCE C、∠B=∠D D、∠1=∠2

查看试题解析
6. 若多项式a²+kab+4b²是完全平方式，则常数k的值为（　　）

A、2 B、4 C、±2 D、±4

查看试题解析
7. 方程组 ${\begin{cases} x = y + 5 \\ 2 x - y = 5 \end{cases}$ 的解满足方程x＋y－a=0，那么a的值是（）

A、5 B、-5 C、3 D、-3

查看试题解析
8. 如图，在边长为a的正方形上剪去一个边长为b的小正方形（a＞b），把剩下的部分剪拼成一个梯形，分别计算这两个图形阴影部分的面积，由此可以验证的等式是（）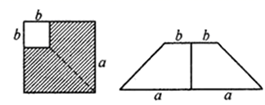

A、（a﹣b）²=a²﹣2ab+b² B、（a+b）²=a²+2ab+b² C、a²﹣b²=（a+b）（a﹣b） D、a²﹣ab=a（a﹣b）

查看试题解析
9. 李明同学早上骑自行车上学，中途因道路施工步行一段路，到学校共用时15分钟．他骑自行车的平均速度是250米/分钟，步行的平均速度是80米/分钟．他家离学校的距离是2900米．如果他骑车和步行的时间分别为x、y分钟，列出的方程是（）

A、 ${\begin{array}{l} x + y = \frac{1}{4} \\ 250 x + 80 y = 2900 \end{array}$ B、 ${\begin{array}{l} x + y = 15 \\ 80 x + 250 y = 2900 \end{array}$ C、 ${\begin{array}{l} x + y = \frac{1}{4} \\ 80 x + 250 y = 2900 \end{array}$ D、 ${\begin{array}{l} x + y = 15 \\ 250 x + 80 y = 2900 \end{array}$

查看试题解析
10. 如图，△ABC的角平分线CD、BE相交于F，∠A=90°，EG∥BC，且CG⊥EG于G，下列结论：
①∠CEG=2∠DCB；②∠DFB= $\frac{1}{2}$ ∠CGE；③∠ADC=∠GCD；④CA平分∠BCG．
其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 计算： ${(a^{5})}^{2} =$ .

查看试题解析
12. n边形的外角和是．

查看试题解析
13. 在△ABC中，若∠A﹣∠B=∠C，则此三角形是三角形．

查看试题解析
14. 如果 ${\begin{matrix} x = 3 \\ y = - 5 \end{matrix}$ ，是方程组 ${\begin{matrix} x + y = m \\ 2 x - y = n \end{matrix}$ 的解，则 $m - n =$ .

查看试题解析
15. 已知 $a^{m} = 2, a^{n} = 3$ ，则 $a^{3 m + 2 n} =$ .

查看试题解析
16. 计算： $5^{2019} \times {0.2}^{2020} =$ .

查看试题解析
17. 如图，两个正方形的边长分别为a、b，如果a＋b＝7，ab＝10，则阴影部分的面积为.

查看试题解析
18. 如图，在△ABC中，∠C=90°，BC=8cm，AC=6cm，点E是BC的中点，动点P从A点出发以每秒2cm的速度沿A→C→B运动，设点P运动的时间是t秒，那么当t= ， △APE的面积等于6.

查看试题解析

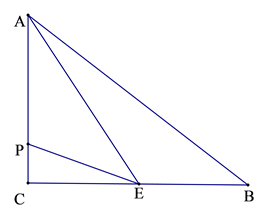
三、解答题

19. 计算或化简:

(1)、 $| - 1 | + {(- 2)}^{3} + {(7 - π)}^{0} - {(\frac{1}{3})}^{- 1}$ ；

(2)、 $3 a^{3} \cdot 2 a^{6} - 3 a^{12} \div a^{3}$ ；

(3)、 ${(x + y)}^{2} + (x - y) (x + 2 y)$ ；

(4)、 $(3 a + b - 2) (3 a - b + 2)$ .

查看试题解析
20. 因式分解:

(1)、 $x^{2} - 4$ ；

(2)、 $a^{3} - 2 a^{2} + a$ .

查看试题解析
21. 解方程组： ${\begin{matrix} 2 x + y = 1 ① \\ 5 x - 3 y = 8 ② \end{matrix}$ ．

查看试题解析
22. 如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点.

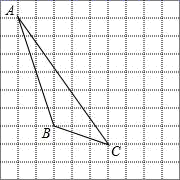
（ 1 ）画出△ABC向右平移4个单位后得到的△A₁B₁C₁；

（ 2 ）图中AC与A₁C₁的关系是：_▲_.

（ 3 ）画出△ABC的AB边上的高CD；垂足是D；

（ 4 ）图中△ABC的面积是_▲_.

查看试题解析
23. 已知 $(x + a) (x - 2)$ 的结果中不含关于字母 $x$ 的一次项.先化简，再求： ${(a + 1)}^{2} + (2 - a) (2 + a)$ 的值.

查看试题解析
24. 关于x、y的两个方程组 ${\begin{array}{l} a x - 2 b y = 2 \\ 2 x - y = 7 \end{array}$ 和 ${\begin{array}{l} 3 a x - 5 b y = 9 \\ 3 x - y = 11 \end{array}$ 具有相同的解，则a、b的值是多少？

查看试题解析
25. 填写下列空格完成证明：如图， EF∥AD ， ∠1 = ∠2 ， ∠BAC = 70° ，求∠AGD .
解：

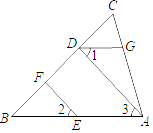
∵ EF∥AD ，

∴ ∠2 = ▲ .（   ）

∵ ∠1 = ∠2 ，

∴ ∠1 = ∠3.（   ）

∴▲ ∥ ▲ .（   ）

∴ ∠BAC + ▲ = 180° .（   ）

∵ ∠BAC = 70° ，

∴ ∠AGD =▲ ° .

查看试题解析
26. 我市某农场有A、B两种型号的收割机共20台，每台A型收割机每天可收大麦100亩或者小麦80亩，每台B型收割机每天可收大麦80亩或者小麦60亩，该农场现有19 000亩大麦和11 500亩小麦先后等待收割．先安排这20台收割机全部收割大麦，并且恰好10天时间全部收完.

(1)、问A、B两种型号的收割机各多少台？

(2)、由于气候影响，要求通过加班方式使每台收割机每天多完成10%的收割量，问这20台收割机能否在一周时间内完成全部小麦收割任务？

查看试题解析
27. “a²≥0”这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式.例如：x²+4x+5＝x²+4x+4+1＝（x+2）²+1，∵（x+2）²≥0，∴（x+2）²+1≥1，∴x²+4x+5≥1.试利用“配方法”解决下列问题：

(1)、填空：x²﹣4x+5＝（x）²+；

(2)、已知x²﹣4x+y²+2y+5＝0，求x+y的值；

(3)、比较代数式：x²﹣1与2x﹣3的大小.

查看试题解析
28. 如图，AD∥BC，∠B＝∠D＝50°，点E、F在BC上，且满足∠CAD＝∠CAE，AF平分∠BAE.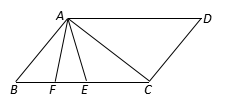

(1)、∠CAF＝°；

(2)、若平行移动CD，那么∠ACB与∠AEB度数的比值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值；

(3)、在平行移动CD的过程中，是否存在某种情况，使∠AFB＝∠ACD？若存在，求出∠ACD度数；若不存在，说明理由.

查看试题解析