江苏省苏州市常熟市2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2020-08-13 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、（a³）⁴=a⁷ B、a²+a²=2a⁴ C、（-a²b³）²=a⁴b⁶ D、a³÷a³=a

查看试题解析
2. 下列方程是二元一次方程的是（）

A、 $\frac{x}{2} + \frac{y}{3} = 5$ B、xy=2 C、 $\frac{2}{x}$ +y=1 D、x²+x-2=0

查看试题解析
3. 若三角形的两条边的长度是4cm和7cm，则第三条边的长度可能是（）

A、2cm B、3cm C、8cm D、12cm

查看试题解析
4. 下列各式从左到右的变形属于因式分解的是（）

A、（x+2）（x-3）=x²-x-6 B、6xy=2x²·3y³ C、x²+2x+1=x（x²+2）+1 D、x²-9=（x-3）（x+3）

查看试题解析
5. 一副三角板如图放置，它们的直角顶点A重合，∠C=45°，∠E=30°若AC//DE，则∠1的度数为（）

A、90° B、75° C、60° D、45°

查看试题解析
6. 若x²+（k+2）x+9是完全平方式，则k的值为（）

A、4 B、±4 C、-8 D、4或-8

查看试题解析
7. 若x-3与一个多项式的乘积为x²+x-12，则这个多项式为（）

A、x+4 B、x-4 C、x-9 D、x+6

查看试题解析
8. 把一堆练习本分给学生，如果每名学生分4本，那么多4本；如果每名学生分5本，那么最后1名学生只有3本.设有x名学生，y本书，根据题意，可列方程组为（）

A、 ${\begin{array}{l} 4 x + 4 = y \\ 5 x + 3 = y \end{array}$ B、 ${\begin{array}{l} 4 x - 4 = y \\ 5 x - 3 = y \end{array}$ C、 ${\begin{matrix} 4 x + 4 = y \\ 5 (x - 1) + 3 = y \end{matrix}$ D、 ${\begin{matrix} 4 x - 4 = y \\ 5 (x - 1) + 3 = y \end{matrix}$

查看试题解析
9. 若 $a = {(- 3)}^{- 1} *, b = {(- 0.1)}^{2}, c = {(- \frac{1}{2})}^{- 2}$ ，d=（-0.3）⁰ ，则（）

A、a<b<c<d B、a<b<d<c C、b<c<d<a D、b<d<a<c

查看试题解析
10. 若△ABC内有一个点P₁ ，当P₁、A、B、C没有任何三点在同一直线上时，如图1，可构成3个互不重叠的小三角形；若△ABC内有两个点P₁、P₂ ，其它条件不变，如图2，可构成5个互不重叠的小三角形：……若△ABC内有n个点，其它条件不变，则构成若干个互不重叠的小三角形，这些小三角形的内角和为（）

A、n·180° B、（n+2）·180° C、（2n-1）·180° D、（2n+1）·180°

查看试题解析

二、填空题

11. 有一种病毒，其直径为0.000000078米，将0.000000078用科学记数法表示为

查看试题解析
12. 计算： $2 a \cdot 3 a b =$ .

查看试题解析
13. 一个多边形的内角和等于外角和的4倍，这个多边形的边数为

查看试题解析
14. 如图，△ABC中，∠A=50°，点D、E分别在AB、AC上，则∠1+∠2+∠3+∠4=

查看试题解析
15. 已知a^m=32，aⁿ=2，则a^m+2n=

查看试题解析
16. 已知关于x、y的二元一次方程组 ${\begin{array}{l} a x + b y = 2 \\ b x + a y = 7 \end{array}$ 的解是 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ ，那么a+b=

查看试题解析
17. 若（x+2）（x²-ax+3）的乘积中不含x的一次项，则a=

查看试题解析
18. 如图，AD是△ABC的中线，BE是△ABD的中线，EF⊥BC于点出F.若S_△_ABC=12，BD=2，则EF=

查看试题解析

三、解答题

19. 计算：

(1)、 $- 1^{2020} + {(\frac{1}{2})}^{- 2} + {(π - 3)}^{0}$

(2)、a（-a）³+（2a²）³÷a²

(3)、（2x-y）²-（x+2y）（x-2y）.

查看试题解析
20. 分解因式：

(1)、16x²-1；

(2)、12a²b-12ab+3b；

(3)、x²（a-2b）+y²（2b-a）.

查看试题解析
21. 解方程组：

(1)、 ${\begin{array}{l} 2 x - y = 4 \\ 3 x + 2 y = - 1 \end{array}$

(2)、 ${\begin{array}{l} x + z = 5 \\ 3 x - y + z = 8 \\ x + y - 2 z = - 3 \end{array}$

查看试题解析
22. 先化简，再求值：2（x-1）（2x+1）-（x+1）²+（x-3）（x+3），其中x=2.

查看试题解析
23. 在如图所示的正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的顶点都在正方形网格的格点（网格线的交点）上.

(1)、①画出△ABC先向右平移5个单位长度，再向上平移2个单位长度所得的△A₁B₁C₁；
②画出△ABC的中线AD；
③画出△ABC的高CE所在直线，标出垂足E：

(2)、在（1）的条件下，线段AA₁和CC₁的关系是

查看试题解析
24. 如图，在△ABC中，点D在BC上，∠ADB=∠BAC，BE平分∠ABC，过点E作EF/AD，交BC于点F.

(1)、求证：∠BAD=∠C；

(2)、若∠C=20°，∠BAC=110°，求∠BEF的度数.

查看试题解析
25. 已知关于x、y的二元一次方程组 ${\begin{matrix} 3 x - y = - 4 \\ 5 x - 2 y = 2 k - 1 \end{matrix}$ 的解x与y互为相反数，求k的值.

查看试题解析
26. 如图1，有A型、B型正方形卡片和C型长方形卡片各若干张.

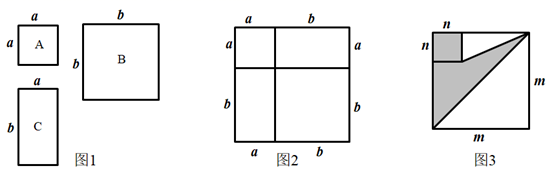(1)、用1张A型卡片，1张B型卡片，2张C型卡片拼成一个正方形，如图2，用两种方法计算这个正方形面积，可以得到一个等式，请你写出这个等式；

(2)、选取1张A型卡片，10张C型卡片，张B型卡片，可以拼成一个正方形，这个正方形的边长用含a，b的代数式表示为；

(3)、如图3，两个正方形边长分别为m、n，m+n=10，mn=19，求阴影部分的面积.

查看试题解析

27. 某集团购买了150吨物资打算运往某地支援，现有甲、乙、丙三种车型供选择，每辆汽车的运载能力和运费如下表所示：（假设每辆车均满载）

车型	甲	乙	丙
汽车运载量（吨/辆）	5	8	10
汽车运费（元/辆）	1000	1200	1500

(1)、若全部物资都用甲、乙两种车型来运送，需运费24000元，问分别需甲、乙两种车型各多少辆？

(2)、若该集团决定用甲、乙、丙三种汽车共18辆同时参与运送，请你写出可能的运送方案，并帮助该集团找出运费最省的方案（甲、乙、丙三种车辆均要参与运送）.

查看试题解析

28. 如图1，已知∠MON=60°，A、B两点同时从点O出发，点A以每秒x个单位长度沿射线ON匀速运动，点B以每秒y个单位长度沿射线OM匀速运动.

(1)、若运动1s时，点A运动的路程比点B运动路程的2倍还多1个单位长度，运动3s时，点A、点B的运动路程之和为12个单位长度，则x= ， y=；

(2)、如图2，点C为△ABO三条内角平分线交点，连接BC、AC，在点A、B的运动过程中，∠ACB的度数是否发生变化？若不发生变化，求其值；若发生变化，请说明理由；

(3)、如图3，在（2）的条件下，连接OC并延长，与∠ABM的角平分线交于点P，与AB交于点Q.
①试说明∠PBQ=∠ACQ；

②在△BCP中，如果有一个角是另一个角的2倍，请写出∠BAO的度数.

查看试题解析