江苏省南通市如东县2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期:2020-08-13 类型:期中考试
一、单选题
-
1. 下列各数中,无理数是( )A、 B、 C、 D、3.14159265342. 若x<y,则下列不等式中一定成立的是( )A、x2<y2 B、-3x<-3y C、 > D、1-x>1-y3. 不等式组 的解集在数轴上表示为( )A、
 B、
B、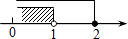 C、
C、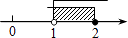 D、
D、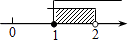 4. 下列四个命题是真命题的是( )A、内错角相等 B、如果两个角的和是180°,那么这两个角是邻补角 C、在同一平面内,平行于同一条直线的两条直线互相平行 D、在同一平面内,垂直于同一条直线的两条直线互相垂直5. 估计 的值在 ( )A、-2到-1之间 B、-1到0之间 C、0到1之间 D、1到2之间6. 如图,直线 被 所截, ,若 ,则 的度数为( )
4. 下列四个命题是真命题的是( )A、内错角相等 B、如果两个角的和是180°,那么这两个角是邻补角 C、在同一平面内,平行于同一条直线的两条直线互相平行 D、在同一平面内,垂直于同一条直线的两条直线互相垂直5. 估计 的值在 ( )A、-2到-1之间 B、-1到0之间 C、0到1之间 D、1到2之间6. 如图,直线 被 所截, ,若 ,则 的度数为( )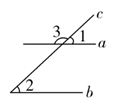 A、 B、 C、 D、7. 若关于x,y的方程组 的解也是二元一次方程x-2y=1的解,则m的值为( )A、 B、 C、 D、18. 关于x的不等式:a<x<2有两个整数解,则a的取值范围是( )A、0<a≤1 B、0≤a<1 C、-1<a≤0 D、-1≤a<09. 已知点P的坐标为(a,b)(a>0),点Q的坐标为(c,2),且|a-c|+ =0,将线段PQ向右平移a个单位长度,其扫过的面积为24,那么a+b+c的值为( )A、12 B、14 C、16 D、2010. 在平面直角坐标系中,点A(a,0),点B(2﹣a,0),且A在B的左边,点C(1,﹣1),连接AC,BC,若在AB,BC,AC所围成区域内(含边界),横坐标和纵坐标都为整数的点的个数为4个,那么a的取值范围为( )A、﹣1<a≤0 B、0≤a<1 C、﹣1<a<1 D、﹣2<a<2
A、 B、 C、 D、7. 若关于x,y的方程组 的解也是二元一次方程x-2y=1的解,则m的值为( )A、 B、 C、 D、18. 关于x的不等式:a<x<2有两个整数解,则a的取值范围是( )A、0<a≤1 B、0≤a<1 C、-1<a≤0 D、-1≤a<09. 已知点P的坐标为(a,b)(a>0),点Q的坐标为(c,2),且|a-c|+ =0,将线段PQ向右平移a个单位长度,其扫过的面积为24,那么a+b+c的值为( )A、12 B、14 C、16 D、2010. 在平面直角坐标系中,点A(a,0),点B(2﹣a,0),且A在B的左边,点C(1,﹣1),连接AC,BC,若在AB,BC,AC所围成区域内(含边界),横坐标和纵坐标都为整数的点的个数为4个,那么a的取值范围为( )A、﹣1<a≤0 B、0≤a<1 C、﹣1<a<1 D、﹣2<a<2二、填空题
-
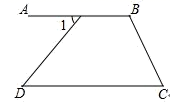
11. 化简: = .12. 已知方程组 ,则x-y=.13. 在平面直角坐标系中,点M(a-3,a+4),点N(5,9),若MN∥y轴,则a=.14. 如图,AB∥CD,∠1=48°,∠C和∠D互余,则∠B=°.
 15. 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过80%,那么明年空气质量良好的天数比去年至少要增加天.16. 如果点P(-3a-2,a2)在第二象限,那么a的取值范围是.17. 若2m+1 的值同时大于 3m-2和 m+2的值,且m为整数,则 3m-5 =.18. 有这样的一列数a1、a2、a3、…、an , 满足公式an=a1+(n-1)d,已知a2=197,a5=188,若ak>0,ak+1<0,则k的值为.
15. 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过80%,那么明年空气质量良好的天数比去年至少要增加天.16. 如果点P(-3a-2,a2)在第二象限,那么a的取值范围是.17. 若2m+1 的值同时大于 3m-2和 m+2的值,且m为整数,则 3m-5 =.18. 有这样的一列数a1、a2、a3、…、an , 满足公式an=a1+(n-1)d,已知a2=197,a5=188,若ak>0,ak+1<0,则k的值为.三、解答题
-
19.(1)、计算: - + -|2- |;(2)、解方程组 .20. 若m是不等式组 的最大整数解,求:1+m+m2+…+m2020的值.21. 如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(-2,1),B(-3,-2),C(1,-2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
 (1)、在图中画出△A1B1C1;(2)、点A1 , B1 , C1的坐标分别为、、;(3)、若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.22. 填空完成推理过程:
(1)、在图中画出△A1B1C1;(2)、点A1 , B1 , C1的坐标分别为、、;(3)、若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.22. 填空完成推理过程:如图,BCE,AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,求证AD∥BE.
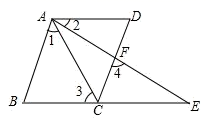
证明:∵AB∥CD(已知)
∴∠4=∠BAE( )
∵∠3=∠4(已知)
∴∠3=∠ ▲ (等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF( )
即∠BAF=∠CAD
∴∠3=∠ ▲ (等量代换)
∴AD∥BE( )
23. 平面直角坐标系xOy中,有点P(a,b),实数a,b,m满足以下两个等式:2a﹣3m+1=0,3b﹣2m﹣16=0
(1)、当a=1时,点P到x轴的距离为;(2)、若点P落在x轴上,点P平移后对应点为P′(a+15,b+4),求点P和P′的坐标;(3)、当a≤4<b时,求m的最小整数值.24. 新冠肺炎疫情期间,某口罩厂为生产更多的口罩满足疫情防控需求,决定拨款456万元购进A,B两种型号的口罩机共30台.两种型号口罩机的单价和工作效率分别如下表:单价/万元
工作效率/(只/h)
A种型号
16
4000
B种型号
14.8
3000
(1)、求购进A,B两种型号的口罩生产线各多少台.(2)、现有200万只口罩的生产任务,计划安排新购进的口罩机共15台同时进行生产.若工厂的工人每天工作8h,则至少租用A种型号的口罩机多少台才能在5天内完成任务?25. 已知:点A、C、B不在同一条直线上,AD∥BE. (1)、如图①,当∠A=48°,∠B=128°时,求∠C的度数;(2)、如图②,AQ、BQ分别为∠DAC、∠EBC的平分线所在直线,试探究∠C与∠AQB的数量关系;(3)、如图③,在(2)的前提下,且有AC∥QB,QP⊥PB,直接写出∠DAC:∠ACB:∠CBE的值.26. 在同一平面内,若一个点到一条直线的距离不大于1,则称这个点是该直线的“伴侣点”.在平面直角坐标系中,已知点M(1,0),过点M作直线l平行于y轴.(1)、试判断点A(-1,a)是否是直线l的“伴侣点”?请说明理由;(2)、若点P(2m-5,8)是直线l的“伴侣点”,求m的取值范围;(3)、若点A(-1,a)、B(b,2a)、C(- ,a-1)是平面直角坐标系中的三个点,将三角形ABC进行平移,平移后点A的对应点为D,点B的对应点为E,点C的对应点为F.若点F刚好落在直线l上,F的纵坐标为a+b,点E落在x轴上,且三角形MFD的面积为 ,试判断点B是否是直线l的“伴侣点”?请说明理由.
(1)、如图①,当∠A=48°,∠B=128°时,求∠C的度数;(2)、如图②,AQ、BQ分别为∠DAC、∠EBC的平分线所在直线,试探究∠C与∠AQB的数量关系;(3)、如图③,在(2)的前提下,且有AC∥QB,QP⊥PB,直接写出∠DAC:∠ACB:∠CBE的值.26. 在同一平面内,若一个点到一条直线的距离不大于1,则称这个点是该直线的“伴侣点”.在平面直角坐标系中,已知点M(1,0),过点M作直线l平行于y轴.(1)、试判断点A(-1,a)是否是直线l的“伴侣点”?请说明理由;(2)、若点P(2m-5,8)是直线l的“伴侣点”,求m的取值范围;(3)、若点A(-1,a)、B(b,2a)、C(- ,a-1)是平面直角坐标系中的三个点,将三角形ABC进行平移,平移后点A的对应点为D,点B的对应点为E,点C的对应点为F.若点F刚好落在直线l上,F的纵坐标为a+b,点E落在x轴上,且三角形MFD的面积为 ,试判断点B是否是直线l的“伴侣点”?请说明理由.