浙江省绍兴市新昌县2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2020-08-13 类型：期中考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{2 a - 1}$ 有意义时， $x$ 的取值范围是（）

A、 $a$ < $\frac{1}{2}$ B、 $a$ ≤ $\frac{1}{2}$ C、 $a$ > $\frac{1}{2}$ D、 $a$ ≥ $\frac{1}{2}$

查看试题解析
2. 下列图形是中心对称图形的个数有（）

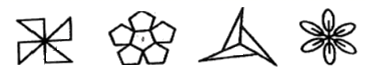A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 为了比较甲、乙两块地的小麦哪块长得更整齐，应选择的统计量为（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
4. 正方形具有而菱形不一定具有的性质是（）

A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分一组对角

查看试题解析
5. 用下列哪种方法解方程3x²＝16x最合适（）

A、开平方法 B、配方法 C、因式分解法 D、公式法

查看试题解析
6. 一元二次方程4x²﹣2x+ $\frac{1}{4}$ =0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
7. 用反证法证明命题“钝角三角形中必有一个内角小于45°”时，首先应该假设这个三角形中（　　）

A、有一个内角小于45° B、每一个内角都小于45° C、有一个内角大于等于45° D、每一个内角都大于等于45°

查看试题解析
8. 如图，在给定的一张平行四边形纸片上按如下操作：连结AC，作AC的垂直平分线MN分别交AD、AC、BC于M、O、N，连结AN，CM，则四边形ANCM是（）

A、矩形 B、菱形 C、正方形 D、无法判断

查看试题解析
9. 某建筑工程队在工地一边靠墙处，用81米长的铁栅栏围成三个相连的长方形仓库，仓库总面积为440平方米. 为了方便取物，在各个仓库之间留出了1米宽的缺口作通道，在平行于墙的一边留下一个1米宽的缺口作小门. 若设AB=x米，则可列方程（）

A、x（81-4x）=440 B、x（78-2x）=440 C、x（84-2x）=440 D、x（84-4x）=440

查看试题解析
10. 如图，以▱ABCD 的四条边为边，分别向外作正方形，连结 EF，GH，IJ，KL.如果▱ABCD 的面积为 8，则图中阴影部分四个三角形的面积和为（）

A、8 B、12 C、16 D、20

查看试题解析

二、填空题

11. $\sqrt{20}$ 、 $\frac{\sqrt{2}}{3}$ 、 $\sqrt{\frac{1}{a}}$ 、 $- \sqrt{0.1}$ 、 $\sqrt{x^{3}}$ 中，是最简二次根式的是.

查看试题解析
12. 已知多边形的内角和等于外角和的三倍，则边数为.

查看试题解析
13. 已知 $x^{k^{2} - 2} - \sqrt{1 - k} x + \frac{1}{2}$ =0 是关于 x 的一元二次方程，则 k 为.

查看试题解析
14. 小王参加某企业招聘测试，他的笔试、面试、技能操作得分分别为85分，80分，90分，若依次按照2：3：5的比例确定成绩，则小王的成绩分.

查看试题解析
15. 把方程x²﹣4x+1＝0化成（x﹣m）²＝n的形式，m，n均为常数，则mn的值为．

查看试题解析
16. 如图，在Rt△ABC中，∠ACB=90°，点D、E分别是AB、AC的中点，点F是AD的中点.若AB=10，则EF=.

查看试题解析
17. 如图，在正方形ABCD中，边长为a，点O是对角线AC的中点，点E是BC边上的一个动点，OE⊥OF交AB边于点F，点G，H分别是点E，F关于直线AC的对称点，点E从点C运动到点B时，则图中阴影部分的面积是.

查看试题解析
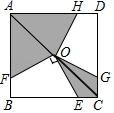18. 如图，一个正方形内两个相邻正方形的面积分别为 4 和 2，它们都有两个顶点在大正方形的边上且组成的图形为轴对称图形，则图中阴影部分的面积为.

查看试题解析

三、解答题

19. 计算：

(1)、 $2 \times (1 - \sqrt{2}) + \sqrt{8}$ ；

(2)、解方程：2x²+3x=0.

查看试题解析
20. 如图，AC 是▱ABCD 的一条对角线，BE⊥AC，DF⊥AC，垂足分别为 E，F.

(1)、求证：△ADF≌△CBE；

(2)、求证：四边形 DFBE 是平行四边形.

查看试题解析
21. 某初中要调查学校学生（总数 1000 人）双休日课外阅读情况，随机调查了一部分学生，调查得到的数据分别制成频数直方图（如图 1）和扇形统计图（如图 2）.

(1)、请补全上述统计图（直接填在图中）；

(2)、试确定这个样本的中位数和众数；

(3)、请估计该学校 1000 名学生双休日课外阅读时间不少于 4 小时的人数.

查看试题解析
22. 已知方程：x $^{2}$ ﹣2x﹣8=0，解决一下问题：

(1)、不解方程判断此方程的根的情况；

(2)、请按要求分别解这个方程：①配方法；②因式分解法.

(3)、这些方法都是将解转化为解；

(4)、尝试解方程： $x^{3} + 2 x^{2} + x = 0$ .

查看试题解析
23. 我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”.

(1)、已知：如图1，四边形ABCD的顶点A，B，C在网格格点上，请你在如下的5x7的网格中画出3个不同形状的等邻边四边形ABCD，要求顶点D在网格格点上；

(2)、如图2，矩形ABCD中，AB= $\frac{20}{7}$ ，BC=5，点E在BC边上，连结DE画AF DE于点F，若DE= $\frac{5}{4}$ CD，找出图中的等邻边四边形；

(3)、如图3，在Rt $△$ ABC中， $∠$ ACB=90°，AB=4，AC=2，D是BC的中点，点M是AB边上一点，当四边形ACDM是“等邻边四边形”时，求BM的长.

查看试题解析
24. 在矩形 ABCD 中，AB＝3，BC＝4，E、F 是对角线 AC 上的两个动点，分别从 A、C 同时出发相向而行，速度均为每秒 1 个单位长度，运动时间为 t 秒，其中 0≤t≤5 .

(1)、若 G，H 分别是 AB，DC中点，求证：四边形 EGFH 是平行四边形（E、F 相遇时除外）；

(2)、在（1）条件下，若四边形 EGFH 为矩形，求 t 的值；

(3)、若 G，H 分别是折线 A－B－C，C－D－A 上的动点，与 E，F 相同的速度同时出发，若四边形 EGFH 为菱形，求 t 的值.

查看试题解析