浙江省宁波市鄞州区七校联考2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2020-08-13 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{0.8}$ C、 $\sqrt{5}$ D、 $\sqrt{4}$

查看试题解析
3. 下列计算正确的是（　　）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{3} + \sqrt{2} = \sqrt{6}$ C、 $\sqrt{8} - \sqrt{2} = \sqrt{6}$ D、 $\sqrt{8} \div \sqrt{2}$ ＝2

查看试题解析
4. 将方程x²－6x＋1＝0配方后，原方程变形（）

A、(x－3)²＝8 B、(x－3)²＝－8 C、(x－3)²＝9 D、(x－3)²＝－9

查看试题解析
5. 一个多边形内角和是900°，则这个多边形的边数是（）

A、7 B、6 C、5 D、4

查看试题解析
6. 王老师对甲、乙两人五次数学成绩进行统计，两人平均成绩均为90分，方差S_甲²=12，S_乙²=51，则下列说法正确的是（　　）

A、甲、乙两位同学的成绩一样稳定 B、乙同学的成绩更稳定 C、甲同学的成绩更稳定 D、不能确定

查看试题解析
7. 某工厂一月份生产零件50万个，已知第一季度共生产零件182万个，若设该厂平均每月的增长率为x，可以列出方程（）

A、 $50 {(1 + x)}^{2} = 182$ B、 $50 (1 + 3 x) = 182$ C、 $50 [1 + (1 + x) + {(1 + x)}^{2}] = 182$ D、 $182 {(1 - x)}^{2} = 50$

查看试题解析
8. 利用反证法证明命题“四边形中至少有一个角是钝角或直角”时，应假设（）

A、四边形中至多有一个内角是钝角或直角 B、四边形中所有内角都是锐角 C、四边形的每一个内角都是钝角或直角 D、四边形中所有内角都是直角

查看试题解析
9. 如图，△ABC中，AB=4，AC=3，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，则线段EF的长为（）

A、1 B、 $\frac{3}{4}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
10. 如图，在 $▱$ ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE于G，BG= ，则梯形AECD的周长为（）

A、22 B、23 C、24 D、25

查看试题解析
11. 如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°，AB= $\frac{1}{2}$ BC=1，则下列结论：
①∠CAD=30° ②BD= $\sqrt{7}$ ③S_{平行四边形}_ABCD=AB•AC ④OE= $\frac{1}{4}$ AD ⑤S_△_APO= $\frac{\sqrt{3}}{12}$ ，正确的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

12. 已知一组数据：3，3，4，5，5，6，6，6. 这组数据的众数是．

查看试题解析
13. 若y= $\sqrt{x - 3} + \sqrt{3 - x} + 4$ ，则x+y= ．

查看试题解析
14. 若a为方程 $x^{2} - 3 x - 6 = 0$ 的一个根，则代数式 $a^{2} - 3 a + 7$ 的值是.

查看试题解析
15. 如图，某小区规划在一个长34m、宽22m的矩形ABCD上，修建三条同样宽的通道，使其中两条与AB平行，另一条与AD平行，其余部分种花草.要使每一块花草的面积都为100m² ，那么通道的宽应设计成m.

查看试题解析
16. 如图，已知△ABC的面积为24，点D在线段AC上，点D在线段BC的延长线上，且BF=4CF，四边形DCFE是平行四边形，则图中阴影部分的面积是.

查看试题解析

三、解答题

17. 计算

(1)、 $\sqrt{12} - 6 \sqrt{\frac{1}{3}} + \sqrt{48}$

(2)、 $(\sqrt{7} + \sqrt{3})(\sqrt{7} - \sqrt{3}) - \sqrt{16} + \sqrt{{(2 \sqrt{2} - 3)}^{2}}$

查看试题解析
18. 选用适当的方法解下列方程

(1)、2x²﹣5x﹣8＝0

(2)、（x﹣2）（2x﹣3）＝2（x﹣2）

查看试题解析
19. 如图，在所给的6×6方格中，每个小正方形的边长都是1.按要求画多边形，使它的各个顶点都在方格的顶点上.

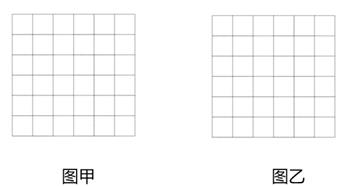(1)、在图甲中画一个面积为5的平行四边形.

(2)、在图乙中画一个平行四边形，使其有一个内角为45°.

查看试题解析
20. 某校八年级有800名学生，在一次跳绳模拟测试中，从中随机抽取部分学生，根据其测试成绩制作了下面两个统计图，请根据相关信息，解答下列问题：

(1)、本次抽取到的学生人数为，扇形统计图中 $m$ 的值为.

(2)、本次调查获取的样本数据的众数是（分），中位数是（分）.

(3)、根据样本数据，估计我校八年级模拟体测中得12分的学生约有多少人？

查看试题解析
21. 如图，在▱ ABCD 中，AE、BF 分别平分∠DAB 和∠ABC，交 CD 于点 E、F，AE、BF 相交于点 M．

(1)、求证：AE⊥BF；

(2)、判断线段 DF 与 CE 的大小关系，并予以证明．

查看试题解析
22. 某商场将每件进价为80元的某种商品原来按每件100出售，一天可售出100件，后来经过市场调查，发现这种商品每降低1元，其销量可增加10件．

(1)、求商场经营该商品原来一天可获利润多少元？

(2)、设后来该商品每件降价x元，若商场经营该商品一天要获利润2160元，则每件商品应降价多少元？

查看试题解析
23. 如图，在▱ABCD中，对角线AC，BD相交于点O，AB⊥AC，AB＝3cm，BC＝5cm.点P从A点出发沿AD方向匀速运动，速度为1cm/s.连接PO并延长交BC于点Q，设运动时间为t（0＜t＜5）.

(1)、当t为何值时，四边形ABQP是平行四边形？

(2)、设四边形OQCD的面积为y（cm²），求y与t之间的函数关系式；

(3)、是否存在某一时刻t，使点O在线段AP的垂直平分线上？若存在，求出t的值；若不存在，请说明理由.

查看试题解析