浙江省湖州市德清县2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2020-08-13 类型：期中考试

进入出卷网下载

一、单选题

1. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{\frac{1}{6}}$ B、 $\sqrt{0 .6}$ C、 $\sqrt{6}$ D、 $\sqrt{60}$

查看试题解析
2. 把一元二次方程x（x+1）＝3x+2化为一般形式，正确的是（）

A、x²+4x+3＝0 B、x²﹣2x+2＝0 C、x²﹣3x﹣1＝0 D、x²﹣2x﹣2＝0

查看试题解析
3. 甲乙两名同学本学期参加了相同的5次数学考试，老师想判断这两位同学的数学成绩谁更稳定，老师需比较这两人5次数学成绩的（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
4. 若正多边形的一个外角是 $60 °$ ，则该正多边形的内角和为（）

A、 $360 °$ B、 $540 °$ C、 $720 °$ D、 $900 °$

查看试题解析
5. 一个等腰三角形两边的长分别为 $5 \sqrt{2}$ 和 $2 \sqrt{3}$ ，则这个三角形的周长为（）.

A、 $10 \sqrt{2} + 2 \sqrt{3}$ B、 $5 \sqrt{2} + 4 \sqrt{3}$ C、 $10 \sqrt{2} + 2 \sqrt{3}$ 或 $5 \sqrt{2} + 4 \sqrt{3}$ D、 $10 \sqrt{2} + 4 \sqrt{3}$

查看试题解析
6. 在四边形ABCD中，对角线AC、BD交于点O，下列条件中，不能判定四边形ABCD是平行四边形的是（）

A、AB＝DC，AD＝BC B、AD∥BC，AD＝BC C、AB∥DC，AD＝BC D、OA＝OC，OD＝OB

查看试题解析
7. 如图，▱ABCD中，EF过对角线的交点O ， AB=4，AD=3，OF=1.3，则四边形BCEF的周长为（）

A、8.3 B、9.6 C、12.6 D、13.6

查看试题解析
8.
如图，在四边形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动，同时点Q从点B出发，以1个单位/s的速度沿BA向终点A运动．当四边形PQBC为平行四边形时，运动时间为（　　）

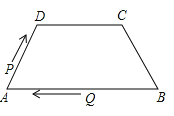A、4s B、3s C、2s D、1s

查看试题解析
9. 如图，在平面直角坐标系中，以O（0，0）、A（1，﹣1）、B（2，0）为顶点，构造平行四边形，下列各点中不能作为平行四边形第四个顶点坐标的是（）

A、（3，﹣1） B、（﹣1，﹣1） C、（1，1） D、（﹣2，﹣1）

查看试题解析
10. 设a、b为x²+x﹣2011=0的两个实根，则a³+a²+3a+2014b=（）

A、2014 B、﹣2014 C、2011 D、﹣2011

查看试题解析

二、填空题

11. 实数 $a$ 、 $b$ 在数轴上位置如图，化简： $| a + b | + \sqrt{{(a - b)}^{2}} =$ ；

查看试题解析
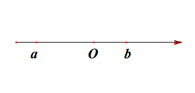12. 某市6月份日最高气温统计如图所示，则在日最高气温这组数据中，众数是℃，中位数是℃．

查看试题解析
13. 现要在一个长为40m，宽为26m的矩形花园中修建等宽的小道，剩余的地方种植花草.如图所示，要使种植花草的面积为864m² ，那么小道的宽度应是m．

查看试题解析
14. 如图，在▱ABCD中，AB＝3，BC＝5，以点B的圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心，以大于 $\frac{1}{2}$ PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为.

查看试题解析
15. 四边形具有不稳定性.如图，矩形 $A B C D$ 按箭头方向变形成平行四边形 $A' B' C' D'$ ，当变形后图形面积是原图形面积的一半时，则 $∠ A' =$ .

查看试题解析
16. 在 $△ A B C$ 中， $B C = a .$ 作BC边的三等分点 $C_{1}$ ，使得 $C C_{1}$ ： $B C_{1} = 1$ ：2，过点 $C_{1}$ 作AC的平行线交AB于点 $A_{1}$ ，过点 $A_{1}$ 作BC的平行线交AC于点 $D_{1}$ ，作 $B C_{1}$ 边的三等分点 $C_{2}$ ，使得 $C_{1} C_{2}$ ： $B C_{2} = 1$ ：2，过点 $C_{2}$ 作AC的平行线交AB于点 $A_{2}$ ，过点 $A_{2}$ 作BC的平行线交 $A_{1} C_{1}$ 于点 $D_{2}$ ；如此进行下去，则线段 $A_{n} D_{n}$ 的长度为.

查看试题解析

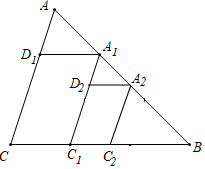
三、解答题

17. 计算：

(1)、 $\sqrt{12}$ + $\sqrt{32}$ ﹣6 $\sqrt{\frac{1}{2}}$ ；

(2)、已知x＝1﹣ $\sqrt{2}$ ，y＝1+ $\sqrt{2}$ ，求x²+y²﹣xy﹣2x+2y的值.

查看试题解析
18. 解方程：

(1)、 ${(x - 3)}^{2} + 2 x (x - 3) = 0$ ，

(2)、 $x^{2} - 4 x - 5 = 0$ .

查看试题解析
19. 平行四边形ABCD，AD=6，AB=8，点A的坐标为（-3，0），求B、C、D各点的坐标.

查看试题解析
20. 甲、乙两人分别在六次射击中的成绩如下表：（单位：环）
第1次
第2次
第3次
第4次
第5次
第6次
甲
6
7
7
8
6
8
乙
5
9
6
8
5
9
分别算出两人射击的平均数和方差．这六次射击中成绩发挥比较稳定的是谁？

查看试题解析
21. 已知关于x的一元二次方程（x﹣k）²﹣2x+2k＝0有两个实数根x₁、x₂.

(1)、求实数k的取值范围；

(2)、当实数k为何值时，代数式x₁²+x₂²﹣x₁•x₂+1取得最小值，并求出该最小值.

查看试题解析
22. 如图，四边形ABCD中，AC，BD相交于点O，O是AC的中点，AD∥BC.

(1)、求证：四边形ABCD是平行四边形

(2)、若AC⊥BD，且AB=4，则四边形ABCD的周长为.

查看试题解析
23. 某商场在去年底以每件80元的进价购进一批同型号的服装，一月份以每件150元的售价销售了320件，二、三月份该服装畅销，销量持续走高，在售价不变的情况下，三月底统计知三月份的销量达到了500件

(1)、求二、三月份服装销售量的平均月增长率

(2)、从四月份起商场因换季清仓采用降价促销的方式，经调查发现，在三月份销量的基础上，该服装售价每降价5元，月销售量增加10件，当每件降价多少元时，四月份可获利12000元?

查看试题解析
24. 在平面直角坐标系xOy中，O为坐标原点，四边形OABC的顶点A在x轴的正半轴上，OA=4，OC=2，点P，点Q分别是边BC，边AB上的点，连结AC，PQ，点B₁是点B关于PQ的对称点.

(1)、若四边形OABC为长方形，如图1，
①求点B的坐标；

②若BQ=BP，且点B₁落在AC上，求点B₁的坐标；

(2)、若四边形OABC为平行四边形，如图2，且OC⊥AC，过点B₁作B₁F∥x轴，与对角线AC，边OC分别交于点E，点F.若B₁E：B₁F=1：3，点B₁的横坐标为m，求点B₁的纵坐标（用含m的代数式表示）.

查看试题解析

	第1次	第2次	第3次	第4次	第5次	第6次
甲	6	7	7	8	6	8
乙	5	9	6	8	5	9