江苏省泰州市姜堰区2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-08-13 类型:期中考试
一、单选题
-
1. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列分式中,属于最简分式的是( )A、 B、 C、 D、3. 下列事件中,属于必然事件的是( )A、打开电视机,它正在播广告 B、买一张电影票,座位号是偶数 C、抛掷一枚质地均匀的骰子,6点朝上 D、若 是实数,则4. 为了了解天鹅湖校区2019-2020学年1600名七年级学生的体重情况,从中抽取了100名学生的体重,就这个问题,下面说法正确的是( )A、1600名学生的体重是总体 B、1600名学生是总体 C、每个学生是个体 D、100名学生是所抽取的一个样本5. 已知四边形ABCD的对角线AC、BD互相垂直,且AC=10,BD=8,那么顺次连接四边形ABCD各边中点所得到的四边形面积为( )A、40 B、20 C、16 D、86. 如图,平行四边形ABCD的对角线AC、BD交于点O,AE平分 交BC于点E,且 , ,连接OE.下列结论:① ;② ;③ ;④ ,成立的个数有( )
2. 下列分式中,属于最简分式的是( )A、 B、 C、 D、3. 下列事件中,属于必然事件的是( )A、打开电视机,它正在播广告 B、买一张电影票,座位号是偶数 C、抛掷一枚质地均匀的骰子,6点朝上 D、若 是实数,则4. 为了了解天鹅湖校区2019-2020学年1600名七年级学生的体重情况,从中抽取了100名学生的体重,就这个问题,下面说法正确的是( )A、1600名学生的体重是总体 B、1600名学生是总体 C、每个学生是个体 D、100名学生是所抽取的一个样本5. 已知四边形ABCD的对角线AC、BD互相垂直,且AC=10,BD=8,那么顺次连接四边形ABCD各边中点所得到的四边形面积为( )A、40 B、20 C、16 D、86. 如图,平行四边形ABCD的对角线AC、BD交于点O,AE平分 交BC于点E,且 , ,连接OE.下列结论:① ;② ;③ ;④ ,成立的个数有( )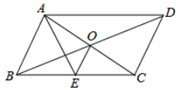 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
7. 如果分式 有意义,那么x的取值范围是 .8. 在一个不透明的布袋中,有红球、白球共20个,除颜色外其他完全相同,小明通过多次摸球试验后发现,其中摸到红球的频率稳定在50%,则随机从口袋中摸出一个是红球的概率是 .9. 若 ,则 .10. 货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少.设货车的速度为x千米/小时,依题意可列方程 .11. 已知以三角形各边中点为顶点的三角形的周长为6cm,则原三角形的周长为cm.12. 如图,四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点.请你添加一个条件,使四边形EFGH为矩形,应添加的条件是 .
 13. 如图,将▱ABCD沿对角线BD折叠,使点C落在点C'处,若∠1=∠2=50°,则∠C= .
13. 如图,将▱ABCD沿对角线BD折叠,使点C落在点C'处,若∠1=∠2=50°,则∠C= .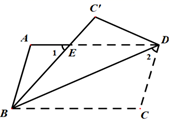 14. 若 ,那么 .15. 如图,在Rt△ABC中,∠B=90°,AC=5,BC=4,点D在线段BC上一动点,以AC为对角线的 中,则DE的最小值是 .
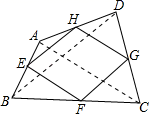
14. 若 ,那么 .15. 如图,在Rt△ABC中,∠B=90°,AC=5,BC=4,点D在线段BC上一动点,以AC为对角线的 中,则DE的最小值是 .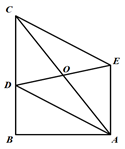 16. 如图,点E、F分别在平行四边形ABCD边BC和AD上(E、F都不与两端点重合),连结AE、DE、BF、CF,其中AE和BF交于点G,DE和CF交于点H.令 , .若 ,且S▱ABCD=36,则四边形FGEH的面积为 .
16. 如图,点E、F分别在平行四边形ABCD边BC和AD上(E、F都不与两端点重合),连结AE、DE、BF、CF,其中AE和BF交于点G,DE和CF交于点H.令 , .若 ,且S▱ABCD=36,则四边形FGEH的面积为 .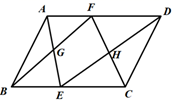
三、解答题
-
17.(1)、计算: ;(2)、解方程: .18. 先化简,再求值: 其中19. 已知△ABC的顶点A、B、C在边长为1的网格格点上.
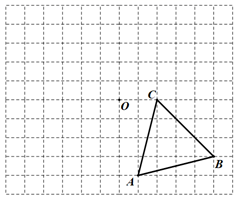 (1)、①画△ABC绕点O逆时针旋转90°得到的△A1B1C1;
(1)、①画△ABC绕点O逆时针旋转90°得到的△A1B1C1;②画△A1B1C1关于点O的中心对称图形△A2B2C2;
(2)、平行四边形A1B1A2B2的面积为 .20. 中华文明,源远流长,中华汉字,寓意深广。为了传承优秀传统文化,某校团委组织了一次全校1500名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了部分学生的成绩作为样本进行整理,得到下列不完整的统计图表.请你根据表中提供的信息,解答下列问题: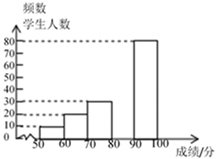
成绩x/分
频数
频率
50≤x<60
10
0.05
60≤x<70
20
0.10
70≤x<80
30
b
80≤x<90
a
0.30
90≤x≤100
80
0.40
(1)、此次调查的样本容量为;(2)、在表中: = , =;(3)、补全频数分布直方图;(4)、若成绩在80分以上(包括80分)的为“A”级,则该校参加这次比赛的1500名学生中,成绩为“A”级的约有多少人?21. 已知关于x的分式方程 ,(1)、若分式方程有增根,求m的值;(2)、若分式方程的解是正数,求m的取值范围.22. 在“为疫情灾区武汉捐款”献爱心的活动中,甲、乙两公司各捐款60000元,已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐40元.问:甲、乙两公司各有多少人?23. 如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.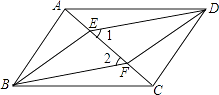 (1)、求证:AE=CF;(2)、求证:四边形EBFD是平行四边形.24. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE//AC,且DE:AC=1:2,连接CE、OE,连接AE交OD于点F.
(1)、求证:AE=CF;(2)、求证:四边形EBFD是平行四边形.24. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE//AC,且DE:AC=1:2,连接CE、OE,连接AE交OD于点F.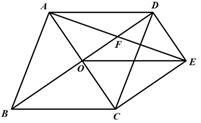 (1)、求证:OE=CD;(2)、若菱形ABCD的边长为2,∠ABC=60°,求AE的长.25. 在矩形纸片ABCD中,AB=6,BC=8,
(1)、求证:OE=CD;(2)、若菱形ABCD的边长为2,∠ABC=60°,求AE的长.25. 在矩形纸片ABCD中,AB=6,BC=8,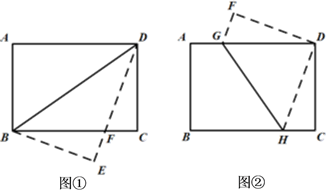 (1)、将矩形纸片沿BD折叠,点A落在点E处(如图①),设DE与BC相交于点F,试说明△DBF是等腰三角形,并求出其周长.(2)、将矩形纸片折叠,使点B与点D重合(如图②),求折痕GH的长.26. 如图,在平面直角坐标系xOy中,直线 分别交x轴,y轴于A、B两点,点A关于原点O的对称点为点D,点C在第一象限,且四边形ABCD为平行四边形.
(1)、将矩形纸片沿BD折叠,点A落在点E处(如图①),设DE与BC相交于点F,试说明△DBF是等腰三角形,并求出其周长.(2)、将矩形纸片折叠,使点B与点D重合(如图②),求折痕GH的长.26. 如图,在平面直角坐标系xOy中,直线 分别交x轴,y轴于A、B两点,点A关于原点O的对称点为点D,点C在第一象限,且四边形ABCD为平行四边形.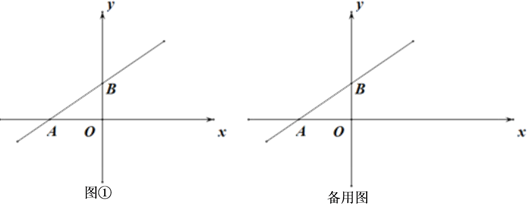 (1)、在图①中,画出平行四边形ABCD,并直接写出C、D两点的坐标;(2)、动点P从点C出发,沿线段CB以每秒1个单位的速度向终点B运动;同时,动点Q从点A出发,沿线段AD以每秒1个单位的速度向终点D运动,设点P运动的时间为t秒.
(1)、在图①中,画出平行四边形ABCD,并直接写出C、D两点的坐标;(2)、动点P从点C出发,沿线段CB以每秒1个单位的速度向终点B运动;同时,动点Q从点A出发,沿线段AD以每秒1个单位的速度向终点D运动,设点P运动的时间为t秒.①若△POQ的面积为3,求t的值;
②点O关于B点的对称点为M,点C关于x轴的对称点为N,过点P作PH⊥x轴,问MP+PH+NH是否有最小值,如果有求出相应的点P的坐标;如果没有,请说明理由.