湖北省武汉市汉阳区2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2020-08-13 类型：期中考试

进入出卷网下载

一、单选题

1. 函数 $y = \sqrt{2 x + 1}$ 中的自变量 $x$ 的取值范围是（）

A、 $x \neq - \frac{1}{2}$ B、 $x \geq - 1$ C、 $x > - \frac{1}{2}$ D、 $x ⩾ - \frac{1}{2}$

查看试题解析
2. 下列各组中的三条线段，能构成直角三角形的是（）

A、7，20，24 B、4，5，6 C、 $\sqrt{3}, \sqrt{4}, \sqrt{5}$ D、3，4，5

查看试题解析
3. 下列各式成立的是（）

A、 $3 \sqrt{2} - \sqrt{2} = 3$ B、 $\sqrt{2 + \frac{2}{3}} = 2 \sqrt{\frac{2}{3}}$ C、 $\frac{\sqrt{18} - \sqrt{8}}{2} = \sqrt{9} - \sqrt{4} = 1$ D、 $\sqrt{18} - \sqrt{\frac{2}{9}} = \frac{7}{3} \sqrt{2}$

查看试题解析
4. 如图，公路 $A C$ ， $B C$ 互相垂直，公路 $A B$ 的中点 $M$ 与点 $C$ 被湖隔开.测得 $A B$ 的长为 $1.6 k m$ ，则 $M ， C$ 两点间的距离为（）

A、 $0.5 k m$ B、 $0.6 k m$ C、 $0.8 k m$ D、 $1.2 k m$

查看试题解析
5. 如图，若平行四边形 $A B C O$ 的顶点 $O ， A ， C$ 的坐标分别是 $(0 ， 0) ， (6 ， 0) ， (3 ， 4)$ ，则顶点 $B$ 的坐标是（）

A、 $(9 ， 4)$ B、 $(6 ， 4)$ C、 $(4 ， 9)$ D、 $(8 ， 4)$

查看试题解析
6. 如图，菱形 $A B C D$ 的对角线 $A C ， B D$ 交于点 $O$ ， $A C = 2$ ， $B D = 8$ ，将 $△ A B O$ 沿点 $A$ 到点 $C$ 的方向平移，得到 $△ A^{'} B^{'} O^{'}$ ，当点 $A^{'}$ 与点 $C$ 重合时，点 $A$ 与点 $B^{'}$ 之间的距离为（）

A、3 B、4 C、5 D、6

查看试题解析
7. 如图，在平行四边形 $A B C D$ 中， $E$ 为边 $C D$ 上一点，将 $△ A D E$ 沿 $A E$ 折叠至 $△ A D^{'} E$ 处， $A D^{'}$ 与 $C E$ 交于点 $F$ .若 $∠ B = 54 °$ ， $∠ D A E = 20 °$ ，则 $∠ F E D^{'}$ 的大小为（）

A、27° B、32° C、36° D、40°

查看试题解析
8. 正方形ABCD的边AB上有一动点E，以EC为边作矩形ECFG，且边FG过点D，在点E从点A移动到点B的过程中，矩形ECFG的面积（）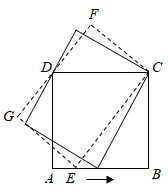

A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变

查看试题解析
9. 如图，平面内某正方形内有一长为10宽为5的矩形，它可以在该正方形的内部及边界通过平移或旋转的方式，自由地从横放变换到竖放，则该正方形边长的最小整数 $n$ 为（）

A、10 B、11 C、12 D、13

查看试题解析
10. 如图，正方形 $A B C D$ 中，延长 $C B$ 至 $E$ 使 $C B = 2 E B$ ，以 $E B$ 为边作正方形 $E F G B$ ，延长 $F G$ 交 $D C$ 于 $M$ ，连接 $A M$ ， $A F$ ， $H$ 为 $A D$ 的中点，连接 $F H$ 分别与 $A B$ ， $A M$ 交于点 $N ， K$ .则下列说法：① $△ A N H ≌ △ G N F$ ；② $∠ D A M = ∠ N F G$ ；③ $F N = 2 N K$ ；④ $S_{△ A F N} ： S_{四边形 D M K H} = 2 ： 7$ .其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 已知四边形 $A B C D$ 是周长为32的平行四边形，若 $A B = 6$ ，则 $B C =$ .

查看试题解析
12. 若 $x = \sqrt{3} + 1, y = \sqrt{3} - 1$ ，则 ${(x + y)}^{2} =$ .

查看试题解析
13. 如图，在菱形 $A B C D$ 中， $M$ ， $N$ 分别在 $A B$ ， $C D$ 上，且 $A M = C N$ ， $M N$ 与 $A C$ 交于点 $O$ ，连接 $B O$ .若 $∠ D A C = 26 °$ ，则 $∠ O B C$ 的大小为.

查看试题解析
14. 观察下列各式：
$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1 \times 2} = 1 + (1 - \frac{1}{2})$ ；

$\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2 \times 3} = 1 + (\frac{1}{2} - \frac{1}{3})$ ；

$\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3 \times 4} = 1 + (\frac{1}{3} - \frac{1}{4})$ ；

……

请利用你发现的规律，计算 $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + \sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} + \dots + \sqrt{1^{2} + \frac{1}{2019^{2}} + \frac{1}{2020^{2}}}$ ，其结果为.

查看试题解析
15. 如图所示，以 $R t △ A B C$ 的斜边 $B C$ 为边，在 $△ A B C$ 的同侧作正方形 $B C E F$ ， $B E$ ， $C F$ 交于点 $O$ ，连接 $A O$ .若 $A B = 4$ ， $A O = 4 \sqrt{2}$ ，则 $B C =$ .

查看试题解析
16. 如图，一副三角板 $A B C$ 和 $E D F$ 拼合在一起，边 $A C$ 与 $E F$ 重合， $∠ B A C = 30 °$ ， $∠ D A C = 45 °$ ， $∠ A D C = ∠ A C B = 90 °$ ， $A C = 6 c m$ .当点 $E$ 从点 $A$ 出发沿 $A C$ 向下滑动时，点 $F$ 同时从点 $C$ 出发沿射线 $B C$ 向右滑动.当点 $E$ 从点 $A$ 滑动到点 $C$ 时，连接 $B D$ ，则 $△ B C D$ 的面积最大值为 $c m^{2}$ .

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{27} \times \sqrt{50} \div 2 \sqrt{6}$ ；

(2)、 $2 \sqrt{12} - 6 \sqrt{\frac{1}{3}} + 3 \sqrt{48}$ .

查看试题解析
18. 如图，在平行四边形 $A B C D$ 中， $A H ⊥ B D$ 于 $H$ ， $C G ⊥ B D$ 于 $G$ ，连接 $C H$ 和 $A G$ ，求证： $∠ C H G = ∠ A G H$ .

查看试题解析
19. 如图，在笔直的铁路上 $A ， B$ 两点相距 $20 k m$ ， $C ， D$ 为两村庄， $D A = 8 k m$ ， $C B = 14 k m$ ， $D A ⊥ A B$ 于 $A$ ， $C B ⊥ A B$ 于 $B$ .现要在 $A B$ 上建一个中转站 $E$ ，使得 $C$ ， $D$ 两村到 $E$ 站的距离相等，求 $A E$ 的长.

查看试题解析
20. 如图，在菱形 $A B C D$ 中， $A B = 6$ ， $∠ D A B = 60 °$ ，点 $E$ 是 $A D$ 边的中点，点 $M$ 是 $A B$ 边上一动点（不与点 $A$ 重合），延长 $M E$ 交射线 $C D$ 于点 $N$ ，连接 $M D$ ， $A N$ .

(1)、求证：四边形 $A M D N$ 是平行四边形；

(2)、填空：
①当 $A M$ 的值为时，四边形 $A M D N$ 是矩形；

②当 $A M$ 的值为时，四边形 $A M D N$ 是菱形.

查看试题解析
21. 如图，在每个小正方形的边长均为1的网格中，点 $A ， B ， C ， D$ 均在格点上，请在此网格中仅用无刻度的直尺画图（保留连线痕迹）.

（1）画出线段 $B E$ ，使 $B E ∥ A C$ ，且 $B E = A C$ ；
（2）画出以 $A C$ 为边的正方形 $A C M N$ ；
（3）在（1）的条件下，画出直线 $P Q$ ，使 $P Q$ 平分四边形 $A B E D$ 的面积（作出一条即可）.

查看试题解析
22. 阅读材料，请回答下列问题.
材料一：我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”，即已知三角形的三边长，求它的面积，用现代式子表示即为： $S = \sqrt{\frac{1}{4} [a^{2} b^{2} - {(\frac{a^{2} + b^{2} - c^{2}}{2})}^{2}]}$ ①（其中 $a ， b ， c$ 为三角形的三边长， $S$ 为面积），而另一个文明古国古希腊也有求三角形面积的“海伦公式”； $S = \sqrt{p (p - a) (p - b) (p - c)}$ ……②（其中 $p = \frac{a + b + c}{2}$ ）

材料二：对于平方差公式： $a^{2} - b^{2} = (a + b) (a - b)$ 公式逆用可得： $(a + b) (a - b) = a^{2} - b^{2}$ ，例： $a^{2} - {(b + c)}^{2} = (a + b + c) (a - b - c)$

(1)、若已知三角形的三边长分别为4，5，7，请分别运用公式①和公式②，计算该三角形的面积；

(2)、你能否由公式①推导出公式②？请试试，写出推导过程.

查看试题解析
23.

(1)、如图①，正方形 $A E F G$ 的两边分别在正方形 $A B C D$ 的边 $A B$ 和 $A D$ 上，连接 $C F$ .填空：线段 $D G$ 与 $C F$ 的数量关系为；直线 $D G$ 与 $C F$ 所夹锐角的大小为.

(2)、如图②，将正方形 $A E F G$ 绕点 $A$ 顺时针旋转，在旋转的过程中，（1）中的结论是否仍然成立，请说明理由.

(3)、把图②中的正方形都换成菱形，且 $∠ B A D = ∠ G A E = 60 °$ ，如图③，直接写出 $D G ： C F =$ .

查看试题解析
24. 如图1，在矩形 $A B C D$ 中， $A B = a$ ， $B C = 3$ ，动点 $P$ 从 $B$ 出发，以每秒1个单位的速度沿射线 $B C$ 方向移动，作 $△ P A B$ 关于直线 $P A$ 的对称 $△ P A B^{'}$ ，设点 $P$ 的运动时间为 $t (s)$ .

(1)、当 $a = 4$ 时.
①如图2.当点 $B^{'}$ 落在 $A C$ 上时，显然 $△ P C B^{'}$ 是直角三角形，求此时 $t$ 的值；

②当点 $B^{'}$ 不落在 $A C$ 上时，请直接写出 $△ P C B^{'}$ 是直角三角形时 $t$ 的值；

(2)、若直线 $P B^{'}$ 与直线 $C D$ 相交于点 $M$ ，且当 $t < 3$ 时， $∠ P A M = 45 °$ .问：当 $t > 3$ 时， $∠ P A M$ 的大小是否发生变化，若不变，请说明理由.

查看试题解析