四川省宜宾市2020年中考数学试卷
试卷更新日期:2020-08-12 类型:中考真卷
一、单选题
-
1. 6的相反数为( )A、-6 B、6 C、 D、2. 我国自主研发的北斗系统技术世界领先,2020年6月23日在西昌卫星发射中心成功发射最后一颗北斗三号组网卫星,该卫星发射升空的速度是7100米/秒,将7100用科学记数法表示为( )A、7100 B、 C、 D、3. 如图所示,圆柱的主视图是( )
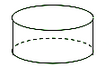 A、
A、 B、
B、 C、
C、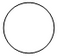 D、
D、 4. 计算正确的是( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示正确的是( )A、
4. 计算正确的是( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、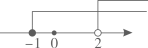 D、
D、 6. 7名学生的鞋号(单位:厘米)由小到大是:20,21,22,22,23,23,则这组数据的众数和中位数分别是( )A、20,21 B、21,22 C、22,22 D、22,237. 如图,M,N分别是 的边AB,AC的中点,若 ,则 =( )
6. 7名学生的鞋号(单位:厘米)由小到大是:20,21,22,22,23,23,则这组数据的众数和中位数分别是( )A、20,21 B、21,22 C、22,22 D、22,237. 如图,M,N分别是 的边AB,AC的中点,若 ,则 =( )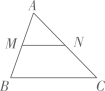 A、 B、 C、 D、8. 学校为了丰富学生的知识,需要购买一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多8元,已知学校用15000元购买科普类图书的本数与用12000元购买文学书的本数相等,设文学类图书平均每本x元,则列方程正确的是( )A、 B、 C、 D、9. 如图,AB是 的直径,点C是圆上一点,连结AC和BC,过点C作 于D,且 ,则 的周长为( )
A、 B、 C、 D、8. 学校为了丰富学生的知识,需要购买一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多8元,已知学校用15000元购买科普类图书的本数与用12000元购买文学书的本数相等,设文学类图书平均每本x元,则列方程正确的是( )A、 B、 C、 D、9. 如图,AB是 的直径,点C是圆上一点,连结AC和BC,过点C作 于D,且 ,则 的周长为( )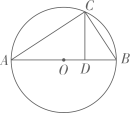 A、 B、 C、 D、10. 某单位为响应政府号召,需要购买分类垃圾桶6个,市场上有A型和B型两种分类垃圾桶,A型分类垃圾桶500元/个,B型分类垃圾桶550元/个,总费用不超过3100元,则不同的购买方式有( )A、2种 B、3种 C、4种 D、5种11. 如图, 都是等边三角形,且B,C,D在一条直线上,连结 ,点M,N分别是线段BE,AD上的两点,且 ,则 的形状是( )
A、 B、 C、 D、10. 某单位为响应政府号召,需要购买分类垃圾桶6个,市场上有A型和B型两种分类垃圾桶,A型分类垃圾桶500元/个,B型分类垃圾桶550元/个,总费用不超过3100元,则不同的购买方式有( )A、2种 B、3种 C、4种 D、5种11. 如图, 都是等边三角形,且B,C,D在一条直线上,连结 ,点M,N分别是线段BE,AD上的两点,且 ,则 的形状是( )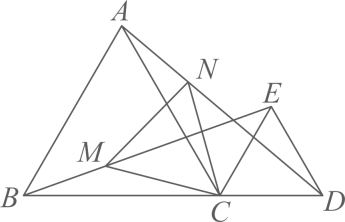 A、等腰三角形 B、直角三角形 C、等边三角形 D、不等边三角形12. 函数 的图象与x轴交于点(2,0),顶点坐标为(-1,n),其中 ,以下结论正确的是( )
A、等腰三角形 B、直角三角形 C、等边三角形 D、不等边三角形12. 函数 的图象与x轴交于点(2,0),顶点坐标为(-1,n),其中 ,以下结论正确的是( )① ;
②函数 在 处的函数值相等;
③函数 的图象与的函数 图象总有两个不同的交点;
④函数 在 内既有最大值又有最小值.
A、①③ B、①②③ C、①④ D、②③④二、填空题
-
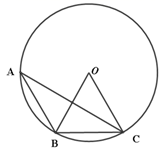
13. 分解因式: .14. 如图,A,B,C是 上的三点,若 是等边三角形,则 .
 15. 一元二次方程 的两根为 ,则16. 如图,四边形 中, 是AB上一动点,则 的最小值是
15. 一元二次方程 的两根为 ,则16. 如图,四边形 中, 是AB上一动点,则 的最小值是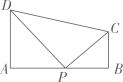 17. 定义:分数 (m,n为正整数且互为质数)的连分数(其中为整数,且等式右边的每一个分数的分子都为1),记作 :例如 , 的连分数是 ,记作 ,则 .18. 在直角三角形ABC中, 是AB的中点,BE平分 交AC于点E连接CD交BE于点O,若 ,则OE的长是 .
17. 定义:分数 (m,n为正整数且互为质数)的连分数(其中为整数,且等式右边的每一个分数的分子都为1),记作 :例如 , 的连分数是 ,记作 ,则 .18. 在直角三角形ABC中, 是AB的中点,BE平分 交AC于点E连接CD交BE于点O,若 ,则OE的长是 .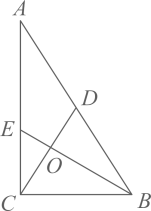
三、解答题
-
19.(1)、计算:(2)、化简:20. 如图,在三角形ABC中,点D是BC上的中点,连接AD并延长到点E,使 ,连接CE.
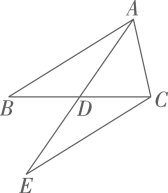 (1)、求证:(2)、若 的面积为5,求 的面积.21. 在疫情期间,为落实停课不停学,某校对本校学生某一学科在家学习的情况进行抽样调查,了解到学生的学习方式有:电视直播、任教老师在线辅导、教育机构远程教学、自主学习,参入调查的学生只能选择一种学习方式,将调查结果绘制成不完整的扇形统计图和条形统计图,解答下列问题.
(1)、求证:(2)、若 的面积为5,求 的面积.21. 在疫情期间,为落实停课不停学,某校对本校学生某一学科在家学习的情况进行抽样调查,了解到学生的学习方式有:电视直播、任教老师在线辅导、教育机构远程教学、自主学习,参入调查的学生只能选择一种学习方式,将调查结果绘制成不完整的扇形统计图和条形统计图,解答下列问题.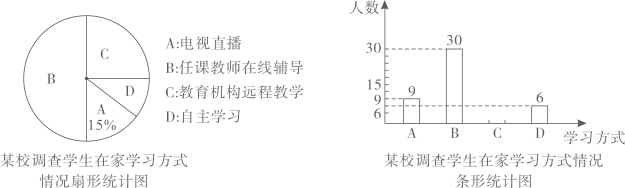 (1)、本次受调查的学生有人;(2)、补全条形统计图;(3)、根据调查结果,若本校有1800名学生,估计有多少名学生与任课教师在线辅导?22. 如图, 两楼地面距离BC为 米,楼AB高30米,从楼AB的顶部点A测得楼CD顶部点D的仰角为45度.
(1)、本次受调查的学生有人;(2)、补全条形统计图;(3)、根据调查结果,若本校有1800名学生,估计有多少名学生与任课教师在线辅导?22. 如图, 两楼地面距离BC为 米,楼AB高30米,从楼AB的顶部点A测得楼CD顶部点D的仰角为45度.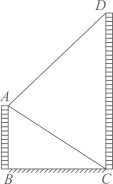 (1)、求 的大小;(2)、求楼CD的高度(结果保留根号).23. 如图,一次函数 的图像与反比例函数 的图像交于 两点,过点A作 于点C.
(1)、求 的大小;(2)、求楼CD的高度(结果保留根号).23. 如图,一次函数 的图像与反比例函数 的图像交于 两点,过点A作 于点C. (1)、求一次函数和反比例函数的表达式;(2)、求四边形ABOC的面积.24. 如图,已知AB是圆O的直径,点C是圆上异于A,B的一点,连接BC并延长至点D,使得 ,连接AD交 于点E,连接BE.
(1)、求一次函数和反比例函数的表达式;(2)、求四边形ABOC的面积.24. 如图,已知AB是圆O的直径,点C是圆上异于A,B的一点,连接BC并延长至点D,使得 ,连接AD交 于点E,连接BE.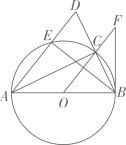 (1)、求证: 是等腰三角形;(2)、连接OC并延长,与B以为切点的切线交于点F,若 ,求 的长.25. 如图,已知二次函数图象的顶点在原点,且点(2,1)在二次函数的图象上,过点F(0,1)作x轴的平行线交二次函数的图象于M,N两点
(1)、求证: 是等腰三角形;(2)、连接OC并延长,与B以为切点的切线交于点F,若 ,求 的长.25. 如图,已知二次函数图象的顶点在原点,且点(2,1)在二次函数的图象上,过点F(0,1)作x轴的平行线交二次函数的图象于M,N两点 (1)、求二次函数的表达式;(2)、P为平面内一点,当 时等边三角形时,求点P的坐标;(3)、在二次函数的图象上是否存在一点E,使得以点E为圆心的圆过点F和和点N,且与直线 相切,若存在,求出点E的坐标,并求 的半径;若不存在,说明理由.
(1)、求二次函数的表达式;(2)、P为平面内一点,当 时等边三角形时,求点P的坐标;(3)、在二次函数的图象上是否存在一点E,使得以点E为圆心的圆过点F和和点N,且与直线 相切,若存在,求出点E的坐标,并求 的半径;若不存在,说明理由.