上海市2020年中考数学试卷

试卷更新日期：2020-08-12 类型：中考真卷

进入出卷网下载

一、单选题

1. 下列各式中与 $\sqrt{3}$ 是同类二次根式的是（）

A、 $\sqrt{6}$ B、 $\sqrt{9}$ C、 $\sqrt{12}$ D、 $\sqrt{18}$

查看试题解析
2. 用换元法解方程 $\frac{x + 1}{x^{2}}$ + $\frac{x^{2}}{x + 1}$ =2时，若设 $\frac{x + 1}{x^{2}}$ =y ，则原方程可化为关于y的方程是（）

A、y²﹣2y+1=0 B、y²+2y+1=0 C、y²+y+2=0 D、y²+y﹣2=0

查看试题解析
3. 我们经常将调查、收集得来的数据用各类统计图进行整理与表示．下列统计图中，能凸显由数据所表现出来的部分与整体的关系的是（）

A、条形图 B、扇形图 C、折线图 D、频数分布直方图

查看试题解析
4. 已知反比例函数的图象经过点(2，﹣4)，那么这个反比例函数的解析式是（）

A、y= $\frac{2}{x}$ B、y=﹣ $\frac{2}{x}$ C、y= $\frac{8}{x}$ D、y=﹣ $\frac{8}{x}$

查看试题解析
5. 下列命题中，真命题是（）

A、对角线互相垂直的梯形是等腰梯形 B、对角线互相垂直的平行四边形是正方形 C、对角线平分一组对角的平行四边形是菱形 D、对角线平分一组对角的梯形是直角梯形

查看试题解析
6. 如果存在一条线把一个图形分割成两个部分，使其中一个部分沿某个方向平移后能与另一个部分重合，那么我们把这个图形叫做平移重合图形．下列图形中，平移重合图形是（）

A、平行四边形 B、等腰梯形 C、正六边形 D、圆

查看试题解析

二、填空题

7. 计算： $2 a \cdot 3 a b =$ .

查看试题解析
8. 已知f(x)= $\frac{2}{x - 1}$ ，那么f(3)的值是．

查看试题解析
9. 如果函数y＝kx（k≠0）的图象经过第二、四象限，那么y的值随x的值增大而．（填“增大”或“减小”）

查看试题解析
10. 如果关于x的方程x²﹣4x+m=0有两个相等的实数根，那么m的值是．

查看试题解析
11. 如果从1，2，3，4，5，6，7，8，9，10这10个数中任意选取一个数，那么取到的数恰好是5的倍数的概率是．

查看试题解析
12. 如果将抛物线y=x²向上平移3个单位，那么所得新抛物线的表达式是．

查看试题解析
13. 为了解某区六年级8400名学生中会游泳的学生人数，随机调查了其中400名学生，结果有150名学生会游泳，那么估计该区会游泳的六年级学生人数约为．

查看试题解析
14. 《九章算术》中记载了一种测量井深的方法．如图所示，在井口B处立一根垂直于井口的木杆BD ，从木杆的顶端D观察井水水岸C ，视线DC与井口的直径AB交于点E ，如果测得AB=1.6米，BD=1米，BE=0.2米，那么井深AC为米．

查看试题解析
15. 如图，AC、BD是平行四边形ABCD的对角线，设 $\vec{B C}$ = $\vec{a}$ ， $\vec{C A}$ = $\vec{b}$ ，那么向量 $\vec{B D}$ 用向量 $\vec{a} ， \vec{b}$ 表示为．

查看试题解析
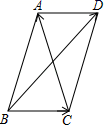16. 小明从家步行到学校需走的路程为1800米．图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系，根据图象提供的信息，当小明从家出发去学校步行15分钟时，到学校还需步行米．

查看试题解析
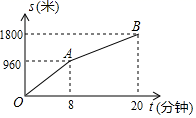17. 如图，在△ABC中，AB=4，BC=7，∠B=60°，点D在边BC上，CD=3，联结AD ．如果将△ACD沿直线AD翻折后，点C的对应点为点E ，那么点E到直线BD的距离为．

查看试题解析
18. 在矩形ABCD中，AB=6，BC=8，点O在对角线AC上，圆O的半径为2，如果圆O与矩形ABCD的各边都没有公共点，那么线段AO长的取值范围是．

查看试题解析

三、解答题

19. 计算： $27^{\frac{1}{3}}$ + $\frac{1}{\sqrt{5} + 2}$ ﹣( $\frac{1}{2}$ )^﹣2+|3﹣ $\sqrt{5}$ |．

查看试题解析
20. 解不等式组： ${\begin{array}{l} 10 x > 7 x + 6 \\ x - 1 < \frac{x + 7}{3} \end{array}$

查看试题解析
21. 如图，在直角梯形ABCD中， $A B // D C$ ，∠DAB=90°，AB=8，CD=5，BC=3 $\sqrt{5}$ ．

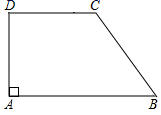(1)、求梯形ABCD的面积；

(2)、联结BD ，求∠DBC的正切值．

查看试题解析
22. 去年某商店“十一黄金周”进行促销活动期间，前六天的总营业额为450万元，第七天的营业额是前六天总营业额的12%．

(1)、求该商店去年“十一黄金周”这七天的总营业额；

(2)、去年，该商店7月份的营业额为350万元，8、9月份营业额的月增长率相同，“十一黄金周”这七天的总营业额与9月份的营业额相等．求该商店去年8、9月份营业额的月增长率．

查看试题解析
23. 已知：如图，在菱形ABCD中，点E、F分别在边AB、AD上，BE=DF ， CE的延长线交DA的延长线于点G ， CF的延长线交BA的延长线于点H ．

(1)、求证：△BEC∽△BCH；

(2)、如果BE²=AB•AE ，求证：AG=DF ．

查看试题解析
24. 在平面直角坐标系xOy中，直线y=﹣ $\frac{1}{2}$ x+5与x轴、y轴分别交于点A、B(如图)．抛物线y=ax²+bx(a≠0)经过点A ．

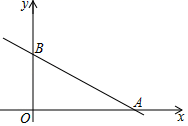(1)、求线段AB的长；

(2)、如果抛物线y=ax²+bx经过线段AB上的另一点C ，且BC= $\sqrt{5}$ ，求这条抛物线的表达式；

(3)、如果抛物线y=ax²+bx的顶点D位于△AOB内，求a的取值范围．

查看试题解析
25. 如图，△ABC中，AB=AC ， ⊙O是△ABC的外接圆，BO的延长交边AC于点D ．

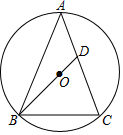(1)、求证：∠BAC=2∠ABD；

(2)、当△BCD是等腰三角形时，求∠BCD的大小；

(3)、当AD=2，CD=3时，求边BC的长．

查看试题解析