山西省2020年中考数学试卷
试卷更新日期:2020-08-12 类型:中考真卷
一、单选题
-
1. 计算 的结果是( )A、 B、 C、 D、2. 自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识.下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 下列几何体都是由4个大小相同的小正方体组成的,其中主视图与左视图相同的几何体是( )A、
3. 下列运算正确的是( )A、 B、 C、 D、4. 下列几何体都是由4个大小相同的小正方体组成的,其中主视图与左视图相同的几何体是( )A、 B、
B、 C、
C、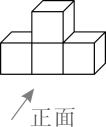 D、
D、 5. 泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的( )
5. 泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的( ) A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似6. 不等式组 的解集是( )A、 B、 C、 D、7. 已知点 , , 都在反比例函数 的图像上,且 ,则 , , 的大小关系是( )A、 B、 C、 D、8. 中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到 , , 两点之间的距离为 ,圆心角为 ,则图中摆盘的面积是( )
A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似6. 不等式组 的解集是( )A、 B、 C、 D、7. 已知点 , , 都在反比例函数 的图像上,且 ,则 , , 的大小关系是( )A、 B、 C、 D、8. 中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到 , , 两点之间的距离为 ,圆心角为 ,则图中摆盘的面积是( )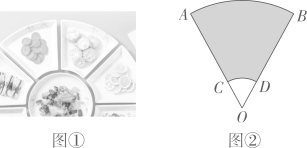 A、 B、 C、 D、9. 竖直上抛物体离地面的高度 与运动时间 之间的关系可以近似地用公式 表示,其中 是物体抛出时离地面的高度, 是物体抛出时的速度.某人将一个小球从距地面 的高处以 的速度竖直向上抛出,小球达到的离地面的最大高度为( )A、 B、 C、 D、10. 如图是一张矩形纸板,顺次连接各边中点得到菱形,再顺次连接菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是( )
A、 B、 C、 D、9. 竖直上抛物体离地面的高度 与运动时间 之间的关系可以近似地用公式 表示,其中 是物体抛出时离地面的高度, 是物体抛出时的速度.某人将一个小球从距地面 的高处以 的速度竖直向上抛出,小球达到的离地面的最大高度为( )A、 B、 C、 D、10. 如图是一张矩形纸板,顺次连接各边中点得到菱形,再顺次连接菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是( )
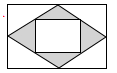 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: .12. 如图是一组有规律的图案,它们是由边长相等的正三角形组合而成,第 个图案有 个三角形,第 个图案有 个三角形,第 个图案有 个三角形 按此规律摆下去,第 个图案有个三角形(用含 的代数式表示).
 13. 某校为了选拔一名百米赛跑运动员参加市中学生运动会,组织了 次预选赛,其中甲,乙两名运动员较为突出,他们在 次预选赛中的成绩(单位:秒)如下表所示:
13. 某校为了选拔一名百米赛跑运动员参加市中学生运动会,组织了 次预选赛,其中甲,乙两名运动员较为突出,他们在 次预选赛中的成绩(单位:秒)如下表所示:甲
乙
由于甲,乙两名运动员的成绩的平均数相同,学校决定依据他们成绩的稳定性进行选拔,那么被选中的运动员是 .
14. 如图是一张长 ,宽 的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积 是的有盖的长方体铁盒.则剪去的正方形的边长为 .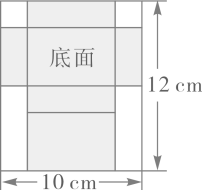 15. 如图,在 中, , , , ,垂足为 , 为 的中点, 与 交于点 ,则 的长为 .
15. 如图,在 中, , , , ,垂足为 , 为 的中点, 与 交于点 ,则 的长为 .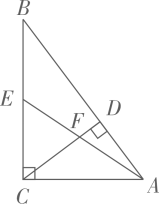
三、解答题
-
16.(1)、计算:(2)、下面是小彬同学进行分式化简的过程,请认真阅读并完成相应任务.
第一步
第二步
第三步
第四步
第五步
第六步
任务一:填空:①以上化简步骤中,第步是进行分式的通分,通分的依据是或填为;
②第步开始出现不符合题意,这一步错误的原因是;
(3)、任务二:请直接写出该分式化简后的正确结果;解;
.
任务三:除纠正上述错误外,请你根据平时的学习经验,就分式化简时还需要注意的事项给其他同学提一条建议.
17. 年 月份,省城太原开展了“活力太原·乐购晋阳”消费暖心活动,本次活动中的家电消费券单笔交易满 元立减 元(每次只能使用一张)某品牌电饭煲按进价提高 后标价,若按标价的八折销售,某顾客购买该电饭煲时,使用一张家电消费券后,又付现金 元.求该电饭煲的进价. 18. 如图,四边形 是平行四边形,以点 为圆心, 为半径的 与 相切于点 ,与 相交于点 , 的延长线交 于点 ,连接 交 于点 ,求 和 的度数.
18. 如图,四边形 是平行四边形,以点 为圆心, 为半径的 与 相切于点 ,与 相交于点 , 的延长线交 于点 ,连接 交 于点 ,求 和 的度数.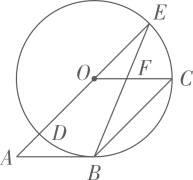 19. 年国家提出并部署了“新基建”项目,主要包含“特高压,城际高速铁路和城市轨道交通, 基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩”等.《 新基建中高端人才市场就业吸引力报告》重点刻画了“新基建”中五大细分领域( 基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩)总体的人才与就业机会.下图是其中的一个统计图.
19. 年国家提出并部署了“新基建”项目,主要包含“特高压,城际高速铁路和城市轨道交通, 基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩”等.《 新基建中高端人才市场就业吸引力报告》重点刻画了“新基建”中五大细分领域( 基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩)总体的人才与就业机会.下图是其中的一个统计图.请根据图中信息,解答下列问题:
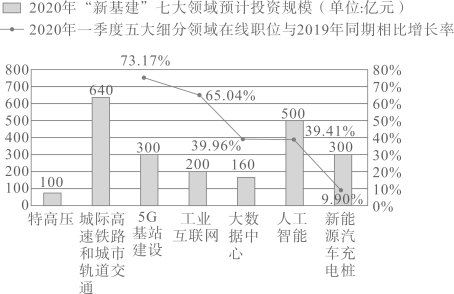 (1)、填空:图中 年“新基建”七大领域预计投资规模的中位数是亿元;(2)、甲,乙两位待业人员,仅根据上面统计图中的数据,从五大细分领域中分别选择了“ 基站建设”和“人工智能”作为自己的就业方向,请简要说明他们选择就业方向的理由各是什么;(3)、小勇对“新基建”很感兴趣,他收集到了五大细分领域的图标,依次制成编号为 , , , , 的五张卡片(除编号和内容外,其余完全相同),将这五张卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张.请用列表或画树状图的方法求抽到的两张卡片恰好是编号为 ( 基站建设)和 (人工智能)的概率.
(1)、填空:图中 年“新基建”七大领域预计投资规模的中位数是亿元;(2)、甲,乙两位待业人员,仅根据上面统计图中的数据,从五大细分领域中分别选择了“ 基站建设”和“人工智能”作为自己的就业方向,请简要说明他们选择就业方向的理由各是什么;(3)、小勇对“新基建”很感兴趣,他收集到了五大细分领域的图标,依次制成编号为 , , , , 的五张卡片(除编号和内容外,其余完全相同),将这五张卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张.请用列表或画树状图的方法求抽到的两张卡片恰好是编号为 ( 基站建设)和 (人工智能)的概率. 20. 阅读与思考
20. 阅读与思考下面是小宇同学的数学日记,请仔细阅读并完成相应的任务.
×年×月×日 星期日
没有直角尺也能作出直角
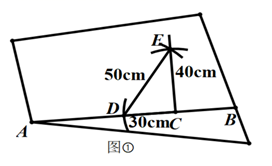
今天,我在书店一本书上看到下面材料:木工师傅有一块如图①所示的四边形木板,他已经在木板上画出一条裁割线 ,现根据木板的情况,要过 上的一点 ,作出 的垂线,用锯子进行裁割,然而手头没有直角尺,怎么办呢?
办法一:如图①,可利用一把有刻度的直尺在 上量出 ,然后分别以 , 为圆心,以 与 为半径画圆弧,两弧相交于点 ,作直线 ,则 必为 .

办法二:如图②,可以取一根笔直的木棒,用铅笔在木棒上点出 , 两点,然后把木棒斜放在木板上,使点 与点 重合,用铅笔在木板上将点 对应的位置标记为点 ,保持点 不动,将木棒绕点 旋转,使点 落在 上,在木板上将点 对应的位置标记为点 .然后将 延长,在延长线上截取线段 ,得到点 ,作直线 ,则 .
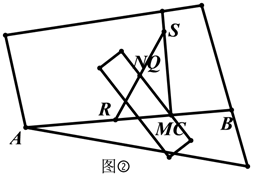
我有如下思考:以上两种办法依据的是什么数学原理呢?我还有什么办法不用直角尺也能作出垂线呢?
……
任务:
(1)、填空;“办法一”依据的一个数学定理是;(2)、根据“办法二”的操作过程,证明 ;(3)、①尺规作图:请在图③的木板上,过点 作出 的垂线(在木板上保留作图痕迹,不写作法);②说明你的作法依据的数学定理或基本事实(写出一个即可)
21. 图①是某车站的一组智能通道闸机,当行人通过时智能闸机会自动识别行人身份,识别成功后,两侧的圆弧翼闸会收回到两侧闸机箱内,这时行人即可通过.图②是两圆弧翼展开时的截面图,扇形 和 是闸机的“圆弧翼”,两圆弧翼成轴对称, 和 均垂直于地面,扇形的圆心角 ,半径 ,点 与点 在同一水平线上,且它们之间的距离为 . (1)、求闸机通道的宽度,即 与 之间的距离(参考数据: , , );(2)、经实践调查,一个智能闸机的平均检票速度是一个人工检票口平均检票速度的 倍, 人的团队通过一个智能闸机口比通过一个人工检票口可节约 分钟,求一个智能闸机平均每分钟检票通过的人数.22. 综合与实践
(1)、求闸机通道的宽度,即 与 之间的距离(参考数据: , , );(2)、经实践调查,一个智能闸机的平均检票速度是一个人工检票口平均检票速度的 倍, 人的团队通过一个智能闸机口比通过一个人工检票口可节约 分钟,求一个智能闸机平均每分钟检票通过的人数.22. 综合与实践问题情境:
如图①,点 为正方形 内一点, ,将 绕点 按顺时针方向旋转 ,得到 (点 的对应点为点 ),延长 交 于点 ,连接 .
猜想证明:
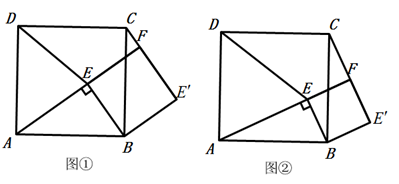 (1)、试判断四边形 的形状,并说明理由;(2)、如图②,若 ,请猜想线段 与 的数量关系并加以证明;
(1)、试判断四边形 的形状,并说明理由;(2)、如图②,若 ,请猜想线段 与 的数量关系并加以证明;解决问题:
(3)、如图①,若 , ,请直接写出 的长.23. 综合与探究如图,抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 .直线 与抛物线交于 , 两点,与 轴交于点 ,点 的坐标为 .
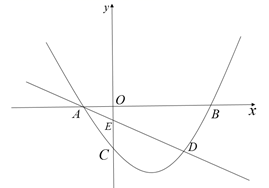 (1)、请直接写出 , 两点的坐标及直线 的函数表达式;(2)、若点 是抛物线上的点,点 的横坐标为 ,过点 作 轴,垂足为 . 与直线 交于点 ,当点 是线段 的三等分点时,求点 的坐标;(3)、若点 是 轴上的点,且 ,求点 的坐标.
(1)、请直接写出 , 两点的坐标及直线 的函数表达式;(2)、若点 是抛物线上的点,点 的横坐标为 ,过点 作 轴,垂足为 . 与直线 交于点 ,当点 是线段 的三等分点时,求点 的坐标;(3)、若点 是 轴上的点,且 ,求点 的坐标.