内蒙古通辽市2020年中考数学试卷
试卷更新日期:2020-08-12 类型:中考真卷
一、单选题
-
1. 2020年我市初三毕业生超过30000人,将30000用科学记数法表示正确的是( )A、 B、 C、 D、3万2. 下列说法错误的是( )A、 是2个数a的和 B、 是2和数a的积 C、 是单项式 D、 是偶数3. 下列事件中是不可能事件的是( )A、守株待兔 B、瓮中捉鳖 C、水中捞月 D、百步穿杨4. 如图,将一副三角尺按下列位置摆放,使 和 互余的摆放方式是( )A、
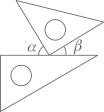 B、
B、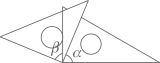 C、
C、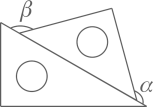 D、
D、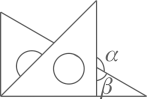 5. 若关于x的方程kx2﹣6x+9=0有实数根,则k的取值范围是( )A、k<1 B、k≤1 C、k<1且k≠0 D、k≤1且k≠06. 根据圆规作图的痕迹,可用直尺成功地找到三角形内心的是( )A、
5. 若关于x的方程kx2﹣6x+9=0有实数根,则k的取值范围是( )A、k<1 B、k≤1 C、k<1且k≠0 D、k≤1且k≠06. 根据圆规作图的痕迹,可用直尺成功地找到三角形内心的是( )A、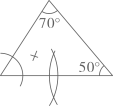 B、
B、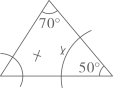 C、
C、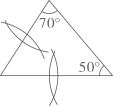 D、
D、 7. 如图, 分别与 相切于 两点, ,则 ( )
7. 如图, 分别与 相切于 两点, ,则 ( )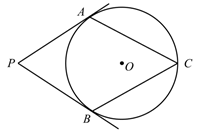 A、 B、 C、 D、8. 如图, 是 的中线,四边形 是平行四边形,增加下列条件,能判断 是菱形的是( )
A、 B、 C、 D、8. 如图, 是 的中线,四边形 是平行四边形,增加下列条件,能判断 是菱形的是( ) A、 B、 C、 D、9. 如图, 交双曲线 于点A , 且 ,若矩形 的面积是8,且 轴,则k的值是( )
A、 B、 C、 D、9. 如图, 交双曲线 于点A , 且 ,若矩形 的面积是8,且 轴,则k的值是( )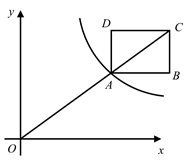 A、18 B、50 C、12 D、10. 从下列命题中,随机抽取一个是真命题的概率是( )
A、18 B、50 C、12 D、10. 从下列命题中,随机抽取一个是真命题的概率是( )⑴无理数都是无限小数;
⑵因式分解 ;
⑶棱长是 的正方体的表面展开图的周长一定是 ;
⑷弧长是 ,面积是 的扇形的圆心角是 .
A、 B、 C、 D、1二、填空题
-
11. 计算:
; ; .
12. 若数据3,a , 3,5,3的平均数是3,则这组数据众数是;a的值是;方差是 .13. 如图,点O在直线 上, ,则 的度数是 . 14. 如图,用大小相同的小正方形拼大正方形,拼第1个正方形需要4个小正方形,拼第2个正方形需要9个小正方形……,按这样的方法拼成的第 个正方形比第n个正方形多个小正方形.
14. 如图,用大小相同的小正方形拼大正方形,拼第1个正方形需要4个小正方形,拼第2个正方形需要9个小正方形……,按这样的方法拼成的第 个正方形比第n个正方形多个小正方形.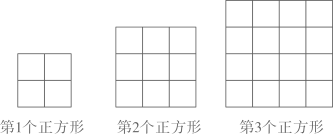 15. 有一个人患了新冠肺炎,经过两轮传染后共有169人患了新冠肺炎,每轮传染中平均一个人传染了个人.16. 如图,在 中, ,点P在斜边 上,以 为直角边作等腰直角三角形 , ,则 三者之间的数量关系是 .
15. 有一个人患了新冠肺炎,经过两轮传染后共有169人患了新冠肺炎,每轮传染中平均一个人传染了个人.16. 如图,在 中, ,点P在斜边 上,以 为直角边作等腰直角三角形 , ,则 三者之间的数量关系是 . 17. 如图①,在 中, ,点E是边 的中点,点P是边 上一动点,设 .图②是y关于x的函数图象,其中H是图象上的最低点..那么 的值为 .
17. 如图①,在 中, ,点E是边 的中点,点P是边 上一动点,设 .图②是y关于x的函数图象,其中H是图象上的最低点..那么 的值为 .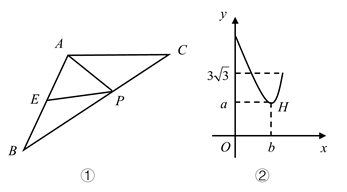
三、解答题
-
18. 解方程: .19. 从A处看一栋楼顶部的仰角为 ,看这栋楼底部的俯角为 ,A处与楼的水平距离 为 ,若 ,求这栋楼高.
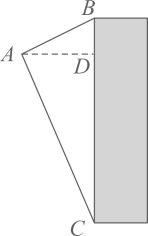 20. 用※定义一种新运算:对于任意实数m和n , 规定 ,如: .
20. 用※定义一种新运算:对于任意实数m和n , 规定 ,如: . (1)、求 ;(2)、若 ,求m的取值范围,并在所给的数轴上表示出解集.21. 甲口袋中装有2个相同小球,它们分别写有数字1,2;乙口袋中装有3个相同小球,它们分别写有数字3,4,5;丙口袋中装有2个相同小球,它们分别写有数字6,7.从三个口袋各随机取出1个小球.用画树状图或列表法求:(1)、取出的3个小球上恰好有一个偶数的概率;(2)、取出的3个小球上全是奇数的概率.22. 如图, 的直径 交弦(不是直径) 于点P , 且 .求证: .
(1)、求 ;(2)、若 ,求m的取值范围,并在所给的数轴上表示出解集.21. 甲口袋中装有2个相同小球,它们分别写有数字1,2;乙口袋中装有3个相同小球,它们分别写有数字3,4,5;丙口袋中装有2个相同小球,它们分别写有数字6,7.从三个口袋各随机取出1个小球.用画树状图或列表法求:(1)、取出的3个小球上恰好有一个偶数的概率;(2)、取出的3个小球上全是奇数的概率.22. 如图, 的直径 交弦(不是直径) 于点P , 且 .求证: .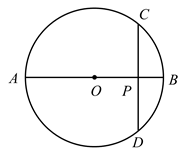 23. 某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
23. 某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题: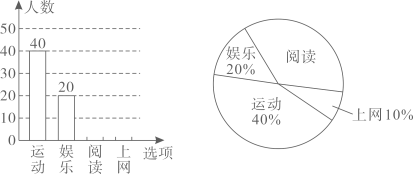 (1)、在这次调查中,共调查了多少名学生;(2)、补全条形统计图;(3)、若该校爱好运动的学生共有800名,则该校学生总数大约有多少名.24. 某服装专卖店计划购进 两种型号的精品服装.已知2件A型服装和3件B型服装共需4600元;1件A型服装和2件B型服装共需2800元.(1)、求 型服装的单价;(2)、专卖店要购进 两种型号服装60件,其中A型件数不少于B型件数的2倍,如果B型打七五折,那么该专卖店至少需要准备多少货款?25. 中心为O的正六边形 的半径为 .点 同时分别从 两点出发,以 的速度沿 向终点 运动,连接 ,设运动时间为 .
(1)、在这次调查中,共调查了多少名学生;(2)、补全条形统计图;(3)、若该校爱好运动的学生共有800名,则该校学生总数大约有多少名.24. 某服装专卖店计划购进 两种型号的精品服装.已知2件A型服装和3件B型服装共需4600元;1件A型服装和2件B型服装共需2800元.(1)、求 型服装的单价;(2)、专卖店要购进 两种型号服装60件,其中A型件数不少于B型件数的2倍,如果B型打七五折,那么该专卖店至少需要准备多少货款?25. 中心为O的正六边形 的半径为 .点 同时分别从 两点出发,以 的速度沿 向终点 运动,连接 ,设运动时间为 .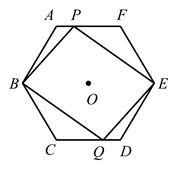 (1)、求证:四边形 为平行四边形;(2)、求矩形 的面积与正六边形 的面积之比.26. 如图,在平面直角坐标系中,抛物线 与x轴交于点 ,与y轴交于点C , 且直线 过点B , 与y轴交于点D , 点C与点D关于x轴对称.点P是线段 上一动点,过点P作x轴的垂线交抛物线于点M , 交直线 于点N .
(1)、求证:四边形 为平行四边形;(2)、求矩形 的面积与正六边形 的面积之比.26. 如图,在平面直角坐标系中,抛物线 与x轴交于点 ,与y轴交于点C , 且直线 过点B , 与y轴交于点D , 点C与点D关于x轴对称.点P是线段 上一动点,过点P作x轴的垂线交抛物线于点M , 交直线 于点N . (1)、求抛物线的函数解析式;(2)、当 的面积最大时,求点P的坐标;(3)、在(2)的条件下,在y轴上是否存在点Q , 使得以 三点为顶点的三角形是直角三角形,若存在,直接写出点Q的坐标;若不存在,说明理由.
(1)、求抛物线的函数解析式;(2)、当 的面积最大时,求点P的坐标;(3)、在(2)的条件下,在y轴上是否存在点Q , 使得以 三点为顶点的三角形是直角三角形,若存在,直接写出点Q的坐标;若不存在,说明理由.