内蒙古呼和浩特市2020年中考数学试卷
试卷更新日期:2020-08-12 类型:中考真卷
一、单选题
-
1. 下面四幅图是我国传统文化与艺术中的几个经典图案,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 2020年3月抗击“新冠肺炎”居家学习期间,小华计划每天背诵6个汉语成语.将超过的个数记为正数,不足的个数记为负数,某一周连续5天的背诵记录如下: ,0, , , ,则这5天他共背诵汉语成语( )A、38个 B、36个 C、34个 D、30个3. 下列运算正确的是( )A、 B、 C、 D、4. 已知电流在一定时间段内正常通过电子元件“
2. 2020年3月抗击“新冠肺炎”居家学习期间,小华计划每天背诵6个汉语成语.将超过的个数记为正数,不足的个数记为负数,某一周连续5天的背诵记录如下: ,0, , , ,则这5天他共背诵汉语成语( )A、38个 B、36个 C、34个 D、30个3. 下列运算正确的是( )A、 B、 C、 D、4. 已知电流在一定时间段内正常通过电子元件“ ”的概率是0.5;则在一定时间段内,由该元件组成的图示电路A、B之间,电流能够正常通过的概率是( )
”的概率是0.5;则在一定时间段内,由该元件组成的图示电路A、B之间,电流能够正常通过的概率是( )  A、0.75 B、0.625 C、0.5 D、0.255. 中国古代数学著作《算法统宗》中有这样一段记载,“三百七十八里关;初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是;有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到关口,则此人第一和第六这两天共走了( )A、102里 B、126里 C、192里 D、198里6. 已知二次函数 ,当x取互为相反数的任意两个实数值时,对应的函数值y总相等,则关于x的一元二次方程 的两根之积为( )A、0 B、 C、 D、7. 关于二次函数 ,下列说法错误的是( )A、若将图象向上平移10个单位,再向左平移2个单位后过点 ,则 B、当 时,y有最小值 C、 对应的函数值比最小值大7 D、当 时,图象与x轴有两个不同的交点8. 命题①设 的三个内角为A、B、C且 ,则 、 、 中,最多有一个锐角;②顺次连接菱形各边中点所得的四边形是矩形;③从11个评委分别给出某选手的不同原始评分中,去掉1个最高分、1个最低分,剩下的9个评分与11个原始评分相比,中位数和方差都不发生变化.其中错误命题的个数为( )A、0个 B、1个 C、2个 D、3个9. 在同一坐标系中,若正比例函数 与反比例函数 的图象没有交点,则 与 的关系,下面四种表述① ;② 或 ;③ ;④ .正确的有( )A、4个 B、3个 C、2个 D、1个10. 如图,把某矩形纸片 沿 , 折叠(点E、H在 边上,点F,G在 边上),使点B和点C落在 边上同一点P处,A点的对称点为 、D点的对称点为 ,若 , 为8, 的面积为2,则矩形 的长为( )
A、0.75 B、0.625 C、0.5 D、0.255. 中国古代数学著作《算法统宗》中有这样一段记载,“三百七十八里关;初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是;有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到关口,则此人第一和第六这两天共走了( )A、102里 B、126里 C、192里 D、198里6. 已知二次函数 ,当x取互为相反数的任意两个实数值时,对应的函数值y总相等,则关于x的一元二次方程 的两根之积为( )A、0 B、 C、 D、7. 关于二次函数 ,下列说法错误的是( )A、若将图象向上平移10个单位,再向左平移2个单位后过点 ,则 B、当 时,y有最小值 C、 对应的函数值比最小值大7 D、当 时,图象与x轴有两个不同的交点8. 命题①设 的三个内角为A、B、C且 ,则 、 、 中,最多有一个锐角;②顺次连接菱形各边中点所得的四边形是矩形;③从11个评委分别给出某选手的不同原始评分中,去掉1个最高分、1个最低分,剩下的9个评分与11个原始评分相比,中位数和方差都不发生变化.其中错误命题的个数为( )A、0个 B、1个 C、2个 D、3个9. 在同一坐标系中,若正比例函数 与反比例函数 的图象没有交点,则 与 的关系,下面四种表述① ;② 或 ;③ ;④ .正确的有( )A、4个 B、3个 C、2个 D、1个10. 如图,把某矩形纸片 沿 , 折叠(点E、H在 边上,点F,G在 边上),使点B和点C落在 边上同一点P处,A点的对称点为 、D点的对称点为 ,若 , 为8, 的面积为2,则矩形 的长为( )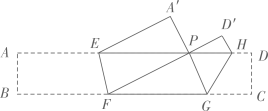 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图, 中, 为 的中点,以 为圆心, 长为半径画一弧交 于 点,若 , , ,则扇形 的面积为 .
 12. 一个几何体的三视图如图所示,则该几何体的表面积为 .
12. 一个几何体的三视图如图所示,则该几何体的表面积为 . 13. 分式 与 的最简公分母是 , 方程 的解是 .14. 公司以3元/ 的成本价购进 柑橘,并希望出售这些柑橘能够获得12000元利润,在出售柑橘(去掉损坏的柑橘)时,需要先进行“柑橘损坏率”统计,再大约确定每千克柑橘的售价,右面是销售部通过随机取样,得到的“柑橘损坏率”统计表的一部分,由此可估计柑橘完好的概率为(精确到0.1);从而可大约每千克柑橘的实际售价为元时(精确到0.1),可获得12000元利润.
13. 分式 与 的最简公分母是 , 方程 的解是 .14. 公司以3元/ 的成本价购进 柑橘,并希望出售这些柑橘能够获得12000元利润,在出售柑橘(去掉损坏的柑橘)时,需要先进行“柑橘损坏率”统计,再大约确定每千克柑橘的售价,右面是销售部通过随机取样,得到的“柑橘损坏率”统计表的一部分,由此可估计柑橘完好的概率为(精确到0.1);从而可大约每千克柑橘的实际售价为元时(精确到0.1),可获得12000元利润.柑橘总质量
损坏柑橘质量
柑橘损坏的频率 (精确到0.001)
…
…
…
250
24.75
0.099
300
30.93
0.103
350
35.12
0.100
450
44.54
0.099
500
50.62
0.101
15. “书法艺求课”开课后,某同学买了一包纸练习软笔书法,且每逢星期几写几张,即每星期一写1张,每星期二写2张,……,每星期日写7张,若该同学从某年的5月1日开始练习,到5月30日练习完后累积写完的宣纸总数过120张,则可算得5月1日到5月28日他共用宣纸张数为 , 并可推断出5月30日应该是星期几 .16. 已知 为⊙O的直径且长为 , 为⊙O上异于A,B的点,若 与过点C的⊙O的切线互相垂直,垂足为D.①若等腰三角形 的顶角为120度,则 ;②若 为正三角形,则 ;③若等腰三角形 的对称轴经过点D,则 ;④无论点C在何处,将 沿 折叠,点D一定落在直径 上,其中正确结论的序号为 .三、解答题
-
17.(1)、计算: ;(2)、已知m是小于0的常数,解关于x的不等式组: .18. 如图,正方形 ,G是 边上任意一点(不与B、C重合), 于点E, ,且交 于点F.
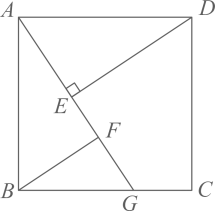 (1)、求证: ;(2)、四边形 是否可能是平行四边形,如果可能请指出此时点G的位置,如不可能请说明理由.19. 如图,一艘船由A港沿北偏东65°方向航行 到B港,然后再沿北偏西42°方向航行至C港,已知C港在A港北偏东20°方向.
(1)、求证: ;(2)、四边形 是否可能是平行四边形,如果可能请指出此时点G的位置,如不可能请说明理由.19. 如图,一艘船由A港沿北偏东65°方向航行 到B港,然后再沿北偏西42°方向航行至C港,已知C港在A港北偏东20°方向. (1)、直接写出 的度数;(2)、求A、C两港之间的距离.(结果用含非特殊角的三角函数及根式表示即可)20. 已知自变量x与因变量 的对应关系如下表呈现的规律.
(1)、直接写出 的度数;(2)、求A、C两港之间的距离.(结果用含非特殊角的三角函数及根式表示即可)20. 已知自变量x与因变量 的对应关系如下表呈现的规律.x
…
0
1
2
…
…
12
11
10
9
8
…
(1)、直接写出函数解析式及其图象与x轴和y轴的交点M,N的坐标;(2)、设反比例函数 的图象与(1)求得的函数的图象交于A,B两点,O为坐标原点且 ,求反比例函数解析式;已知 ,点 与 分别在反比例函数与(1)求得的函数的图象上,直接写出 与 的大小关系.21. 为了发展学生的健康情感,学校开展多项体育活动比赛,促进学生加强体育锻炼,注重增强体质,从全校2100名学生60秒跳绳比赛成绩中,随机抽取60名同学的成绩,通过分组整理数据得到下面的样本频数分布表.跳绳的次数
频数
4
6
11
22
10
4
(1)、已知样本中最小的数是60,最大的数是198,组距是20,请你将该表左侧的每组数据补充完整;(2)、估计全校学生60秒跳绳成绩能达到最好一组成绩的人数;(3)、若以各组组中值代表各组的实际数据,求出样本平均数(结果保留整数)及众数;分别写出用样本平均数和众数估计全校学生60秒跳绳成绩得到的推断性结论.22. “通过等价变换,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方式,例如:解方程 ,就可以利用该思维方式,设 ,将原方程转化为: 这个熟悉的关于y的一元二次方程,解出y,再求x,这种方法又叫“换元法”.请你用这种思维方式和换元法解决下面的问题.已知实数x,y满足 ,求 的值.23. 某同学在学习了正多边形和圆之后,对正五边形的边及相关线段进行研究,发现多处出现者名的黄金分割比 .如图,圆内接正五边形 ,圆心为O, 与 交于点H, 、 与 分别交于点M、N.根据圆与正五边形的对称性,只对部分图形进行研究.(其它可同理得出) (1)、求证: 是等腰三角形且底角等于36°,并直接说出 的形状;(2)、求证: ,且其比值 ;(3)、由对称性知 ,由(1)(2)可知 也是一个黄金分割数,据此求 的值.24. 已知某厂以 小时/千克的速度匀速生产某种产品(生产条件要求 ),且每小时可获得利润 元.(1)、某人将每小时获得的利润设为y元,发现 时, ,所以得出结论:每小时获得的利润,最少是180元,他是依据什么得出该结论的,用你所学数学知识帮他进行分析说明;(2)、若以生产该产品2小时获得利润1800元的速度进行生产,则1天(按8小时计算)可生产该产品多少千克;(3)、要使生产680千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.
(1)、求证: 是等腰三角形且底角等于36°,并直接说出 的形状;(2)、求证: ,且其比值 ;(3)、由对称性知 ,由(1)(2)可知 也是一个黄金分割数,据此求 的值.24. 已知某厂以 小时/千克的速度匀速生产某种产品(生产条件要求 ),且每小时可获得利润 元.(1)、某人将每小时获得的利润设为y元,发现 时, ,所以得出结论:每小时获得的利润,最少是180元,他是依据什么得出该结论的,用你所学数学知识帮他进行分析说明;(2)、若以生产该产品2小时获得利润1800元的速度进行生产,则1天(按8小时计算)可生产该产品多少千克;(3)、要使生产680千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.