内蒙古包头市2020年中考数学试卷
试卷更新日期:2020-08-12 类型:中考真卷
一、单选题
-
1. 的计算结果是( )A、5 B、 C、 D、2. 2020年初,国家统计局发布数据,按现行国家农村贫困标准测算,截至2019年末,全国农村贫困人口减少至551万人,累计减少9348万人.将9348万用科学记数法表示为( )A、 B、 C、 D、3. 点A在数轴上,点A所对应的数用 表示,且点A到原点的距离等于3,则a的值为( )A、 或1 B、 或2 C、 D、14. 下列计算结果正确的是( )A、 B、 C、 D、5. 如图, 是 的外角, .若 , ,则 的度数为( )
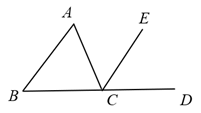 A、 B、 C、 D、6. 如图,将小立方块①从6个大小相同的小立方块所搭的几何体中移走后,所得几何体( )
A、 B、 C、 D、6. 如图,将小立方块①从6个大小相同的小立方块所搭的几何体中移走后,所得几何体( )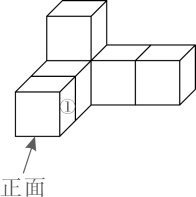 A、主视图改变,左视图改变 B、俯视图不变,左视图改变 C、俯视图改变,左视图改变 D、主视图不变,左视图不变7. 两组数据:3,a , b , 5与a , 4, 的平均数都是3.若将这两组数据合并为一组新数据,则这组新数据的众数为( )A、2 B、3 C、4 D、58. 如图,在 中, ,D是 的中点, ,交 的延长线于点E . 若 , ,则 的长为( )
A、主视图改变,左视图改变 B、俯视图不变,左视图改变 C、俯视图改变,左视图改变 D、主视图不变,左视图不变7. 两组数据:3,a , b , 5与a , 4, 的平均数都是3.若将这两组数据合并为一组新数据,则这组新数据的众数为( )A、2 B、3 C、4 D、58. 如图,在 中, ,D是 的中点, ,交 的延长线于点E . 若 , ,则 的长为( ) A、 B、 C、 D、9. 如图, 是 的直径, 是弦,点 在直径 的两侧.若 , ,则 的长为( )
A、 B、 C、 D、9. 如图, 是 的直径, 是弦,点 在直径 的两侧.若 , ,则 的长为( ) A、 B、 C、 D、10. 下列命题正确的是( )A、若分式 的值为0,则x的值为±2. B、一个正数的算术平方根一定比这个数小. C、若 ,则 . D、若 ,则一元二次方程 有实数根.11. 如图,在平面直角坐标系中,直线 与x轴、y轴分别交于点A和点 是线段 上一点,过点C作 轴,垂足为D , 轴,垂足为E , .若双曲线 经过点C , 则k的值为( )
A、 B、 C、 D、10. 下列命题正确的是( )A、若分式 的值为0,则x的值为±2. B、一个正数的算术平方根一定比这个数小. C、若 ,则 . D、若 ,则一元二次方程 有实数根.11. 如图,在平面直角坐标系中,直线 与x轴、y轴分别交于点A和点 是线段 上一点,过点C作 轴,垂足为D , 轴,垂足为E , .若双曲线 经过点C , 则k的值为( )
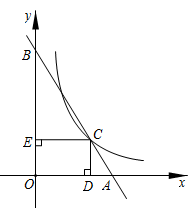 A、 B、 C、 D、12. 如图,在 中, , ,按以下步骤作图:(1)分别以点 为圆心,以大于 的长为半径作弧,两弧相交于 两点(点M在 的上方);(2)作直线 交 于点O , 交 于点D;(3)用圆规在射线 上截取 .连接 ,过点O作 ,垂足为F , 交 于点G . 下列结论:
A、 B、 C、 D、12. 如图,在 中, , ,按以下步骤作图:(1)分别以点 为圆心,以大于 的长为半径作弧,两弧相交于 两点(点M在 的上方);(2)作直线 交 于点O , 交 于点D;(3)用圆规在射线 上截取 .连接 ,过点O作 ,垂足为F , 交 于点G . 下列结论:① ;② ;③ ;④若 ,则四边形 的周长为25.
其中正确的结论有( )
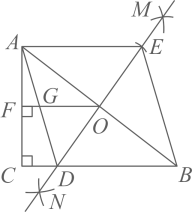 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 在函数 中,自变量 的取值范围是 .14. 分式方程 的解是 .15. 计算: .16. 如图,在正方形 ABCD ,E是对角线 BD 上一点, AE 的延长线交 CD 于点F , 连接 CE .若∠BAE=56° ,则 ∠CEF= ° .
 17. 一个不透明的盒子里放置三张完全相同的卡片,分别标有数字1,2,3.随机抽取1张,放回后再随机抽取1张,则抽得的第二张卡片上的数字大于第一张卡片上的数字的概率为 .18. 如图,在平行四边形 中, 的平分线与 的平分线交于点E , 若点E恰好在边 上,则 的值为 .
17. 一个不透明的盒子里放置三张完全相同的卡片,分别标有数字1,2,3.随机抽取1张,放回后再随机抽取1张,则抽得的第二张卡片上的数字大于第一张卡片上的数字的概率为 .18. 如图,在平行四边形 中, 的平分线与 的平分线交于点E , 若点E恰好在边 上,则 的值为 .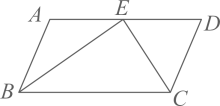 19. 在平面直角坐标系中,已知 和 是抛物线 上的两点,将抛物线 的图象向上平移n(n是正整数)个单位,使平移后的图象与x轴没有交点,则n的最小值为 .20. 如图,在矩形 中, 是对角线, ,垂足为E , 连接 .若 ,则如 的值为 .
19. 在平面直角坐标系中,已知 和 是抛物线 上的两点,将抛物线 的图象向上平移n(n是正整数)个单位,使平移后的图象与x轴没有交点,则n的最小值为 .20. 如图,在矩形 中, 是对角线, ,垂足为E , 连接 .若 ,则如 的值为 .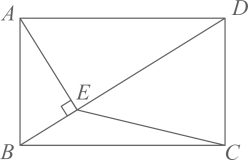
三、解答题
-
21. 我国 技术发展迅速,全球领先.某公司最新推出一款 产品,为了解用户对该产品的满意度,随机调查了30个用户,得到用户对该产品的满意度评分如下(单位:分):
83 92 68 55 77 71 73 62 73 95 92 94 72 64 59
66 71 75 69 86 87 79 81 77 68 82 62 77 61 88
整理上面的数据得到尚不完整的频数直方图(如图).请根据所给信息,解答下列问题:
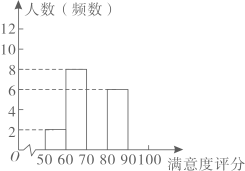 (1)、补全频数直方图;(2)、参与调查的一个用户说:“我的满意度评分在这30个用户中是中位数”,该用户的满意度评分是分;(3)、根据用户满意度评分,将用户的满意度从低到高分为三个等级:
(1)、补全频数直方图;(2)、参与调查的一个用户说:“我的满意度评分在这30个用户中是中位数”,该用户的满意度评分是分;(3)、根据用户满意度评分,将用户的满意度从低到高分为三个等级:满意度评分
低于60分
60分到89分
不低于90分
满意度等级
不满意
满意
非常满意
估计使用该公司这款 产品的1500个用户中,满意度等级为“非常满意”的人数.
22. 如图,一个人骑自行车由A地到C地途经B地当他由A地出发时,发现他的北偏东 方向有一电视塔P , 他由A地向正北方向骑行了 到达B地,发现电视塔P在他北偏东 方向,然后他由B地向北偏东 方向骑行了 到达C地.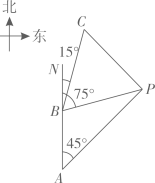 (1)、求A地与电视塔P的距离;(2)、求C地与电视塔P的距离.23. 某商店销售 两种商品,A种商品的销售单价比B种商品的销售单价少40元,2件A种商品和3件B种商品的销售总额为820元.(1)、求A种商品和B种商品的销售单价分别为多少元?(2)、该商店计划购进 两种商品共60件,且 两种商品的进价总额不超过7800元,已知A种商品和B种商品的每件进价分别为110元和140元,应如何进货才能使这两种商品全部售出后总获利最多?24. 如图, 是 的直径,半径 ,垂足为O , 直线l为 的切线,A是切点,D是 上一点, 的延长线交直线l于点 是 上一点, 的延长线交 于点G , 连接 ,已知 的半径为3, , .
(1)、求A地与电视塔P的距离;(2)、求C地与电视塔P的距离.23. 某商店销售 两种商品,A种商品的销售单价比B种商品的销售单价少40元,2件A种商品和3件B种商品的销售总额为820元.(1)、求A种商品和B种商品的销售单价分别为多少元?(2)、该商店计划购进 两种商品共60件,且 两种商品的进价总额不超过7800元,已知A种商品和B种商品的每件进价分别为110元和140元,应如何进货才能使这两种商品全部售出后总获利最多?24. 如图, 是 的直径,半径 ,垂足为O , 直线l为 的切线,A是切点,D是 上一点, 的延长线交直线l于点 是 上一点, 的延长线交 于点G , 连接 ,已知 的半径为3, , .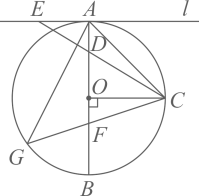 (1)、求 的长;(2)、求 的值及 的长.25. 如图,在 中, , , 绕点C按顺时针方向旋转得到 , 与 交于点D .(1)、如图,当 时,过点B作 ,垂足为E , 连接 .
(1)、求 的长;(2)、求 的值及 的长.25. 如图,在 中, , , 绕点C按顺时针方向旋转得到 , 与 交于点D .(1)、如图,当 时,过点B作 ,垂足为E , 连接 .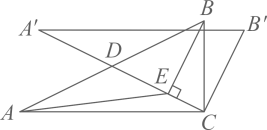
①求证: ;
②求 的值;
(2)、如图,当 时,过点D作 ,交 于点N , 交 的延长线于点M , 求 的值.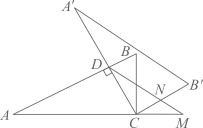 26. 如图,在平面直角坐标系中,抛物线 经过坐标原点,与x轴正半轴交于点A , 该抛物线的顶点为M , 直线 经过点A , 与y轴交于点B , 连接 .
26. 如图,在平面直角坐标系中,抛物线 经过坐标原点,与x轴正半轴交于点A , 该抛物线的顶点为M , 直线 经过点A , 与y轴交于点B , 连接 .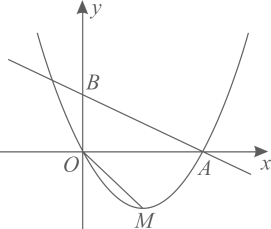
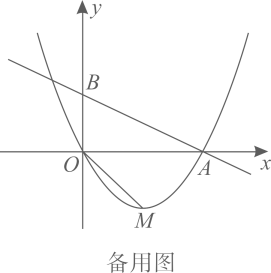 (1)、求b的值及点M的坐标;(2)、将直线 向下平移,得到过点M的直线 ,且与x轴负半轴交于点C , 取点 ,连接 ,求证: :(3)、点E是线段 上一动点,点F是线段 上一动点,连接 ,线段 的延长线与线段 交于点G . 当 时,是否存在点E , 使得 ?若存在,求出点E的坐标;若不存在,请说明理由.
(1)、求b的值及点M的坐标;(2)、将直线 向下平移,得到过点M的直线 ,且与x轴负半轴交于点C , 取点 ,连接 ,求证: :(3)、点E是线段 上一动点,点F是线段 上一动点,连接 ,线段 的延长线与线段 交于点G . 当 时,是否存在点E , 使得 ?若存在,求出点E的坐标;若不存在,请说明理由.