湖南省郴州市2020年中考数学试卷
试卷更新日期:2020-08-12 类型:中考真卷
一、单选题
-
1. 如图表示互为相反数的两个点是( )
 A、点 与点 B、点 与点 C、点 与点 D、点 与点2. 年 月 日,北斗三号最后一颗全球组网卫星在西昌卫星发射中心点火升空.北斗卫星导航系统可提供高精度的授时服务,授时精度可达 纳秒( 秒= 纳秒)用科学记数法表示 纳秒为( )A、 秒 B、 秒 C、 秒 D、 秒3. 下列图形是中心对称图形的是( )A、
A、点 与点 B、点 与点 C、点 与点 D、点 与点2. 年 月 日,北斗三号最后一颗全球组网卫星在西昌卫星发射中心点火升空.北斗卫星导航系统可提供高精度的授时服务,授时精度可达 纳秒( 秒= 纳秒)用科学记数法表示 纳秒为( )A、 秒 B、 秒 C、 秒 D、 秒3. 下列图形是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,直线 被直线 所截下列条件能判定 的是( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,直线 被直线 所截下列条件能判定 的是( )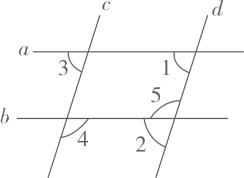 A、 B、 C、 D、6. 某鞋店试销一种新款男鞋,试销期间销售情况如下表:
A、 B、 C、 D、6. 某鞋店试销一种新款男鞋,试销期间销售情况如下表:鞋的尺码( )
销售数量(双)
则该组数据的下列统计量中,对鞋店下次进货最具有参考意义的是( )
A、中位数 B、平均数 C、众数 D、方差7. 如图 ,将边长为 的大正方形剪去一个边长为 的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图 所示长方形.这两个图能解释下列哪个等式( ) A、 B、 C、 D、8. 在平面直角坐标系中,点 是双曲线 上任意一点,连接 ,过点 作 的垂线与双曲线 交于点 ,连接 .已知 ,则 ( )
A、 B、 C、 D、8. 在平面直角坐标系中,点 是双曲线 上任意一点,连接 ,过点 作 的垂线与双曲线 交于点 ,连接 .已知 ,则 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若分式 的值不存在,则 .10. 已知关于 的一元二次方程 有两个相等的实数根,则 .11. 质检部门从 件电子元件中随机抽取 件进行检测,其中有 件是次品.试据此估计这批电子元件中大约有件次品.12. 某 人学习小组在寒假期间进行线上测试,其成绩(分)分别为: ,方差为 .后来老师发现每人都少加了 分,每人补加 分后,这 人新成绩的方差 .13. 小红在练习仰卧起坐,本月 日至 日的成绩与日期具有如下关系:
日期 (日)
成绩 (个)
小红的仰卧起坐成绩y与日期 之间近似为一次函数关系,则该函数表达式为 .
14. 在平面直角坐标系中,将 以点 为位似中心, 为位似比作位似变换,得到 .已知 ,则点 的坐标是 . 15. 如图,圆锥的母线长为 ,侧面展开图的面积为 ,则圆锥主视图的面积为 .
15. 如图,圆锥的母线长为 ,侧面展开图的面积为 ,则圆锥主视图的面积为 . 16. 如图,在矩形 中, .分别以点 为圆心,以大于 的长为半径画弧,两弧相交于点 和 .作直线 分别与 交于点 ,则 .
16. 如图,在矩形 中, .分别以点 为圆心,以大于 的长为半径画弧,两弧相交于点 和 .作直线 分别与 交于点 ,则 .
三、解答题
-
17. 计算:18. 解方程:19. 如图,在菱形 中,将对角线 分别向两端延长到点 和 ,使得 .连接 .求证:四边形 是菱形.
 20. 疫情期间,我市积极开展“停课不停学”线上教学活动,并通过电视、手机 等平台进行教学视频推送.某校随机抽取部分学生进行线上学习效果自我评价的调查(学习效果分为: .效果很好; .效果较好; .效果一般; .效果不理想)并根据调查结果绘制了如下两幅不完整的统计图:
20. 疫情期间,我市积极开展“停课不停学”线上教学活动,并通过电视、手机 等平台进行教学视频推送.某校随机抽取部分学生进行线上学习效果自我评价的调查(学习效果分为: .效果很好; .效果较好; .效果一般; .效果不理想)并根据调查结果绘制了如下两幅不完整的统计图: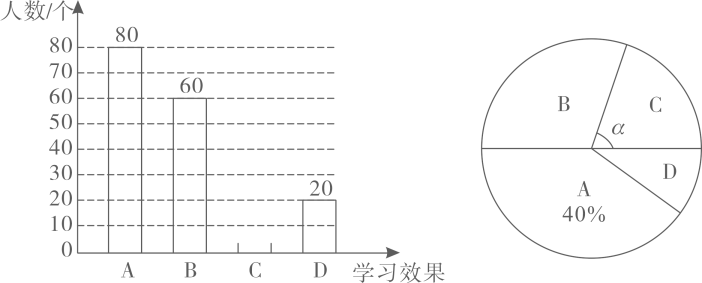 (1)、此次调查中,共抽查了-名学生;(2)、补全条形统计图,并求出扇形统计图中∠a的度数;(3)、某班 人学习小组,甲、乙 人认为效果很好,丙认为效果较好,丁认为效果一般.从学习小组中随机抽取 人,则“ 人认为效果很好, 人认为效果较好”的概率是多少?(要求画树状图或列表求概率)21. 2020年5月5日,为我国载人空间站工程研制的长征五号运较火箭在海南文昌首飞成功.运载火箭从地面 处发射、当火箭到达点 时,地面 处的雷达站测得 米,仰角为 .3秒后,火箭直线上升到达点 处,此时地面 处的雷达站测得 处的仰角为 .已知 两处相距 米,求火箭从 到 处的平均速度(结果精确到 米,参考数据: )
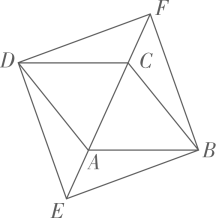
(1)、此次调查中,共抽查了-名学生;(2)、补全条形统计图,并求出扇形统计图中∠a的度数;(3)、某班 人学习小组,甲、乙 人认为效果很好,丙认为效果较好,丁认为效果一般.从学习小组中随机抽取 人,则“ 人认为效果很好, 人认为效果较好”的概率是多少?(要求画树状图或列表求概率)21. 2020年5月5日,为我国载人空间站工程研制的长征五号运较火箭在海南文昌首飞成功.运载火箭从地面 处发射、当火箭到达点 时,地面 处的雷达站测得 米,仰角为 .3秒后,火箭直线上升到达点 处,此时地面 处的雷达站测得 处的仰角为 .已知 两处相距 米,求火箭从 到 处的平均速度(结果精确到 米,参考数据: )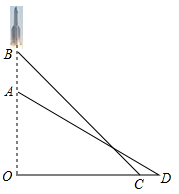 22. 为支援抗疫前线,某省红十字会采购甲、乙两种抗疫物资共 吨,甲物资单价为 万元/吨,乙物资单价为 万元吨,采购两种物资共花费 万元.(1)、求甲、乙两种物资各采购了多少吨?(2)、现在计划安排 两种不同规格的卡车共 辆来运输这批物资.甲物资 吨和乙物资 吨可装满一辆 型卡车;甲物资 吨和乙物资 吨可装满一辆 型卡车.按此要求安排 两型卡车的数量,请问有哪几种运输方案?23. 如图, 内接于⊙ , 是⊙ 的直径.直线 与⊙ 相切于点 ,在 上取一点 使得 .线段 , 的延长线交于点 .
22. 为支援抗疫前线,某省红十字会采购甲、乙两种抗疫物资共 吨,甲物资单价为 万元/吨,乙物资单价为 万元吨,采购两种物资共花费 万元.(1)、求甲、乙两种物资各采购了多少吨?(2)、现在计划安排 两种不同规格的卡车共 辆来运输这批物资.甲物资 吨和乙物资 吨可装满一辆 型卡车;甲物资 吨和乙物资 吨可装满一辆 型卡车.按此要求安排 两型卡车的数量,请问有哪几种运输方案?23. 如图, 内接于⊙ , 是⊙ 的直径.直线 与⊙ 相切于点 ,在 上取一点 使得 .线段 , 的延长线交于点 .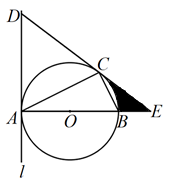 (1)、求证:直线 是⊙ 的切线;(2)、若 , ,求阴影部分的面积(结果保留 ).24. 为了探索函数 的图象与性质,我们参照学习函数的过程与方法.
(1)、求证:直线 是⊙ 的切线;(2)、若 , ,求阴影部分的面积(结果保留 ).24. 为了探索函数 的图象与性质,我们参照学习函数的过程与方法.列表:
描点:在平面直角坐标系中,以自变量 的取值为横坐标,以相应的函数值 为纵坐标,描出相应的点,如图 所示:
 (1)、如图 ,观察所描出点的分布,用一条光滑曲线将点顺次连接起来,作出函数图象;(2)、已知点 在函数图象上,结合表格和函数图象,回答下列问题:
(1)、如图 ,观察所描出点的分布,用一条光滑曲线将点顺次连接起来,作出函数图象;(2)、已知点 在函数图象上,结合表格和函数图象,回答下列问题:若 ,则 ;
若 ,则 ;
若 ,则 (填“>”,“=”,“<”).
(3)、某农户要建造一个图 所示的长方体形无盖水池,其底面积为 平方米,深为 米.已知底面造价为 千元/平方米,侧面造价为 千元/平方米,设水池底面一边的长为 米,水池总造价为 千元.①请写出 与 的函数关系式;
②若该农户预算不超过 千元,则水池底面一边的长 应控制在什么范围内?
25. 如图 ,在等腰直角三角形 中, .点 是 的中点,以 为边作正方形 ,连接 .将正方形 绕点 顺时针旋转,旋转角为 .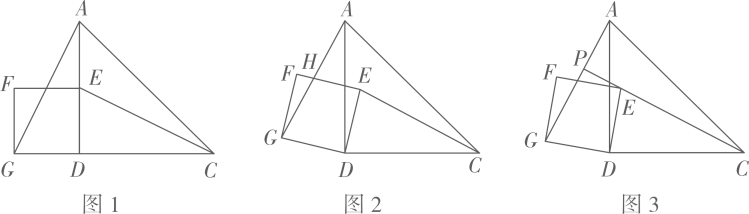 (1)、如图 ,在旋转过程中,
(1)、如图 ,在旋转过程中,①判断 与 是否全等,并说明理由;
②当 时, 与 交于点 ,求 的长.
(2)、如图 ,延长 交直线 于点 .①求证: ;
②在旋转过程中,线段 的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
26. 如图 ,抛物线 与 轴交于 ,与 轴交于点 .已知直线 过 两点.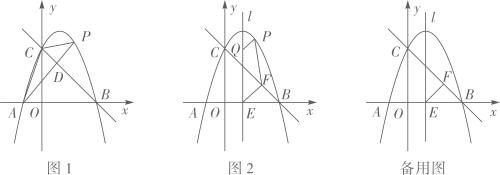 (1)、求抛物线和直线 的表达式;(2)、点 是抛物线上的一个动点,
(1)、求抛物线和直线 的表达式;(2)、点 是抛物线上的一个动点,①如图 ,若点 在第一象限内,连接 ,交直线 于点 .设 的面积为 , 的面积为 ,求 的最大值;
②如图2,抛物线的对称轴 与 轴交于点 ,过点 作 ,垂足为 .点 是对称轴 上的一个动点,是否存在以点 为顶点的四边形是平行四边形?
若存在,求出点 的坐标;若不存在,请说明理由.