广东省2020年中考数学试卷
试卷更新日期:2020-08-12 类型:中考真卷
一、单选题
-
1. 9的相反数是( )A、 B、 C、 D、2. 一组数据2,4,3,5,2的中位数是( )A、5 B、35 C、3 D、253. 在平面直角坐标系中,点 关于 轴对称的点的坐标为( )A、 B、 C、 D、4. 若一个多边形的内角和是540°,则该多边形的边数为( )A、4 B、5 C、6 D、75. 若式子 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、6. 已知 的周长为16,点 , , 分别为 三条边的中点,则 的周长为( )A、8 B、 C、16 D、47. 把函数 的图象向右平移1个单位长度,平移后图象的函数解析式为( )A、 B、 C、 D、8. 不等式组 的解集为( )A、无解 B、 C、 D、9. 如图,在正方形 中, ,点 , 分别在边 , 上, .若将四边形 沿 折叠,点 恰好落在 边上,则 的长度为( )
 A、1 B、 C、 D、210. 如图,抛物线 的对称轴是 .下列结论:① ;② ;③ ;④ ,正确的有( )
A、1 B、 C、 D、210. 如图,抛物线 的对称轴是 .下列结论:① ;② ;③ ;④ ,正确的有( )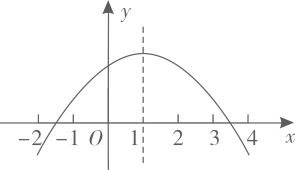 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
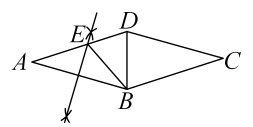
11. 分解因式:xy―x= .12. 若 与 是同类项,则 .13. 若 ,则 .14. 已知 , ,计算 的值为 .15. 如图,在菱形 中, ,取大于 的长为半径,分别以点 , 为圆心作弧相交于两点,过此两点的直线交 边于点 (作图痕迹如图所示),连接 , ,则 的度数为 .
 16. 如图,从一块半径为 的圆形铁皮上剪出一个圆周角为120°的扇形 ,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为 .
16. 如图,从一块半径为 的圆形铁皮上剪出一个圆周角为120°的扇形 ,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为 .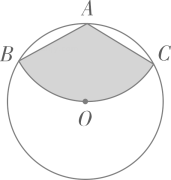 17. 有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, ,点 , 分别在射线 , 上, 长度始终保持不变, , 为 的中点,点 到 , 的距离分别为4和2.在此滑动过程中,猫与老鼠的距离 的最小值为 .
17. 有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, ,点 , 分别在射线 , 上, 长度始终保持不变, , 为 的中点,点 到 , 的距离分别为4和2.在此滑动过程中,猫与老鼠的距离 的最小值为 .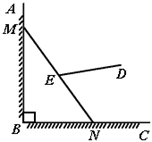
三、解答题(一)
-
18. 先化简,再求值: ,其中 , .19. 某中学开展主题为“垃圾分类知多少”的调查活动,调查问卷设置了“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,要求每名学生选且只能选其中一个等级.随机抽取了120名学生的有效问卷,数据整理如下:
等级
非常了解
比较了解
基本了解
不太了解
人数(人)
24
72
18
(1)、求 的值;(2)、若该校有学生1800人,请根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有多少人?20. 如图,在 中,点 , 分别是 、 边上的点, , , 与 相交于点 ,求证: 是等腰三角形.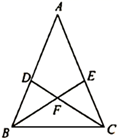
四、解答题(二)
-
21. 已知关于 , 的方程组 与 的解相同.(1)、求 , 的值;(2)、若一个三角形的一条边的长为 ,另外两条边的长是关于 的方程 的解.试判断该三角形的形状,并说明理由.22. 如图1,在四边形 中, , , 是 的直径, 平分 .
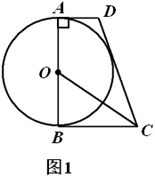 (1)、求证:直线 与 相切;(2)、如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.
(1)、求证:直线 与 相切;(2)、如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.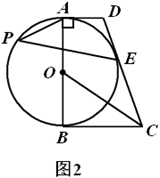 23. 某社区拟建 , 两类摊位以搞活“地摊经济”,每个 类摊位的占地面积比每个 类摊位的占地面积多2平方米,建 类摊位每平方米的费用为40元,建 类摊位每平方米的费用为30元,用60平方米建 类摊位的个数恰好是用同样面积建 类摊位个数的 .(1)、求每个 , 类摊位占地面积各为多少平方米?(2)、该社拟建 , 两类摊位共90个,且 类摊位的数量不少于 类摊位数量的3倍.求建造这90个摊位的最大费用.
23. 某社区拟建 , 两类摊位以搞活“地摊经济”,每个 类摊位的占地面积比每个 类摊位的占地面积多2平方米,建 类摊位每平方米的费用为40元,建 类摊位每平方米的费用为30元,用60平方米建 类摊位的个数恰好是用同样面积建 类摊位个数的 .(1)、求每个 , 类摊位占地面积各为多少平方米?(2)、该社拟建 , 两类摊位共90个,且 类摊位的数量不少于 类摊位数量的3倍.求建造这90个摊位的最大费用.五、解答题(三)
-
24. 如图,点 是反比例函数 ( )图象上一点,过点 分别向坐标轴作垂线,垂足为 , ,反比例函数 ( )的图象经过 的中点 ,与 , 分别相交于点 , .连接 并延长交 轴于点 ,点 与点 关于点 对称,连接 , .
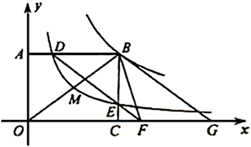 (1)、填空: ;(2)、求 的面积;(3)、求证:四边形 为平行四边形.25. 如图,抛物线 与 轴交于 , 两点,点 , 分别位于原点的左、右两侧, ,过点 的直线与 轴正半轴和抛物线的交点分别为 , , .
(1)、填空: ;(2)、求 的面积;(3)、求证:四边形 为平行四边形.25. 如图,抛物线 与 轴交于 , 两点,点 , 分别位于原点的左、右两侧, ,过点 的直线与 轴正半轴和抛物线的交点分别为 , , . (1)、求 , 的值;(2)、求直线 的函数解析式;(3)、点 在抛物线的对称轴上且在 轴下方,点 在射线 上,当 与 相似时,请直接写出所有满足条件的点 的坐标.
(1)、求 , 的值;(2)、求直线 的函数解析式;(3)、点 在抛物线的对称轴上且在 轴下方,点 在射线 上,当 与 相似时,请直接写出所有满足条件的点 的坐标.