浙江省杭州市2016-2017学年高二下学期数学期末考试试卷

试卷更新日期：2017-09-23 类型：期末考试

进入出卷网下载

一、选择题

1. 设集合A={x|x≤3，x∈N^*}，B={﹣2，0，2，3}，则A∩B=（）

A、{3} B、{2，3} C、{0，2，3} D、{﹣2，0，2}

查看试题解析
2. 设d为点P（1，0）到直线x﹣2y+1=0的距离，则d=（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{3 \sqrt{5}}{5}$ D、 $\frac{4 \sqrt{5}}{5}$

查看试题解析
3. 设向量 $\vec{a}$ =（﹣1，﹣1，1）， $\vec{b}$ =（﹣1，0，1），则cos＜ $\vec{a}$ ， $\vec{b}$ ＞=（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{6}}{3}$

查看试题解析
4. 下列四个图形中，不是以x为自变量的函数的图象是（）

A、 B、 C、 D、

查看试题解析
5. sin15°cos15°=（）

A、 $\frac{1}{4}$ B、 $\frac{\sqrt{3}}{4}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
6. 函数f（x）=ln（x²﹣x）的定义域为（　　）

A、（0，1） B、[0，1] C、（﹣∞，0）∪（1，+∞） D、（﹣∞，0]∪[1，+∞）

查看试题解析
7. 若l，m是两条不同的直线，α是一个平面，则下列命题正确的是（）

A、若l∥α，m∥α，则l∥m B、若l⊥m，m⊂α，则l⊥α C、若l∥α，m⊂α，则l∥m D、若l⊥α，l∥m，则m⊥α

查看试题解析
8. 若x∈R，则“x＞1”是“ $\frac{1}{x} < 1$ ”的（）

A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既非充分也非必要条件

查看试题解析
9. 下列函数是奇函数的是（）

A、f（x）=x²+2|x| B、f（x）=x•sinx C、f（x）=2^x+2^﹣^x D、 $f (x) = \frac{c o s x}{x}$

查看试题解析
10. 圆（x+2）²+y²=4与圆（x﹣2）²+（y﹣1）²=9的位置关系为（）

A、内切 B、相交 C、外切 D、相离

查看试题解析
11. 若实数x，y满足不等式组 ${\begin{matrix} x - y + 2 \geq 0 \\ x + y - 4 \leq 0 \\ y \geq 2 \end{matrix}$ ，则z=2x﹣y的最小值等于（）

A、﹣1 B、1 C、2 D、﹣2

查看试题解析
12. 在正方体ABCD﹣A₁B₁C₁D₁中，O、O₁分别为底面ABCD和A₁B₁C₁D₁的中心，以OO₁所在直线为轴旋转线段BC₁形成的几何体的正视图为（）

A、 B、 C、 D、

查看试题解析
13. 设函数f（x）=x²+bx+c（b，c∈R），若0≤f（1）=f（2）≤10，则（）

A、0≤c≤2 B、0≤c≤10 C、2≤c≤12 D、10≤c≤12

查看试题解析
14. 已知平行四边形ABCD的对角线相交于点O，点P在△COD的内部（不含边界）．若 $\vec{A P}$ =x $\vec{A B}$ +y $\vec{A D}$ ，则实数对（x，y）可以是（）

A、（ $\frac{1}{3}$ ， $\frac{2}{3}$ ） B、（ $\frac{1}{4}$ ，﹣ $\frac{3}{4}$ ） C、（ $\frac{3}{5}$ ， $\frac{1}{5}$ ） D、（ $\frac{3}{7}$ ， $\frac{5}{7}$ ）

查看试题解析
15. 设A，B是函数f（x）=sin|ωx|与y=﹣1的图象的相邻两个交点，若|AB|_min=2π，则正实数ω=（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{3}{2}$ D、2

查看试题解析
16. 设函数f（x）=2017x+sin²⁰¹⁷x，g（x）=log₂₀₁₇x+2017^x ，则（）

A、对于任意正实数x恒有f（x）≥g（x） B、存在实数x₀ ，当x＞x₀时，恒有f（x）＞g（x） C、对于任意正实数x恒有f（x）≤g（x） D、存在实数x₀ ，当x＞x₀时，恒有f（x）＜g（x）

查看试题解析
17. 设F为双曲线 $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的右焦点，过点F的直线分别交两条渐近线于A，B两点，OA⊥AB，若2|AB|=|OA|+|OB|，则该双曲线的离心率为（）

A、 $\sqrt{3}$ B、2 C、 $\frac{\sqrt{5}}{2}$ D、 $\sqrt{5}$

查看试题解析
18. 设点P在△ABC的BC边所在的直线上从左到右运动，设△ABP与△ACP的外接圆面积之比为λ，当点P不与B，C重合时，（）

A、λ先变小再变大 B、当M为线段BC中点时，λ最大 C、λ先变大再变小 D、λ是一个定值

查看试题解析

二、填空题

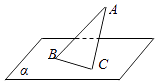
19. 设抛物线x²=4y，则其焦点坐标为，准线方程为．

查看试题解析
20. 在平行四边形ABCD中，AD= $\sqrt{2}$ ，AB=2，若 $\vec{B F}$ = $\vec{F C}$ ，则 $\vec{A F}$ • $\vec{D F}$ = ．

查看试题解析
21. 设数列{a_n}的前n项和为S_n ．若S_n=2a_n﹣n，则 $\frac{2}{a_{1} a_{2}}$ + $\frac{4}{a_{2} a_{3}}$ + $\frac{8}{a_{3} a_{4}}$ + $\frac{16}{a_{4} a_{5}}$ = ．

查看试题解析
22. 在△ABC中，∠ABC= $\frac{π}{3}$ ，边BC在平面α内，顶点A在平面α外，直线AB与平面α所成角为θ．若平面ABC与平面α所成的二面角为 $\frac{π}{3}$ ，则sinθ= ．

查看试题解析

三、解答题

23. 设A是单位圆O和x轴正半轴的交点，P，Q是圆O上两点，O为坐标原点，∠AOP= $\frac{π}{6}$ ，∠AOQ=α，α∈[0， $\frac{π}{2}$ ]．

(1)、若Q（ $\frac{3}{5}$ ， $\frac{4}{5}$ ），求cos（α﹣ $\frac{π}{6}$ ）的值；

(2)、设函数f（α）=sinα•（ $\vec{O P}$ • $\vec{O Q}$ ），求f（α）的值域．

查看试题解析
24. 如图，P是直线x=4上一动点，以P为圆心的圆Γ经定点B（1，0），直线l是圆Γ在点B处的切线，过A（﹣1，0）作圆Γ的两条切线分别与l交于E，F两点．

(1)、求证：|EA|+|EB|为定值；

(2)、设直线l交直线x=4于点Q，证明：|EB|•|FQ|=|BF•|EQ|．

查看试题解析
25. 设函数f（x）= $\sqrt{1 - x^{2}}$ ，g（x）=a（x+b）（0＜a≤1，b≤0）．

(1)、讨论函数y=f（x）•g（x）的奇偶性；

(2)、当b=0时，判断函数y= $\frac{g (x)}{f^{2} (x)}$ 在（﹣1，1）上的单调性，并说明理由；

(3)、设h（x）=|af²（x）﹣ $\frac{g (x)}{a}$ |，若h（x）的最大值为2，求a+b的取值范围．

查看试题解析