2021高考一轮复习 第二十九讲 直线与圆、圆与圆的位置关系
试卷更新日期:2020-08-12 类型:一轮复习
一、单选题
-
1. 已知圆 ,过点(1,2)的直线被该圆所截得的弦的长度的最小值为( )A、1 B、2 C、3 D、42. 圆C的半径为5,圆心在x轴的负半轴上,且被直线 截得的弦长为6,则圆C的方程为( )A、 B、 C、 D、3. 圆 关于直线 ( )对称,则 的最小值是( )A、 B、 C、 D、4. 圆 与圆 的公切线共有( )A、1条 B、2条 C、3条 D、4条5. 已知直线 过圆 的圆心,则 的最小值为( )A、3 B、 C、6 D、6. 过点A(1,2)作圆x2+(y﹣1)2=1的切线,则切线方程是( )A、x=1 B、y=2 C、x=2或y=1 D、x=1或y=27. 已知圆 截直线 所得线段的长度是 ,则圆M与圆N:(x-1)2+(y-1)2=1的位置关系是( )A、内切 B、相交 C、外切 D、相离8. 过点 作圆 的两条切线,切点分别为 ,则直线 的方程为( )A、 B、 C、 D、9. 过点 的直线与圆 有两个交点A和B,它们与原点O确定的三角形OAB的面积最大值是( )A、 B、1 C、 D、210. 从点 向圆 引切线,则切线长的最小值为( )A、4 B、 C、5 D、11. 直线 与曲线 有两个不同的交点,则实数k的取值范围是( )A、 B、 C、 D、12. 圆 上到直线 的距离为 的点共有( )A、 个 B、 个 C、 个 D、 个
二、多选题
-
13. 在同一直角坐标系中,直线 与圆 的位置可能是( )A、
 B、
B、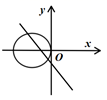 C、
C、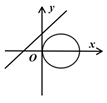 D、
D、 14. 已知圆 上存在两个点到点 的距离为 ,则m的可能的值为( )A、1 B、-1 C、-3 D、-515. 若圆 与圆 相切,则m的值可以是( )A、 B、 C、 D、
14. 已知圆 上存在两个点到点 的距离为 ,则m的可能的值为( )A、1 B、-1 C、-3 D、-515. 若圆 与圆 相切,则m的值可以是( )A、 B、 C、 D、三、填空题
-
16. 设直线l:y=kx+b(k>0),圆C1:x2+y2=1,C2:(x﹣4)2+y2=1,若直线l与C1 , C2都相切,则k=;b= .17. 过点 且倾斜角为 的直线l与圆 相交的弦长为 .18. 在平面直角坐标系xOy中,过点P(2,﹣6)作直线交圆O:x2+y2=16于A , B两点, C( , )为弦AB的中点,则 的取值范围是 .19. 圆 与圆 的公共弦的长为 .20. 关于 的方程 有两个不同的实数解时,实数k的取值范围是
四、解答题